Задание нечетких множеств.

Понятие нечеткого множества. Функции принадлежности. Задание нечетких множеств. Операции над нечеткими множествами.

Задание нечетких множеств.

Зададим принадлежность элемента 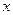ко множеству 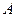с помощью характеристической функции:

.

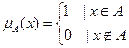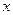Представим, что характеристическая функция может принимать любое значение в интервале . Т. о. элемент множества 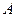может быть любым элементом в небольшой степени близким к 0 или в небольшой степени близким к 1.

Пусть 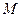– множество, 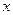– элемент множества 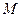, тогда нечеткое подмножество 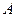множества 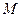определяется, как множество упорядоченных пар , где 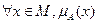–характеристическая функция принадлежности, принимающая свои значения на упорядоченном множестве , которое указывает степень или уровень принадлежности элемента 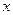к подмножеству 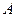. Множество – множество принадлежности. Если 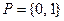, то нечеткое подмножество 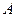рассматривают как обычное подмножество.

Пример 1: нечёткое подмножество чисел 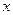, приблизительно равных данному действительному числу 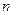, где , 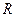– множество действительных чисел.

Пример 2: нечёткое подмножество целых чисел близких к нулю.

Подмножество 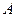принадлежит подмножеству 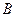( 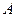содержится в 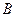), если : .

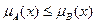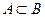Строгое включение соответствует случаю, когда, по крайней мере, одно неравенство строгое: .

Подмножества 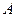и 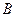равны тогда и только тогда, когда : .

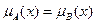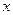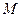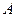Если найдется, по крайней мере, один такой элемент из , что , то говорят, что подмножества и 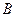не равны: .