Операции над нечеткими множествами.
1. Дополнение.
Пусть 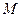 – множество,
– множество, 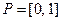 – множество принадлежности,
– множество принадлежности, 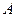 и
и 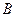 – нечеткие подмножества. Говорят, что A и B дополняют друг друга, если
– нечеткие подмножества. Говорят, что A и B дополняют друг друга, если 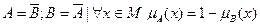 .
.
Имеет место закон двойного дополнения: 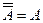 .
.
Для нечетких множеств можно построить визуальное представление в следующем виде:
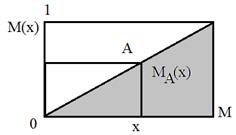
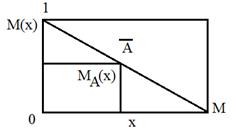
При визуальном представлении используется прямоугольная система координат. Прямоугольная система координат, на оси ординат которой откладывается 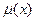 , а на оси абсцисс в произвольном порядке расположены элементы
, а на оси абсцисс в произвольном порядке расположены элементы 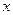 множества
множества 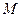 . Принадлежность каждого элемента определяется величиной его ординаты. Заштрихованная часть в первом случае изображает подмножество
. Принадлежность каждого элемента определяется величиной его ординаты. Заштрихованная часть в первом случае изображает подмножество 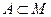 .
.
Пример:
пусть 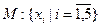 ,
, 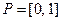 ,
, 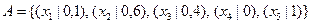 .
.
Тогда 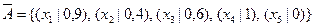 .
.
2. Пересечение.
Пусть 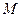 – множество,
– множество, 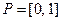 – множество принадлежности,
– множество принадлежности, 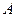 и
и 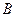 – нечеткие подмножества. Пересечение
– нечеткие подмножества. Пересечение 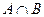 определяют, как наибольшее нечеткое подмножество, содержащее одновременно
определяют, как наибольшее нечеткое подмножество, содержащее одновременно 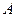 и
и 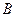 :
: 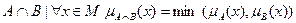 .
.

Пример:
пусть 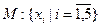 ,
, 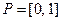 ,
, 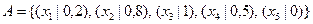 ,
, 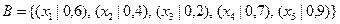 .
.
Тогда 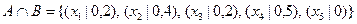 .
.
3. Объединение.
Пусть 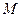 – множество,
– множество, 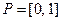 – множество принадлежности,
– множество принадлежности, 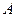 и
и 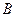 – нечеткие подмножества. Определим объединение
– нечеткие подмножества. Определим объединение 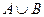 , как множество, которое содержит
, как множество, которое содержит 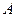 и
и 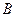 :
: 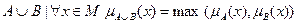 .
.

Пример:
пусть 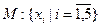 ,
, 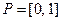 ,
, 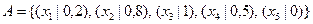 ,
, 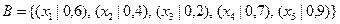 .
.
Тогда 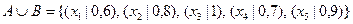 .
.
4. Разность.
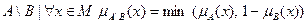 или
или 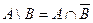 .
.
Пример:
пусть 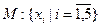 ,
, 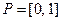 ,
, 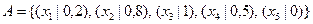 ,
, 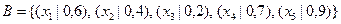 .
.
Тогда 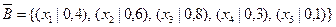 ,
,
а 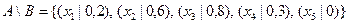 .
.
Введенные операции удовлетворяют тем же законам, что и те же операции для множеств.
1. Закон коммутативности:
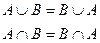
2. Закон ассоциативности:
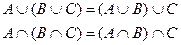
3. Закон идемпотентности:
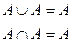
4. Закон дистрибутивности:
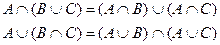
5. Действия с константами.:
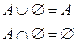
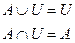
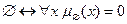
6. Закон двойного дополнения:
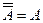
7. Законы де Моргана:
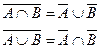
8. Законы поглощения:
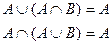
Дата добавления: 2015-12-16; просмотров: 727;
