Арифметические операции над нечеткими интервалами
В обобщенном виде:
S1*S2=(U1*U2 / U1 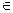 S1, U2
S1, U2 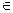 S2, *:={ . , +, -, /})
S2, *:={ . , +, -, /})
Сложение:
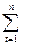 μSt=μS, где S={
μSt=μS, где S={ 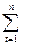 Ŝt ,
Ŝt , 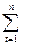 Št , (
Št , ( 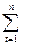 l t-1)-1 , (
l t-1)-1 , ( 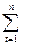 r t-1)-1}
r t-1)-1}
если 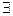 t , такое что l t=1 то (
t , такое что l t=1 то ( 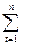 l t-1)-1=1 и аналогично
l t-1)-1=1 и аналогично
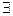 t , такое что r t=1 то (
t , такое что r t=1 то ( 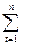 r t-1)-1=1
r t-1)-1=1
для линейных интервалов:
S={ 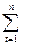 Ŝt ,
Ŝt , 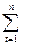 Št ,
Št , 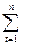 αt ,
αt , 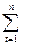 βt }
βt }
Вычитание:
μS= μS1 - μS2 , здесь
Sн={Ŝ1-Š2; Š1-Ŝ2; (l 1-1- r 2-1)-1; (r 1-1- l 2-1)-1}
Sн – нелинейное
В случае линейных интервалов
Sл={Ŝ1-Š2; Š1-Ŝ2; α1+β2; β1+α2}
Умножение:
μS= 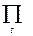 μSt , где
μSt , где
Sн={ 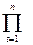 Ŝt;
Ŝt; 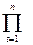 Št; (
Št; ( 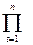 l t-1)-1; (
l t-1)-1; ( 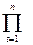 r t-1)-1}
r t-1)-1}
Sл={ 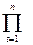 Ŝt;
Ŝt; 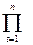 Št;
Št; 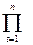 αt ;
αt ; 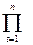 βt }
βt }
Деление:
μS= μS1 / μS2 , где
Sн={Ŝ1/Š2; Š1/Ŝ2; (l 1-1/ r 2-1)-1; (r 1-1/ l 2-1)-1}
Sл={Ŝ1/Š2; Š1/Ŝ2; α1/β2; β1/α2}
Приведенные выше формулы (через обратные функции) позволяют для ряда стандартных функций принадлежности получить точные результаты не прибегая к численным методам решения нелинейных уравнений. При этом в общем случае формулы определены для функций l и r представленных разными выражениями, кроме того нет необходимости в апроксимации левых и правых ветвей функции принадлежности одной монотонно возрастающей функции.
Пример:
S1={ln 2 +4; 9; eu-4-1; 1- 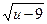 }
}
S2={ln 2 +2; 8; eu-2-1; -0,25u+3}
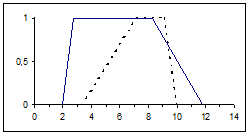 |
l1=eu-4-1; l1-1=ln(u+1)+4
l2=eu-2-1; l2-1=ln(u+1)+2
l1-1+ l2-1=2ln(u+1)+6;
(l1-1+ l2-1)-1=(eu-6)1/2-1
r1=1- 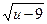 ; r1-1=(1-u)2+9
; r1-1=(1-u)2+9
r2=-0,25u+3; r2-1=4(3-u)
r1-1+ r2-1=1-2u+u2+9+12-4u=u2-6u+22;
(r1-1+ r2-1)-1=3± 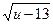
Š1+Š2=9+8=17; r=3- 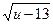
u>17 3+ 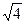 =3+2=5 не может быть так как r меняется от 0 до 1
=3+2=5 не может быть так как r меняется от 0 до 1
Ŝ1+Ŝ2=ln2+4+ln2+2=2ln2+6
S1+S2={2ln2+6; 17; (eu-6)1/2-1; 3- 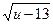 }
}
Пример 2: S1={Ŝ1, Š1, α1, β1}={3, 5, 2, 4}
S2={Ŝ2, Š2, α2, β2}={10, 11, 4, 2}
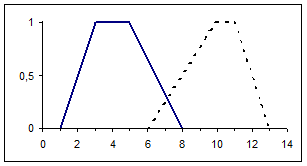 |
l1=1/2(x-1/2)
r1=-1/4x+9/4
l2=1/4x-3/2
r2=-1/2x+13/2
l1-1=2x+1
r1-1=-4x+9
l2-1=4x+6
r2-1=-13-2x
S– ={ Ŝ1-Š2; Š1-Ŝ2; (l 1-1- r 2-1)-1; (r 1-1- l 2-1)-1}={-8; -5; 1/4x+3; 3/8-1/8x}
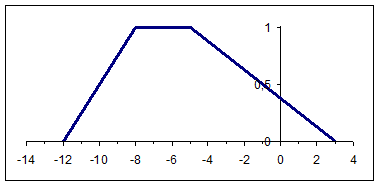
Коментарии: в литературе показано, что результат сложения и вычитания LR – нечетких чисел есть также нечеткое число (а±в, αа+αв, βа+βв), в то же время результат умножения и деления может быть получен приближенно ≈(ав, аαв+вαа, аβв+вβа)
≈(а/в, (аβв+вαа)/в2, (аαв+вβа)/в2)
Нечеткое число А+(- А)≠0
А.(1/А) ≠1
Следовательно, вытекает необходимость разработки специальных алгаритмов.
Рассмотрим алгаритм выполнения нечетких операций на основе теоремы о декомпозиции, то есть с использование разложения на α уровневые нечеткие подмножества.
А=αАα
Аα – четкое подмножество
Аα= {а: mА(а)≥0}
αАα :=(α, а)
Доказано следующее утверждение: Для любой непрерывной функции f: R 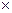 R
R 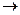 R высказывание (
R высказывание ( 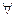 α
α 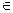 [0,1])[f(A,B)│α=f(Aα, Bα)] справедливо тогда и только тогда если выполняются следующие условия:
[0,1])[f(A,B)│α=f(Aα, Bα)] справедливо тогда и только тогда если выполняются следующие условия:
1. если дополнение носителей SA, SB компактны
2. функции принадлежности mА(а), mВ(в) полунепрерывны сверху и должны быть нормальными
При этих условиях:
(А+В)α=Аα+Вα
(А .В)α=Аα .Вα
Дата добавления: 2016-01-09; просмотров: 1302;
