Арифметические действия в двоичной и десятичной
системах счисления[5, 15]
Числа в ЭВМ представляются в двоичной форме, в этой же форме выполняются и все 4 арифметических действия. Правила работы многоразрядных чисел в двоичной системе точно такие же, как и в десятичной, только 10 заменяется на 2.
Рассмотрим процесс сложения двух чисел:
|
2481
Выполняем действия справа налево в следующем порядке:
1) 3 плюс 1 равно 4;
2) 4 плюс 8 равно 12. Записываем 2 и переносим 1,
3) 1 плюс 5 плюс 4 равно 10. Записываем 0, переносим 1;
4) 1 плюс 6 плюс 2 равно 9.
Для выполнения 4 арифметических действий в любой системе счисления необходимо знать таблицы сложения, вычитания и умножения. Каждая из них состоит из 4 строк:
0+0 = 0 0−0 = 0 0×0 = 0
0+1 = 1 1−0 = 1 0×1 = 0
1+0 = 1 1−1 = 0 1×1 = 0
1+1 = 10 10−1 = 1 1×1 = 1
Операции с делением двоичных чисел происходят с использованием двоичных таблиц умножения и вычитания. Сложение в двоичной форме выполняются следующим образом:
|
110
Точно так же выполняем действия справа налево:
1) 0 плюс 0 равно 0;
2) 1 плюс 1 равно 10 (напоминаю, что 2 в двоичной системе представляется как 10). Записываем 0 и переносим 1;
3) 1 плюс 0 плюс 1 равно 10. Записываем 0 и переносим 1;
4) 1 плюс 1 равно 10. Поскольку это последнее действие, записываем 10. Точно так же, как сделали бы это в десятичной системе.
В примере стрелками (↓) показаны единицы переноса в старшие разряды. Для проверки правильности результата выполним следующее десятичное сложение: 10+6 = 16;
Преобразовав все эти три числа в двоичной форме, вместо 10(10) получим
1010(2), вместо 6−110(2) и вместо 16−10000(2) .
Следует заметить, что десятичное число можно иногда спутать с двоичным.
Выполняя сложение 10+6 = 16, мы предполагаем, что число 10 десятичное, а не двоичное. Чтобы не было путаницы, можно число заключить в скобки и приписать ему в виде индекса основание системы счисления − 10, а не 2, тогда 10(2) обозначает двоичное число 10, а 10(10) – десятичное.
Правила вычитания также одинаковы в двоичной и десятичной системах счисления.
Рассмотрим пример вычитания 174 и 197:
|
174
В двоичной форме вычитание представлено в следующем виде:
|
10101110
где: 00010111 = (1×24) + (0×23) + (1×22) + (1×21) + (1×20) = 16+0 + 4 + 2 + 1 = = 23(10), что абсолютно верно. Проверить правильность можно обратным действием, то есть сложением:
|
10101110
Умножение двоичных чисел производится с использованием умножения и сложения.
Пример умножения 23,625 на 2,75:
где: 23,625(10) = (1×24) + (0×22) + (1×21) + (1×20) + (1×2−1) + (0×2−2) + (1×2−3) = = 10111,101(2) .
Число 275 переводится аналогичным способом:
|
10,11
|
1011101
111111,111
Деление двоичных чисел происходит с использованием двоичных таблиц умножения и вычитания.
Пример деления 430 на 10
|
 110101110 1010
110101110 1010
1010 101011(2)
|
1010
|
1010
|
1010
Из приведенных примеров видно, что правила выполнения арифметических действий в десятичной и двоичной системах одинаковы. Причем в двоичной системе арифметические действия выполняются гораздо проще.
Двоичная система счисления[5, 15]
Как известно, современные компьютеры состоят из электронных схем, которые могут находиться в одном из двух состояний, определяемых протеканием электрического тока.
Состояние электронной схемы, в которой протекает электрический ток, условно кодируется – 1, а противоположное состояние – 0.
Можно кодировать состояние электронной схемы по уровню напряжения на ее входах или выходах: высокий уровень напряжения – 1, низкий уровень напряжения – 0.
Транзистор может либо проводить электрический ток (транзистор открыт), либо не проводить (транзистор заперт), магнитная поверхность может быть либо намагничена, либо размагничена и т.д.
Одно из устойчивых состояний элемента соответствует цифре 0, а другое – цифре 1. В этом отношении двоичная система счисления имеет преимущества перед остальными системами и поэтому оказывается очень удобной для ее применения в вычислительных машинах.
В двоичной системе легко реализуются арифметические операции, что дает возможность значительно упростить конструкции вычислительных устройств по сравнению с устройствами, работающими в других системах. Числа в двоичную систему счисления могут быть переведены различными способами, один из которых – табличный. Его сущность заключается в том, что число представляется в виде суммы степеней оснований системы счисления 2 с соответствующими коэффициентами.
Так, число N может быть представлено в виде следующей суммы:
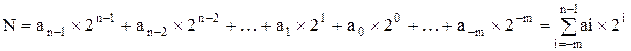
Где коэффициенты ai при степенях основания могут принимать только 2 значения: 0 или 1.
Двоичные числа – это числа, состоящие только из единиц и нулей.
Двоичные числа можно рассматривать как некоторый код, вроде кода для секретных сообщений. Так число 111 представляет собой код числа 7; 1001 есть код числа 9.
Обычные числа, такие как 7 или 9, называют десятичными числами. Известная нам все десятичная система позволяет выразить числовые значения с помощью нескольких цифр (разрядов). Так,
3456(10) = 3000 + 400 + 50 + 6 = (3×1000) + (4×100) + (5×10) + 6 =
= (3×103) + (4×102) + (5×101) + (6×100) = 3456(10)
где показатели степени 10 расположены в порядке убывания (вспомним, что 101 = 10 и 100 = 1).
Двоичная система отличается от десятичной тем, что основание 10 заменяется на основание 2. Так в двоичной системе:
1001(2) = (1×23) + (0×22) + (0×21) + (1×20) = (1×8) + (0×4) + (0×2) + (1×1) =
= 8 + 1 = 9(10)
В таблице 3 представлены 16 двоичных чисел (вместе с 0).
Таблица 3
Первые 16 двоичных чисел
| Числа десятичные | Числа двоичные |
Нахождение двоичного кода для десятичного числа называется преобразованием числа из десятичной системы в двоичную. Обратное преобразование десятичных чисел в двоичные производится непрерывным делением преобразуемого числа на 2 с одновременным слежением за получающимися остатками.
Например:
 9:2 = 4 остаток 1
9:2 = 4 остаток 1
 4:2 = 2 остаток 0
4:2 = 2 остаток 0
 2:2 = 1 остаток 0
2:2 = 1 остаток 0
 1:2 = 0 остаток 1
1:2 = 0 остаток 1
1 0 0 1
Таким образом, 9(10) = 1001(2), потому что
1001(2) = (1×23) + (0×22) + (0×21) + (1×20) = 8 + 1 = 9(10)
Существует более сложный способ преобразования числа из десятичной системы в двоичную.
Чтобы выполнить такое преобразование, мы должны найти наибольшую степень двух, которая не превышает преобразуемое число. Возьмем, например, число 1600. Наибольшая степень 2, не превышающая 1600, есть 1024 (см. табл. 4).
Таблица 4
Степени 2
| X | |
Рассмотрим теперь каждую степень 2 в последовательности от 1024 до 1. Будем по очереди вычитать их, следя за тем, чтобы результат не получился отрицательным. Каждый раз, когда вычитание степени 2 возможно, записываем 1 в двоичное число.
Каждый раз, когда вычитание степени 2 невозможно, записываем 0.
|
1024
|
512
(256) 0
(128) 0
|
64 1
(32) 0
(16) 0
(8) 0
(4) 0
(2) 0
(1) 0
Ответ: 11001000000(2) = 1600(10)
Таким образом, прочитав результаты сверху вниз, в данном случае получим число: 11001000000(2).
Нахождение десятичного числа по его двоичному коду называется преобразованием из двоичной формы в десятичную. Такие преобразования выполняются довольно просто. Выпишем двоичные цифры преобразуемого числа, так как показано ниже, и под каждой цифрой, начиная с самой первой, напишем последовательные степени 2, взятые из предыдущего примера. Теперь сложим те степени 2, которые написаны над 1 в двоичном числе. Отсюда видно, что число, которое мы ранее преобразовывали в двоичную форму, теперь преобразовано назад в десятичную.
1024 512 256 128 64 32 16 8 4 2 1
1 1 0 0 1 0 0 0 0 0 0
1024 + 512 + 64 = 1600(10)
Двоичный разряд носит название БИТ (1 или 0). Так двоичное число 11001000000 занимает 11 БИТ.
Шестнадцатеричная система[5]
Вспомним, что 2 – это основание двоичной системы. Это означает, что при записи любого числа используются всего две цифры − 0 и 1 и степени 2. Аналогично 10 – основание десятичной системы. Например, 5(10) = 101(2). Имеются и другие системы с основаниями, отличными от 2 и 10. Чаще других используется шестнадцатеричная система счисления с основанием 16.
В шестнадцатеричной системе используются 16 цифр – 0, 1, 2, …, 9, A, B, C, D, E и F. Числа в шестнадцатеричной системе образуются так же, как и в десятичной, но вместо 10 используется 16. Так, если в десятичной системе мы имеем:
3 × 103
3456 = + 4 × 102 = 3 × 103 + 4 × 102 + 5 × 101 + 6 × 100 =
+ 5 × 101
+ 6 × 100
= 3000 + 400 + 50 + 6 = 3456(10), то в шестнадцатеричной системе:
3 × 162 3 × 4096 12288
3456 = + 4 × 162 = + 4 × 256 + 1024
+ 5 × 161 + 5 × 16 + 80
+ 6 × 160 + 6 + 6
Стало быть: 3456(10) ≠ 13369(16) .
В дальнейшем нам потребуется только четыре первые степени:
16:161 = 16; 162 = 256; 163 = 4096 и 164 = 65536(10)
Так шестнадцатеричное число преобразуется в десятичное. Для того чтобы преобразовать десятичное число в шестнадцатеричное, надо сначала преобразовать его в двоичное, а затем полученное двоичное число преобразовать в шестнадцатеричное по следующим правилам:
1. делим двоичное число с правой стороны на группы по четыре бита;
2. преобразуем каждую группу в шестнадцатеричную цифру.
Для преобразования шестнадцатеричного числа в двоичное те же действия выполняются в обратном порядке.
1. Выражаем каждую шестнадцатеричную цифру в виде четырех битов
Таблица 5
Преобразование двоичных чисел в шестнадцатеричные и обратно
| Двоичные 1000101011010010 1000 1010 1101 0010 8 А D 2 Шестнадцатеричное 8АD2 Шестнадцатеричное 8АD2 8 А D 2 1000 1010 1101 0010 Двоичные 1000101011010010 | Двоичные | Шестнадцатеричные A B C D E F |
Как видно из таб. 5, преобразовать двоичное число в шестнадцатеричное или наоборот весьма просто. Посмотрим, почему так. Возьмем двоичное число 1000101011010010, для него можно написать:
1000101011010010(2) = (1×215 + 0×214 + 0×213 + 0×212) + (1×211 + 0×210 + 1×29 +
+ 0×28) + (1×27 + 1×26 + 0×25 + 1×24) + (0×23 + 0×22 + 1×21 + 0×20) =
= 212 × (1×23 + 0×22 + 0×21 + 0×20) +
+ 28 × (1×23 + 0×22 + 1×21 + 0×20) +
+ 24 × (1×23 + 1×22 + 0×21 + 1×20) +
+ 22 × (0×23 + 0×22 + 1×21 + 0×20) =
= 212 × 8 + 28 × 10 + 24 × 13 + 20 × 2 =
= (24)3 × 8 + (24)2 × 10 + (24)1 × 13 + (24)0 × 2 =
= 163 ×8 + 162 × 10 + 161 × 13 + 160 × 2 = 8АD2(16) ,
то есть шестнадцатеричное число 8АD2.
Таким образом, при преобразовании используется то обстоятельство, что 16 является целой степенью 2.
Шестнадцатеричная система очень широко используется при программировании на машинном языке. Объясняется это тем, что работать с большими двоичными числами очень неудобно. Записывая, например, двоичное число 1011011101001000 легко ошибиться из-за большого количества единиц и нулей, лучше все двоичные числа записать в шестнадцатеричной форме, если только в силу каких-то причин не требуется анализ отдельных битов. Например, изменение значения самого левого бита в шестнадцатеричном числе С8 сделает из него 48, поскольку С8 — это двоичное 11001000, и изменение значения левого бита дает 01001000, что в шестнадцатеричной форме составляет 48.
Шестнадцатеричное сложение и вычитание[5]
Не только двоичная и десятичная, но и все подобные системы счисления имеют схожие правила сложения и вычитания. Шестнадцатеричная система отличается от десятичной только тем, что 10 надо заменить на 16, в остальном правила те же. Пусть надо сложить шестнадцатеричные числа:
|
2С84
Е409
Сложение выполняется справа налево следующим образом:
1) 5 плюс 4 равно 9 (как в десятичной системе);
2) 8 плюс 8 равно 10 (чему в десятичной системе соответствует 8 + 8 = 16). Записываем 0 и переносим 1;
3) 7 плюс С равно 13 (в десятичной системе этому соответствует 7 + 12 = 19. 13 + 1 (от переноса) равно 14, записываем 4 и переносим 1;
4) В плюс 2 равно D, плюс 1 от переноса – Е (в десятичной системе 11 + 2 + 1 = =14).
Рассмотрим теперь пример с вычитанием:
|
2Е5А
54F4
На этот раз процедура такова:
1) Е минус А равно 4 (в десятичной форме 14 – 10 = 4);
2) 4 минус 5 требует занять 1, после чего 14 минус 5 равно F (не 9 – будьте внимательны!) (в десятичной форме 14 − 5 превращается в 20 − 5, то есть 15, что представляет собой шестнадцатеричное F);
3) 3 минус Е требует занять 1, получается 13 минус Е, однако 1 из этого разряда была занята, следовательно, остается 12 минус Е что равно 4 (в десятичной форме 18 – 14 = 4);
4) 8 минус 2, а с учетом занятой 1 (единицы), 7 минус 2 равно 5, как и в десятичной форме.
Выполняя сложение шестнадцатеричных чисел, не забывайте, что перенос возникает, только если сумма превышает F. Так в десятичной системе 25 + 25 = 50, но в шестнадцатеричной 25 + 25 = 4А, а не 5А (5 + 5 = А) без всякого переноса).
Некоторые шестнадцатеричные числа, например В5 или DEF7, напоминают по виду имена переменных, и следует позаботиться о том, чтобы не возникало путаницы. Например, система LISA требует записи шестнадцатеричного числа В5 в виде $ В5, чтобы отличить его от переменной с именем В5. Другие системы, например, программа-монитор Эпл, предполагают, что все величины даются в шестнадцатеричной форме и знак $ оказывается не нужным (и даже незаконным). Большинство систем программирования на Бейсике не используют шестнадцатеричных чисел, и В5 в Бейсике всегда обозначает имя переменной, а не шестнадцатеричную константу.
Двоичные и шестнадцатеричные числа можно умножать и делить. Дроби, например 1/2 также можно выразить в двоичной или шестнадцатеричной форме.
Двоичные и шестнадцатеричные дроби[5]
Вопрос: Как представить в двоичной или шестнадцатеричной системе дробные числа? Один из способов заключается в использовании принципа образования десятичных дробей.
Как мы вычисляем значение десятичной дроби .738. Оно, несомненно, равно 738/1000, но почему деление производится на 1000, а не на 100 или 10000? Потому что в числе 738 три цифры, а 103 есть 1000. Мы можем применить ту же идею к двоичным числам.
Так .101 представляет 5 (то есть .101 в двоичной системе) деленное на 8 (представляет собой 23, поскольку в числе 101 три цифры), другими словами .101 = 5/8. Число .101 называется двоичной дробью (по аналогии с десятичными дробями) (см. табл. 7). Точка .101 носит название двоичной точки (по аналогии с десятичной точкой).
Таблица 6
Двоичные и шестнадцатеричные дроби
| Двоичные | Простые | 16-ричные |
| .0 | .0 | |
| .0001 | 1/16 | .1 |
| .001 | 1/8 | .2 • А* |
| .0011 | 3/16 | .3 |
| .01 | 1/4 | .4 |
| .0101 | 5/16 | .5 |
| .011 | 3/8 | .6 |
| .0111 | 7/16 | .7 |
| .1 | 1/2 | .8 |
| .1001 | 9/16 | .9 |
| .101 | 5/8 | .А |
| .1011 | 11/16 | .В |
| .11 | 3/4 | .С |
| .1101 | 13/16 | .D |
| .111 | 7/8 | .E |
| .1111 | 15/16 | .F |
| 1.0 | 1.0 |
Нам понятно, что некоторые десятичные дроби являются конечными, а другие – нет. Так 3/4 = 0,75, потому что 3/4 = 75/100; но 1/3 представляет собой бесконечную десятичную дробь 0.3333... и т.д. (до бесконечности). То же относится к двоичным дробям, например, двоичная дробь 0.010101 и т.д. (до бесконечности) представляет собой 1/3.
Данную бесконечную десятичную дробь, например: .736736736 (и т.д. до бесконечности), можно преобразовать в простую дробь делением повторяющейся части (в данном случае 736) на 10D-1, где D – количество цифр в повторяющейся части. В данном случае мы получаем 736/999 (вспомним, что просто .736 представляет собой 736/1000).
Аналогичные правила применимы и к двоичным дробям: .01 = 1/4 (то есть 1 деленная на вторую степень двух, поскольку в .01 две цифры), а .01010101 (и т.д. до бесконечности) равно 1/3, поскольку 3 = 22 – 1.
Почему мы не можем представить 1/3 в ЭВМ в виде двух целых 1 и 3, а затем складывать, вычитать, умножать и делить дроби в соответствии с правилами, которые мы изучаем в начальной школе? Потому что нам пришлось бы постоянно сокращать получающиеся дроби, а эта операция требует очень много машинного времени. Кроме того, многие числа, с которыми нам надо работать, например, π не выражаются через простые дроби. Некоторые дроби, являющиеся конечными в десятичной системе, оказываются бесконечными в двоичной. Например, 3/16 представляет собой .0011 в двоичной системе, и согласно приведенному выше правилу 3 / (16-1) или 3/15, равно .001100110011 и т.д. (до бесконечности), но 3/15 после сокращения дает 1/5, чему в десятичной системе соответствует конечная дробь 0.2 (поскольку 1/5 = 2/10).
В дополнение к десятичным дробям вроде 0.75 в десятичной системе имеются и смешанные числа, например: 3.25, для которых характерно наличие и целой, и дробно частей. То же справедливо и по отношению и целой и дробной частям. То же справедливо и по отношению к двоичной системе, например 11.01 представляет собой двоичное представление 3.25.
Пусть теперь мы хотим представить 11.01 в виде 16-разрядной величины Мы можем договориться, что первые 10 разрядов нашей 16-разрядной величины отводится для целых чисел, за ними стоит двоичная точка, а за ней – 6 разрядов для дробной части. Тогда число 11.01 представляется в виде 0000000011.010000.
При использовании такого представления всегда возникает вопрос, где расположить двоичную точку. Если двоичная точка стоит после первых десяти разрядов, как в приведенном примере, то мы можем выразить числа от 0 (то есть 0000000000.000000) до 1023 63/64 (1111111111.111111).
Если этот диапазон слишком велик, мы можем поставить десятичную точку в другом месте, скажем, после первых 7 разрядов. Это даст нам представление чисел от 0 до (почти) 128, и увеличит количество возможных дробей с соседними числами.
Таким образом, получается, что мы можем расположить двоичную точку произвольным образом в любом месте, но, определив положение точки, мы его должны зафиксировать, чтобы выполнить сложение и вычитание. В этом случае действие в виде:
|
0011010110.100111
1001100111.011001
|
0001001101.101100
0011101101.110000
выполняется как с 16-разрядными целыми числами. Это, однако, возможно, если двоичные точки «выравнены», в противном случае нам пришлось бы сдвигать одно или другое число для выравнивания двоичных точек.
Описанное представление чисел носит название представлениесфиксированнойточкой.
В представлении с фиксированной точкой отрицательные числа записываются в виде их дополнений до двух. В этом случае диапазон чисел в нашем примере (с двоичной точкой после 10 цифр становится от -512 (то есть 1000000000.000000) до 511 63/64 (то есть 0111111111.111111)).
Существуют также шестнадцатеричные дроби, содержащие шестнадцатеричные цифры (причем .8 = 1/2; .С = 3/4 и т.д.).
Шестнадцатеричные дроби можно преобразовать в двоичные, заменив каждую шестнадцатеричную цифру 4-мя двоичными. Преобразование двоичных дробей в шестнадцатеричные также выполняется по правилам преобразования целых чисел.
Многобайтовые величины и дополнение до двух[5]
Может показаться странным, что при использовании 8-разрядных ячеек мы сталкиваемся с трудностью, поскольку в них можно хранить лишь числа от 0 до 255. Мы не можем записать в такую ячейку большое число (больше 255) или отрицательное число (менее 0). Для хранения в ЭВМ больших и отрицательных чисел используются специальные приемы
Таблица 7
Дополнение до 2-х целых чисел
| Десятичные | Двоичные | Шестнадцатеричные |
| -5 | FB | |
| -4 | FC | |
| -3 | FD | |
| -2 | FE | |
| -1 | FF | |
Для хранения больших чисел можно использовать несколько ячеек для каждого числа. Если взять 2 ячейки, то диапазон записываемых чисел увеличится до 216 – 1, или 65535. Пусть одна ячейка содержит число р, а другая – число d, тогда обе ячейки вместе содержат число 256 p+d. Если же использовать более 2 ячеек, например, n ячеек, то появится возможность хранить любые числа от 0 до 28n – l. Если, например, n = 4, то 28n – 1 = 232 – 1, что превышает 4000000000.
Отрицательные числа можно записывать двумя способами.
Первый заключается в том, что самый левый разряд отводится под код знака: 0 означает положительное число, а 1 – отрицательное. В 8-разрядной ячейке 10000011 будет представлять – 3: первая 1 означает, что число отрицательное, а остальная часть содержимого ячейки, 0000011, представляет собой 3 (с 5-лидирующими нулями). Такая запись называется знаковым представлением в прямом коде. Сейчас такой способ представления не используется.
Другой способ представления отрицательных чисел напоминает работу электрического 3-разрядного счетчика, используемого во многих магнитофонах. При обратной перемотке ленты счетчик считает назад; после 000 счетчик показывает 999, затем 998 и т.д. Точно также, если мы будем вычитать, то после 00000000 будет 11111111, затем 11111110 и т.д. В результате 11111111 можно считать представлением – 1, 11111110 – представлением – 2 и т.д.
Полученные таким образом представления чисел от -5 до +5 в десятичной, двоичной и шестнадцатеричной форме приведены в табл. 7 .
Представление -Х можно найти, вычтя Х из двоичного 100000000. Так, например, десятичному -45 соответствует двоичное 101101. Вычтя это число из 100000000, получим 11010011. Легче вычесть Х из двоичного 11111111, а затем добавить 1 к результату (это эквивалентно, поскольку 11111111+1= 100000000). Таким образом, возможны два пути:
|
|
10110100101101
|
1
Второй способ проще, так как избавляет от необходимости занимать 1 в старшем разряде. Каждая отрицательная операция вычитания представляет собой либо 1 – 0 = 1, либо 1 – 1 = 0. Фактически нам даже не нужно вычитать, просто вместо каждого 0 запишем 1, а вместо каждой 1 – 0. Такая операция называется нахождением обратного кода, или дополнения до единицы (обратный код 0 есть 1; обратный код 1 есть 0). Прибавление же к обратному коду 1 дает нам дополнение до двух.
Таким образом, использование системы представления дополнением до двух даст возможность записывать в d-разрядном регистре отрицательные числа – х, как дополнение х до двух, или 2d − x. Как и в случае знакового представления в прямом коде положительные числа начинаются с 0, отрицательные − с 1. Если d = 8, то самое большое число в рассматриваемом представлении равно 01111111 (десятичное 127), а самое маленькое –10000000 (десятичное –128). В общем случае диапазон представленных чисел заключен от 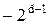 до
до 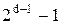 ; числа в этом диапазоне называются числами со знаком. Число 45 в системе представления дополнением до двух есть 00101101; число – 45 в системе представления дополнением до двух есть 11010011 (другими словами, это есть дополнение до двух числа 45). Дополнение до двух отрицательного числа находится точно также: к обратному коду числа прибавляется (не вычитается!) 1; так обратный код числа 11010011 есть 00101100, и после прибавления 1 получаем 00101101.
; числа в этом диапазоне называются числами со знаком. Число 45 в системе представления дополнением до двух есть 00101101; число – 45 в системе представления дополнением до двух есть 11010011 (другими словами, это есть дополнение до двух числа 45). Дополнение до двух отрицательного числа находится точно также: к обратному коду числа прибавляется (не вычитается!) 1; так обратный код числа 11010011 есть 00101100, и после прибавления 1 получаем 00101101.
Система представления чисел дополнение до двух используется практически во всех современных ЭВМ. Она удобна тем, что операции сложения чисел со знаком и без знака, выполняются одинаково (рис. 13).
| Беззнаковое представление | Двоичное
        представление представление
| Знаковое представление |
|
|
|







 3 0 0 0 0 0 0 1 1 3
3 0 0 0 0 0 0 1 1 3










 251 1 1 1 1 1 0 1 1 (-5)
251 1 1 1 1 1 0 1 1 (-5)
254 1 1 1 1 1 1 1 0 - 2
Рис. 13. Операции сложения чисел со знаком и без знака
Заметим, что если код 11111011 выражает число без знака, то он не может обозначать – 5 и должен, следовательно, рассматриваться как 251; если код
выражает число со знаком, он не может обозначать 251 (вспомним, что числа со
знаком лежат в диапазоне от – 128 до 127) и должен, следовательно, рассматриваться как –5. Мы часто используем двоичное число для обозначения
двух различных чисел (в приведенном примере 11111011 обозначает и 251, и
− 5), и, как видно из примера, никакой путаницы не возникает. Однако мы
должны помнить, какого рода данные представляют наши двоичные числа,
потому что нет никакого способа определить, что хранится в регистре или ячейке: число со знаком, число без знака или еще какое-то данное, хотя в языках высокого уровня, например в Лисп, такая проверка возможна, но используется специальный прием. Процессор 6502 может также выполнять вычисления с дробями, но этот вопрос будет рассмотрен позднее.
Действительные числа и представление с плавающей точкой [5]
Представление с фиксированной точкой, не позволяет работать с очень большими и очень маленькими числами (такими, как 6.061×1023 или 6.626×10-27), встречающимися в вычислениях. Для того чтобы на ЭВМ можно было обрабатывать действительные числа, обычно используется другое представление, называемое представлением с плавающей точкой.
В основе представления чисел с плавающей точкой лежит то, что в общем случае для определения действительного числа (например. 6.626×10-27) требуется следующая информация:
а) знак (положительный или отрицательный);
б) порядок (т.е. показатель степени десяти, в данном случае -27, хотя в формате числа с плавающей точкой в действительности используется степень двух или иногда 16, а не 10);
в) мантисса (т.е. число 6.626, выраженное в виде правильной дроби), для чего число 6.626×10-27 мы должны записать в виде .6626×10-26. Полученная мантисса .6626 представляет собой правильную дробь.
Указанной информации достаточно, чтобы выразить действительное число, поэтому все, что нам осталось сделать – это задать формат числа. Существуют различные форматы чисел с плавающей точкой; ниже описан «короткий формат», используемый на больших ЭВМ фирмы IBM например, серии 4300:
1. Каждое действительное число занимает 4 байта.
2. Левый разряд первого байта является знаковым; 0 означает плюс, а 1 – минус, как и у целых чисел.
3. Оставшаяся часть первого байта является порядком.
4. Остальные 3 байта представляют собой мантиссу.
5. Порядок представляет собой степень 16 (это необычно; в большинстве форматов чисел с плавающей точкой это степень 2).
6. Мантисса рассматривается как 6-разрядная шестнадцатеричная дробь, в пределах от .100000 до .FFFFFF (если мантисса меньше .100000, мы используем соотношение .0ххххх×16n = ххххх0×16n-1, если нужно – многократно, чтобы нормализовать мантиссу, то есть привести ее к указанному диапазону).
7. Порядок, находящийся в пределах от -64 до 63, смещают, прибавляя к нему 64; реализующая величина лежит в пределах от 0 до 127. Таким образом, порядок е в действительности представлен числом е + 64. (Это напоминает смещение напряжения в электронных цепях путем прибавления к нему постоянного положительного напряжения, так что при любых флуктуациях напряжение остается положительным.)
Если два числа с плавающей точкой нормализованы (то есть имеют нормализованные мантиссы, как это описано выше в п. 6), то в результате смещения число, у которого больше порядок, и само больше другого. Поэтому, сравнивая числа с плавающей точкой, мы можем сначала сравнивать их порядки, а затем, если порядки равны, сравнивать мантиссы. При сравнении порядков смещение преобразует знаковое сравнение с беззнаковым. Фактически и само смещение формируется также: оно содержит 1 с цепочкой нулей.
На рис. 14 показано представление чисел 2, 48, -228 и 1/512 в описанном выше формате с плавающей точкой. Обратите внимание, как значение порядка изменяет фактическое положение двоичной (или шестнадцатеричной) точки, которая «плавает» по мантиссе (в том числе «доплывая» иногда до самого левого или до самого правого края), что и дало название этому формату.
Число нуль в формате с плавающей точкой характеризуется мантиссой, равной 0; знак и порядок в этом случае не имеют значения, но принято и их делать равными 0. Заметьте, что для изменения знака числа с плавающей точкой в указанном формате достаточно изменить 1 бит (в знаковом разряде); для чисел записанных в форме дополнения до двух, это было не так (однако, существуют другие распространенные форматы чисел с плавающей точкой, для которых это замечание несправедливо).
Знак Смещение2. 0 0 0 0 0

0 1000001 0100 0000 0000 0000 0000 0000
Порядок Мантисса f = .200000
е = 1 (смещенное) (шестнадцатеричное)
Число = 16е × f = 161 × .2 = 2
Знак Смещение 3 0. 0 0 0 0

0 1000010 0011 0000 0000 0000 0000 0000
Порядок Мантисса f = .300000
е = 2 (смещенное) (шестнадцатеричное)
Число = 16е × f = 162 × .3 = 30 (шестнадцатеричное) = 48 (десятичное)
Знак Смещение−1 0 0 0 0 0 0 0

0 1001000 0001 0000 0000 0000 0000 0000
Порядок Мантисса f = .100000
е = 8 (смещенное) (шестнадцатеричное)
Число = -16е × f = -168 × .1 = -10000000 (шестнадцатеричное)
.0 0 8 0 0 0 0 0
Знак Смещение

0 0111110 1000 0000 0000 0000 0000 0000
Порядок Мантисса f = .800000
е = -2 (смещенное) (шестнадцатеричное)
Число = 16е × f = 16-2 × .8 = .008 (шестнадцатеричное) = 1/512 (десятичное)
Рис. 14. Представление действительных чисел в формате с плавающей точкой
Операции с плавающей точкой[5]
Пусть мы подучили несколько чисел, представленных в формате с плавающей точкой. Что нам с ними делать? Работая с процессором 6502, мы вызываем подпрограммы, чтобы складывать, вычитать, умножать или делить эти числа, преобразовывать их в целые и наоборот, вводить и выводить. Умножение и деление чисел с плавающей точкой в действительности проще сложения и вычитания. Число с плавающей точкой, характеризуемое знаком s, порядком е и мантиссой f, может быть представлена в виде s×be×f, где b – база (b = 16), a s – знак, который принимается равным 1 для положительных чисел и -1 для отрицательных. Произведение 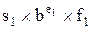 на
на 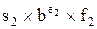 равно
равно 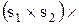
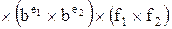 , причем
, причем 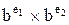 можно выразить как
можно выразить как 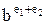 . Отсюда, для умножения двух чисел с плавающей точкой достаточно перемножить знаки, сложить порядки и перемножить мантиссы. Результат может оказаться не нормализованным – например, мантисса .3, умноженная на самое себя, дает .09. Однако если результат не нормализован, процедуру нормализации следует принимать только один раз.
. Отсюда, для умножения двух чисел с плавающей точкой достаточно перемножить знаки, сложить порядки и перемножить мантиссы. Результат может оказаться не нормализованным – например, мантисса .3, умноженная на самое себя, дает .09. Однако если результат не нормализован, процедуру нормализации следует принимать только один раз.
Аналогично деление 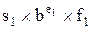 на
на 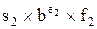 равно
равно 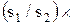
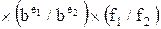 , причем
, причем 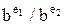 можно выразить как
можно выразить как 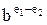 . Таким образом, в данном случае мы должны разделить знаки, найти разность порядков и разделить мантиссы.
. Таким образом, в данном случае мы должны разделить знаки, найти разность порядков и разделить мантиссы.
Как и в случае умножения, результат может оказаться не нормализованным – мантисса .F, разделенная на .1, дает в шестнадцатеричной системе F, но, как и раньше, процедуру нормализации следует применить только 1 раз (в противоположном, по отношению к операции умножения, направлении). Относительная сложность сложения и вычитания связана с необходимостью сдвигов, если двоичные точки в числах не выровнены. Например:
|
|
|
2.359 2.359
238.259
И вообще, при сложении двух десятичных дробей мы должны сдвигать одну из них до тех пор, пока не выровняются их десятичные точки. Из рис. 14 видно, что двоичная точка в числе с плавающей точкой «переплывает» на одну позицию вправо каждый раз, когда порядок увеличивается на 1. Поэтому, если разность между порядками составляет z, перед сложением меньшее число надо сдвинуть на z позиций вправо – в данном случае на z шестнадцатеричных разрядов, или 4z двоичных. То же справедливо в случае операции вычитания.
Знаки чисел с плавающей точкой, участвующих в операциях сложения или вычитания, определяют действительный тип выполняемой операции. Если знаки неравны, тогда то, что было определено как сложение, становится вычитанием и наоборот.
Вычитание – это единственная операция с плавающей точкой, когда может потребоваться многократное применение процедуры нормализации. Например, шестнадцатеричное вычитание
|
.532271
.000413
дает дробь с тремя лидирующими нулями, так что процедуру нормализации следует применить три раза
Не надо забывать, что числа с плавающей точкой лишь приблизительно описывают действительные числа, и последовательность операций с плавающей точкой может легко уменьшить точность. Это в особенности касается вычитания, хотя на первый взгляд вычитание может показаться точной операцией (см. пример выше). Если первая мантисса в этом примере изменится на единицу младшего разряда, результат становится равным .000412, или .412000×163, то есть изменится на 1000 (шестнадцатеричное), а совсем не на 1. Сложение, умножение и деление чисел с плавающей точкой могут давать ошибочные результаты, даже если сами складываемые, умножаемые или делимые числа вполне точны.
Регистры, ячейки и байты [5]
Представим себе, что ЭВМ содержит большое количество коробочек для хранения чисел. В каждую коробочку помещается 8 бит, поэтому она может содержать любое число от 00000000 до 11111111 (при этом любое число в любой момент времени). Существует два вида коробочек. Одни называются регистрами, рассмотрим только А, Х, У. Другие называются ячейки, и все ячейки вместе взятые, образуют основную или оперативную память. Максимальное количество ячеек (правда, без привлечения специальных технических средств) составляет 65536 или 216. Каждый регистр или ячейка может содержать любое 2-х разрядное шестнадцатеричное число от 00 до FF.FF(16) = 255(10), поэтому каждый регистр или ячейка может содержать любое десятичное число, не превышающее 255. Заметим, что 255 = 256 – 1 = 28 − 1. Число 28 представляет в двоичной системе 100000000, то есть 1(ед.), за которой следует восемь нулей, поскольку вычесть 1 (ед.) = 11111111. Таков принцип двоичной системы: если имеется n бит (у нас n = 8), то можно записать любое число от 0 до 2n – 1 (у нас до 28 – 1).
Ячейки оперативной (основной) памяти имеют номера, называемые адресами, отсчет которых начинается с нуля. Например, ячейка 0, и т.д.; к этим
ячейкам можно обратиться по адресу 0, 1 и т.д. Максимально возможный
адрес = 65535 или 216 – 1 , поскольку максимальное число ячеек взятых с адресом 0 составляет 65536. Таким образом, любой адрес в пределах от 0 до 216 – 1 можно записать с помощью 16 бит или в двух ячейках (рис. 16).




 | |||
 | |||

 | |||||
 |  | ||||
Рис. 15. Выбор ячеки 5 (1 Ø 12); запись в ОЗУ
Рис. 16. 2-х байтовая ячейка
7 0 7 0
Регистр А Регистр Х
Рис. 17.
Пример: число 1600(10) = 11001000000. Теперь разместим их в двух ячейках (регистр А и X) (рис. 17). В регистре А число 6(10) , в регистра Х – 64(10). Bместе регистры содержат 1600, занимающее 16 двоичных разряда Для получения этого числа надо вычислить значение выражения: 256 × А + Х:
256 × 6 + 64 = 1536 + 64 = 1600
Помимо адресов, или номеров, отдельные ячейки в программе имеют имена. Если у вас есть ячейка с именем К, мы можем хранить в ней значение К
BASIC: FOR K = 1 TO 100
(следующие предложения)
NEXT K
Переменная К принимает значения от 1 до 100. Все эти значения можно хранить в ячейке с именем К, например, если К = 55, то в ячейке содержится число 55. Могут встречаться 8, 24, 36 разряда и т.д. 8 бит введено видимо фирмой IBM. 8 бит = 1 Байт. Для хранения байта требуется 2 ячейки оперативной памяти. Если говорим 65536 Байт памяти, 64 К, то есть, умножены на 1Кб (1024 байт). Кроме ОП ЭВМ содержит вспомогательную память. Магнитная дискета (105 Байт памяти), ее необходимо переписать в оперативную память.
Нельзя: путать адрес ячейки с содержащимся в ней числом. Например, ячейка с адресом 6 может содержать любое число от 0 до 255, и совсем не обязательно число 6. 6 – это просто шестая ячейка ЭВМ и ничего более.
На рис. 15 происходит выбор ячейки 5(101) с записью в ОЗУ.
Инкремент и декремент [5]
Любая ЭВМ предоставляет возможность сложения и вычитания. В программах для процессора 6502 при сложении и вычитании используются специальные приемы, но мы познакомимся с двумя простыми операциями: прибавление 1 (эта операция известна под названием инкремент) и вычитание 1 (так называемый декремент).
В процессоре 6502 предусмотрены 6 команд инкремента и декремента.
INC v Инкремент v
DEC v Декремент v
INX Инкремент регистра X
DEX Декремент регистра X
INY Инкремент регистра Y
DEY Декремент регистра Y
Здесь, как и раньше, v обозначает любую ячейку оперативной памяти. Заметим, что мы не можем выполнить инкремент или декремент регистра А.
Выполним с помощью указанных команд предложение Бейсика K = L + 1. Для этого понадобятся 3 шага:
1. Загрузка L в регистр.
2. Инкремент регистра (+1 к его содержимому).
3. Запись содержимого регистра в К
При использовании регистра X потребуется такая последовательность команд:
LDX L
INX
STX К
Точно так же можно выполнить операцию U = V – 1, используя, например, регистр Y:
LDY V
DEY
STY U
Если же надо выполнить операцию К = К + 1 (то есть прибавить 1 к К), мы можем ограничиться только одной командой:
INC К
Заметим, что последовательность команд
INC L
LDA L
STA К
также выполняет операцию K = L + 1. Однако такое решение не является наилучшим, так как одновременно с К изменяется L, хотя, записывая K = L + 1, мы предполагаем, что изменится только К.
Команды инкремента и декремента часто используются для прибавления или вычитания 2. Для того, чтобы выполнить операцию К = L + 2, надо написать
LDX L
INХ
INX
STX К
Выполнить К = К – 2 можно проще:
DEC К
DEC К
Таким образом, можно прибавлять или вычитать 3, 4 и т.д., но обычно для этого используются команды сложения и вычитания. Важно помнить, что команды INC К и DEC К не изменяют содержимое регистра А. Так последовательность команд INC К и STA L не сделают L равным К + 1.
Инкремент 255 дает 0, а декремент 0 дает 255. Действительно, если регистр X содержит 0 (двоичное число 00000000), то в результате выполнения команды DEX в регистре X теперь будет 11111111 (что представляет собой число без знака 255 или число со знаком -1).
Точно так же, если регистр Y содержит двоичное число 11111111, то в результате выполнения команды INY в регистре будет 0.
Стеки [5]
Или, проще говоря – стековая память. Фирмы-изготовители микропроцессоров в описании технических характеристик указывают, что «... микропроцессор работает со стековой памятью». Например, нам необходимо решить уравнение а2 + b2 = с2. Мы можем представить, что – а × а = a2, b × b = b2 и соответственно − с × с = с2. Запишем в виде подпрограммы, при решении сложной задачи, нам необходимо многократно обращаться к данной подпрограмме, ее расписывать, что крайне неудобно. Для упрощения решения задачи мы составим данную программу в виде подпрограммы и запишем ее на жесткий диск. При многократном использовании данного выражения, МП вызывает данную подпрограмму с жесткого диска, подставляет в решение задачи, а после выполнения – снова выгружает на жесткий диск. Экономится оперативная память и работать очень удобно. Рассмотрим рис. 18.
Р1 Р2
 -
-
- -
-
-
 call P2
- call P2
-
  α -
-
call P2
- α -
-
call P2
-
 β -
-
call P2
- β -
-
call P2
-
 Y -
- Y -
-
| RETURN |
Рис. 18. Многократный вызов подпрограммы
На нем изображена программа Р1, которая трижды из разных точек обращается к подпрограмме Р2 (программа Р1 может быть основной программой, а может быть и подпрограммой, мы называем ее вызывающей программой, то есть программой, которая вызывает подпрограмму Р2).
Предложение вызова или перехода на подпрограмму (JSR P2, где JSR-(англ.) – переход на подпрограмму), очевидно, выполняет переход на Р2.
Предложение возврата RTS (RTS − возврат из подпрограммы), очевидно, выполняет на переход. Но куда? При первом обращении к Р2 предложение возврата вызовет переход в точку α. Во второй раз будет переход в точку β, в третий раз в точку Y.
Так же одна и та же команда может вызвать переход в три разные точки. Ответ заключается в механизме работы команды перехода на подпрограмму. Эта команда не только выполняет переход, но также вычисляет и сохраняет в памяти адрес возврата, который представляет собой адрес команды, следующей за JSR. При первом вызове Р2 адресом возврата является α; при втором вызове – β; при третьем –Y.
Команда возврата теперь может выполнить переход по адресу возврата, поскольку он хранится в памяти. Поэтому первый раз команда RTS вызовет переход на α, второй раз – на β; третий раз – на Y, как и требуется.
Следующий вопрос заключается в том, где хранить адрес возврата. В действительности команда JSR записывает адрес возврата в некоторую структуру данных, называемую стеком; команда RTS извлекает адрес возврата из стека и производит переход. Такой способ хранения адресов возврата является прогрессивной особенностью процессора 6502 (как и ряда других микропроцессоров) и приводит, как мы увидим, к значительной экономии времени и памяти. Чтобы понять, почему это так, мы должны рассмотреть, что представляют собой стеки. Стек представляет собой массив переменной длины. Назовем этот стек Н, а его размер (длину) – X. Тогда можно считать, что массив Н состоит из элементов от Н(0) до Н(Х-1).
Размер стека увеличивается, если Н(х) присвоить значение некоторой величины А, а затем к Н прибавить единицу. Такая операция называется проталкиванием А в стек (см. рис. 19).
| Н (новое Х−1) | ||||||
| А (Х−1) | Н (Х−1) | Н (новое Х−2) | ||||
| - - - |
- - | -
 -
- -
-
| ||||
| Н (0) | Н (0) | Н (0) |
Рис. 19. Проталкивание
| А (Х−1) | Н (новое Х) | |||||
-
- - | Н (новое Х −1) | Н (новое Х −1) | ||||
-
 -
- -
-
| - - - | |||||
| Н (0) | Н (0) | Н (0) |
Рис. 20. Выталкивание
Мы можем уменьшить размер стека, вычитая 1 из X. При этом Н (X) снова попадет в А. Это обычно называется выталкиванием из стека.
И проталкивание, и выталкивание можно выполнить на Бейсике (рис. 19, 20):
Н(Х) = А Х = Х – 1
Х = Х + 1 А = Н(Х)
Проталкивание А Выталкивание А
Или на языке Ассемблера процессора 6502 с помощью регистров А и X
STA H, X DEX
INA LDA H.X
Проталкивание А Выталкивание А
Любой стек имеет максимальный размер, который мы будем обозначать
max, так что всегда Х < mах. Для процессора 6502 обычно max = 256, так что
максимальным допустимым значением (без знака) содержимого регистра Х при
любых условиях являются Х < 256 или Х ≤ 255 (где 28-1 = 255-1, для 8-разрядной ЭВМ).
Теперь представим себе, что мы только протолкнули величины Р3, Р2 и Р1 (именно в этом порядке) в стек. Мы говорим, что Р1 находится на верхушке стека; Р2 представляет второй элемент стека (считая сверху вниз); Р3 – третий элемент сверху.
И если Р3, Р2 и Р1 загружены в такой стек, то
LDA Н - !1, Х загружает Р1 (верхушку стека);
LDA Н - !2, X загружает Р2 (второй элемент сверху);
LDA Н - !3, X загружает Р3 (третий элемент сверху),
и вообще LDA Н - !n, X загружает n-й элемент сверху.
Наличие в приведенных командах знака минус наводит на мысль о перевернутом стеке. В перевернутом стеке Н байты имеют обозначение на Н(0), Н(1), Н(2) и т.д., а Н(max – 1), Н(max – 2), Н(max – 3) и т.д. вниз до Н(Х + 1), причем Н(Х) по-прежнему представляет собой элемент над верхушкой стека. Теперь Х не характеризует размер стека. Размер стека равен Z, причем max – Z = X + 1 (или Z = max – (X + 1) = max – 1 – X). Если max = 256, то Z = 255 – Х; другими словами, текущий размер стека представляет собой дополнение до единицы содержимого регистра Х.
Проталкивание и выталкивание в таком стеке производится следующим образом:
STA H, X IN X
DEX LDA H.X
Проталкивание А Выталкивание А
и если Р3, Р2 и Р1 загружены в такой стек, то
LDA Н + !1, Х загружает Р1 (верхушку стека);
LDA Н + !2, X загружает Р2 (второй элемент сверху);
LDA Н + !3, X загружает Р3 (третий элемент сверху),
и вообще LDA Н + !n, X загружает n-й элемент сверху, и мы заменили знаки минус на знаки плюс.
Дата добавления: 2016-01-30; просмотров: 1798;
