ДВОИЧНО-ДЕСЯТИЧНАЯ СИСТЕМА СЧИСЛЕНИЯ
(Методическая разработка)
Задание: Преобразовать числа, выраженные в десятичной форме, в двоичную форму, затем произвести умножение.
Примечание: Правила умножения точно такие же, как и в десятичной системе счисления.
Умножить: 5 × 5 = 25
Преобразуем десятичное число 5 в двоичный код
5 : 2 = 2 остаток 1 Полученный результат
2 : 2 = 1 остаток 0 записываем в обратном
1 : 2 = 0 остаток 1 порядке
1 0 1
Таким образом: 5 (10) = 101 (2)
Преобразуем десятичное число 25 в двоичный код
25 : 2 = 12 остаток 1
12 : 2 = 6 остаток 0 Полученный результат
6 : 2 = 3 остаток 0 записываем в обратном
3 : 2 = 1 остаток 1 порядке
1 : 2 = 0 остаток 1
1 1 0 0 1
Таким образом: 11001(2) = 25 (10)
Производим проверку:
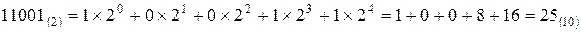
Производим двоичное умножение
|
101
|
11001
Правила умножения в двоичной системе точно такие же, как и в десятичной системе счисления.
1) 1 × 1, будет 1, записываем 1.
2) 1 × 0, будет 0, записываем 0.
3) 1 × 1, будет 1, записываем 1.
4) Записываем три нуля, причем первый ноль под вторым знаком (нулем).
5) Умножение 1 × 101 точно такое же, как и п.п. 1, 2, 3.
Производим операцию сложения.
6) Сносим и записываем 1.
7) 0 +0 будет ноль, записываем 0.
8) 1 + 1 будет 10, записываем ноль, а единицу переносим в старший разряд.
9) 0 + 0 + 1 будет 1, записываем 1
10) Сносим и записываем 1.
Задание 1: Выполнить умножение в двоичной форме
1) 8 × 10 =
2) 16 × 8 =
3) 24 × 6 =
Задание 2: Полученный результат восстановить в десятичной форме.
Задание: Преобразовать числа, выражение в десятичной форме, в двоичную форму, затем произвести деление.
Примечание: Правила деления точно такие – же, как и в десятичной системе счисления.
Если результат делится без остатка, записываем – 0, иначе (с остатком) – 1
Разделить: 10:2 = 5
Преобразуем десятичное число 10 в двоичный код:
 10:2 = 5 остаток 0
 5:2 = 2 остаток 1
 2:2 = 1 остаток 0
 1:2 = 0 остаток 1
|
Полученный результат
записываем в обратном
порядке
1 0 1 0
Таким образом: 1010(2) = 10(10)
Преобразуем десятичное 2 в двоичный код
2:2 = 1 остаток 0
1:2 = 0 остаток 1
1 0
Таким образом: 10(2) = 2(10)
Преобразуем десятичное 5 в двоичное код
5:2 = 2 остаток 1
2:2 = 1 остаток 0
1:2 = 0 остаток 1
1 0 1
Таким образом: 101(2) = 5(10)
Производим проверку:
1010(2) = 0×20 + 1×21 + 0×22 + 1×23 = 0 +2+0+8 =10(10)
10(2) = 0×20 +1×21 = 0 +2 = 2(10)
101(2) = 1×20 +0×21 +1×22 = 1+ 0+4 = 5(10)
Производим двоичное деление:
1010(2) : 10(2) = 101(2)
|
1010(2) 10
10 101
|
10
Правила деления в двоичной системе точно такие же, как и в десятичной.
1) 10 разделить на 10. Берём по 1, в результат записываем 1.
2) Сносим 1 (единицу), не хватает, занимаем 0 (ноль).
3) Берём по 1. Из 10 (десяти) вычесть 10 получается ноль, что и соответствует
действительности.
Задание 1: Выполнить деление в двоичной форме
1) 10010(2) : 110(2) =
10010 110
11000(2) : 110(2) =
11000 110
2) 110110(2) : 110(2) =
110110 110
Задание 2: Полученный результат восстановить в десятичной форме.
Задание: Вычесть числа, выраженные в двоичной форме, полученный результат восстановить в десятичную форму.
Вычесть: 1100(2) – 110(2) =
Правила вычитания в двоичной форме.
0 – 0 = 0
1 – 0 = 1
1 – 1 = 1
10 – 1 = 1
Вычитание в двоичной форме подобно вычитанию в десятичной системе.
|
110
Выполняем справа налево:
1) 0 минус 0 равно 0;
2) 10 минус 1 равно 1 (т.е. 2 минус 1 равно 1). Занимаем 1.
3) 10 (не 11, поскольку мы заполняли 1) минус 1 равно 1.
Восстанавливаем полученный результат в двоичной форме.
Правила сложения в двоичной форме:
|
110 0 + 1 = 1
1100 1 + 0 = 1
1 + 1 = 10
1) 0 плюс 0 равно 0 (См. правила сложения чисел).
2) 1 плюс 1 равно 10. Записываем ноль, а единицу переносим в старший разряд, как и в десятичной системе
3) 1 плюс 1 плюс 1 равно 11 – двоичное число. Записываем 1, а вторую единицу
переносим в старший разряд. Получаем: 1100(2), что и соответствует действительности.
Задание: Произвести проверку полученного результата .
1100(2) = 0×20 + 0×21 +1×22 +1×23 = 0 + 0 + 4 + 8 = 12(10)
110(2) = 0×20 +1×21 +1×22 = 0 + 2 + 4 = 6(10)
110(2) = 0×20 +1×21 +1×22 = 0 + 2 + 4 = 6(10)
Таким образом, получаем: 6 + 6 = 12, что соответствует действительности.
Выполнить самостоятельно:
Задание 1. Выполнить вычитание в двоичной форме:
|
|
|
111 1011 100100
Задание 2. Полученный результат выполнить в десятичной системе счисления, результаты сравнить.
Задание: Сложить числа, выраженные в двоичной форме, полученный результат восстановить в десятичную форму.
Сложить: 1010(2) + 110(2) =
Правила сложения в двоичной форме.
0 + 0 = 0
0 + 1 = 1
1 + 0 = 1
1 + 1 = 10
Сложение в двоичной форме подобно сложению в десятичной системе.
|
|
110 6(10)
10000 соответствует: 16(10)
Выполнение действий происходит следующим образом.
1) 0 плюс 0 равно О
2) 1 плюс 1 равно 10 (что 2 (два) в двоичной системе представляется как 10);
Исторически сложилось, что для сложения чисел использовалось десять пальцев и наоборот:
9 + 1 = 10; 8 + 2 = 10; 1 + 9 = 10; 2 + 8 = 10.
Поэтому и произошла десятичная система счисления. А в двоичной 2 (два) знака: 1 и 0
3) 1 плюс 0 плюс 1 равно 10. Записываем 0 и переносим 1.
4) 1 плюс 1 равно 10, поскольку это последнее действие, записываем 10, точно также сделали это в десятичной системе.
Задание: Произвести проверку полученного результата:
|
|
1106
1010 10
1. Преобразуем двоичные числа в десятичные:
1010(2) = 0×20 + 1×21 + 0×22 +1×23 = 0 + 2 + 0 + 8 = 10(10)
110(2) = 0×20 + 1×21 + 1×22 = 0 + 2 + 4 = 6(10)
10000(2) = 0×20 + 0×21 + 0×22 + 0×23 + 1×24 = 0 + 0 + 0 + 0 +16 = 16(10)
Таким образом, получаем: 10 + 6 = 16, что и соответствует действительности.
Выполнить самостоятельно:
Задание 1: Выполнить сложение следующих двоичных чисел:
|
|
|
1010110111010
Задание 2: Сложите указанные двоичные числа, затем преобразуйте каждое число в десятичную форму и убедитесь, что сумма двоичных чисел, преобразованная в двоичную форму, совпадает с полученной ранее двоичной суммой:
|
11001
Дата добавления: 2016-01-30; просмотров: 1190;