Бесконечные множества
Бесконечность обычно понимается как нечто, не имеющее границы, то есть как альтернатива конечному. В математике основной интерес к бесконечности проявляется в связи с вопросом о природе бесконечных множеств как математических объектов, то есть объектов, которые можно сравнивать количественно. Но как можно сравнивать два множества, состоящие из бесконечного числа элементов каждое? При выполнении каких условий они становятся математическими объектами?
В математике установилось два понятия бесконечности – потенциальная и актуальная.
Потенциальная бесконечность обосновывает построение и существование последовательности, рядов неограниченных геометрических форм (прямая, плоскость, пространство). В сущности, потенциальная бесконечность обосновывает принцип индукции (то есть переход от натурального числа n к числу n+1) как аксиому. Ее основной недостаток в том, что она не в состоянии определить количественные отношения между «бесконечными» объектами.
Актуальная бесконечность рассматривает «бесконечные» объекты, как завершенные, отвлекаясь от построения и свойств элементов объекта. Например, в аксиоматическом построении множества натуральных чисел потенциальная бесконечность объявляет потенциально существующим любое сколь угодно большое натуральное число, то есть имеем натуральный ряд 1, 2, …, n, …. Объявляя натуральный ряд существующим, актуальная бесконечность создает математический объект – множество натуральных чисел 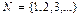 .
.
Рассматривая направленную геометрическую прямую как множество вещественных чисел, потенциальная бесконечность объявляет любую ее точку как потенциально существующее число, а добавление к прямой чисел «–¥» и «+¥» со своими правилами действий актуальная бесконечность позволяет считать такую прямую замкнутой и рассматривать ее как существующий математический объект.
Потенциальная и актуальная бесконечность взаимосвязаны и дополняют друг друга, однако до сих пор проблема единства бесконечности в математике окончательно не решена.
Натуральный ряд
Так называют бесконечное множество 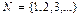 натуральных чисел, снабженных естественным порядком, то есть, помимо количественной характеристики предмета, они характеризуют и порядок расположенных элементов в ряд. Отсюда и название – натуральный ряд.
натуральных чисел, снабженных естественным порядком, то есть, помимо количественной характеристики предмета, они характеризуют и порядок расположенных элементов в ряд. Отсюда и название – натуральный ряд.
Множество N, первое из бесконечных, имеет кардинальное число 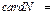 æ0 (читается алеф-ноль). Обоснование натурального ряда как множества натуральных чисел с характеристическим свойством, представленном в виде аксиом, принадлежит Дж. Пеано (1889) [11].
æ0 (читается алеф-ноль). Обоснование натурального ряда как множества натуральных чисел с характеристическим свойством, представленном в виде аксиом, принадлежит Дж. Пеано (1889) [11].
Аксиома 1. 1 (единица) есть натуральное число, то есть 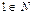 .
.
Аксиома 2. Если 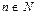 , то
, то 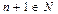 , то есть у любого натурального числа есть последующее.
, то есть у любого натурального числа есть последующее.
Аксиома 3. Если 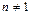 , то
, то 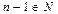 , то есть единице не предшествует никакое число.
, то есть единице не предшествует никакое число.
Аксиома 4. Если 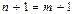 , то
, то 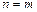 , то есть каждое число либо не является последующим ни для какого числа, либо является последующим точно для одного числа.
, то есть каждое число либо не является последующим ни для какого числа, либо является последующим точно для одного числа.
Аксиома 5 (принцип индукции). Каждое множество натуральных чисел, которое содержит число 1 и, вместе с каждым содержащимся в нем числе n содержит последующее число 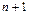 , содержит все натуральные числа.
, содержит все натуральные числа.
Метод индукции. Чтобы доказать, что некоторым свойством P обладают все числа, доказывают сначала, что им обладает число 1, а затем в предположении, что свойством P обладает некоторое число n, доказывают, что этим свойством обладает число n+1. В силу аксиомы 5 множество чисел, обладающее свойством P, должно содержать множество N.
Пример I.3. Пусть 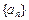 ,
, 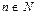 , последовательность, где
, последовательность, где 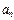 – общий член последовательности. Пусть
– общий член последовательности. Пусть 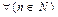 ,
, 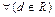 Þ
Þ
( 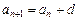 ). Такая последовательность называется арифметической прогрессией. Доказать, что общий член
). Такая последовательность называется арифметической прогрессией. Доказать, что общий член 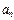 вычисляется по формуле
вычисляется по формуле
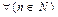 Þ (
Þ ( 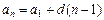 ). (I.1)
). (I.1)
Доказательство. Применим метод индукции. При 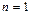 , по определению прогрессии,
, по определению прогрессии, 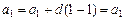 . Пусть при
. Пусть при 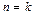 ,
, 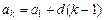 . Докажем справедливость (1) для
. Докажем справедливость (1) для 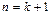 . Имеем, по определению,
. Имеем, по определению, 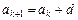 , тогда
, тогда 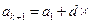
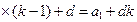 , что доказывает справедливость формулы (I.1) для любого
, что доказывает справедливость формулы (I.1) для любого 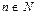 ▼.
▼.
Множество натуральных чисел замкнуто относительно операций сложения и умножения, то есть 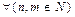 Þ
Þ 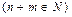 &
& 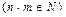 , называемые суммой и произведением, соответственно.
, называемые суммой и произведением, соответственно.
Неравенства: 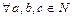 имеет место одно и только одно из соотношений
имеет место одно и только одно из соотношений
1) 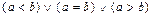 ;
;
2) если 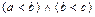 , то
, то 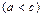 ;
;
3) если 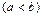 , то
, то 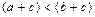 ;
;
4) если 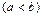 , то
, то 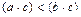 .
.
Дата добавления: 2016-01-26; просмотров: 2494;
