Вопрос 2. Метод минимального расстояния до множества

В этом методе учитывается минимальное расстояние до образцов, входящих в обу­чающую последовательность.

На рис.6 показаны расстояния 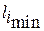и .

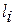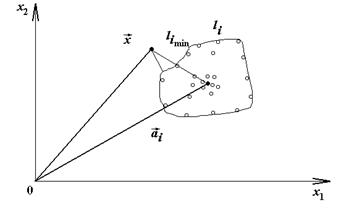
Рис.6. Метод минимального расстояния до множества

Решающее правило имеет вид

, ,

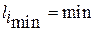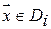т. е. если точка 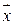ближе всего к одной из точек обучающей последовательности диагноза 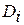, то точка относится к этому диагнозу.

Метод минимального расстояния до множества представляет собой диагностику «по прецеденту», т. е. по образцу (изделию), наиболее близко напоминающему объект, предъявленный для распознавания.

Дополнение к решающему правилу в метрических методах

Метрические методы распознавания, в отличие от вероятностных, основаны на детерминистском подходе. Решающее правило устанавливает диагноз, считая его достоверным.

Обучающая последовательность, как уже указывалось ранее, составляется из образцов (изделий), для которых достоверно известен диагноз.

По смыслу задачи распознавания, если минимальное расстояние до эталона диагноза 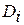мало отличается от других расстоянии, достоверность диагноза 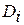вызывает сомнения.

Вводятся условные «вероятности» диагнозов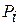

,

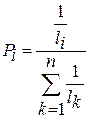где 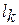– расстояние до эталона диагноза .

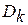Решение в пользу диагноза 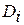принимается в случае, если

,

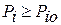где 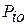– уровень принятия решения для i-го диагноза (обычно ).

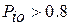Такой способ сближает вероятностные и детерминистские методы распознавания. Применение метрических методов возможно и в том случае, когда области диагнозов пересекаются.

ЛИТЕРАТУРА

1. И.А.Биргер. Техническая диагностика. – М.: Машиностроение, 1978.

2. В.А. Пивоваров. Повреждаемость и диагностирование авиационных конструкций. – М.: Транспорт, 1994

******************************************************************