Вопрос 2. Методы минимального риска

Методы минимального риска были развиты в связи с задачами радио­локации, но могут вполне успешно использоваться в задачах технической диагностики.

Пусть проводится измерение параметра 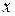(например, уровня вибраций изделия) и на основании данных измерений требуется сделать вывод о возможности продол­жения эксплуатации (диагноз 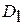– исправное состояние) или о направлении изде­лия в ремонт (диагноз 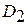– неисправное состояние).

На рис. 4 даны значения плотности вероятности диагностического параметра 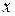для двух состояний.

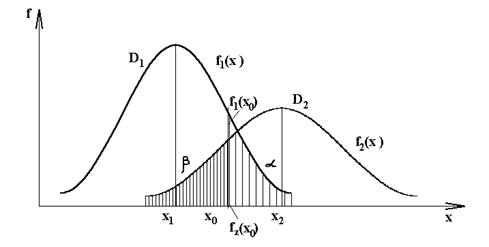
Рис. 4. Плотность вероятности диагностического признака

Пусть установлена контрольная норма для уровня вибрации 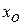. В соответствии с этой нормой принимают:

.

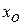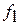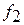Из рис. 4 следует, что любой выбор величины связан с определенным риском, так как кривые и пересекаются. Существуют два вида риска: риск «ложной тревоги», когда исправное изделие признают неисправным, и риск «пропуска цели», когда неисправное изделие считают годным.

В теории статистического контроля их называют риском поставщика и риском приемщика или ошибками первого и второго рода.

При 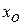вероятность ложной тревоги

,

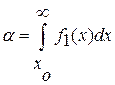вероятность пропуска цели

.

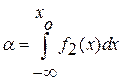Задача теории статистических решений состоит в выборе оптимального значения .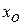

По способу минимального риска рассматривается общая стоимость риска

,

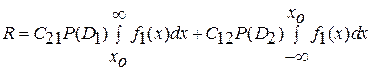где 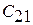– «цена» ложной тревоги; 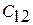– «цена» пропуска цел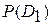и; и 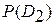– априорные вероятности диагнозов (состояний), определяемые по предварительным статистическим данным. Величина R представляет собой «среднее значение» потери при ошибочном решении.

Из необходимого условия минимума

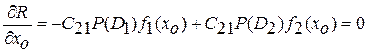
получаем

.

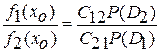Можно показать, что для одномодальных распределений данное условие всегда обеспечивает минимум величины R. Если стоимость ошибочных решений одинакова, то

.

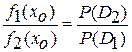Последнее соотношение минимизирует общее число ошибочных решений. Оно вытекает также из метода Байеса.

ЛИТЕРАТУРА

1. И.А.Биргер. Техническая диагностика. – М.: Машиностроение, 1978.

2. В.А. Пивоваров. Повреждаемость и диагностирование авиационных конструкций. – М.: Транспорт, 1994.

******************************************************************