Вопрос 1. Метод разделения в пространстве признаков

Одними из наиболее важных методов диагностики являются методы разделения в пространстве признаков. Эти методы основаны на естественной «гипотезе компактности», в соответствии с которой точки, отображающие одно и то же состояние (диагноз), группируются в одной области пространства признаков.

Как и в метрических методах распознавания, состояние изделия характеризуется точкой в пространстве признаков. Предполагается, что области диагнозов не пересекаются и поэтому возможно построить разделяющую поверхность.

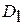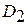Рассмотрим распознавание двух состоянии: и (дифференциальная диагностика или дихотомия).

При наличии нескольких диагнозов распознавание может быть сведено к последовательному применению рассматриваемой процедуры.

В основе методов разделения лежит построение скалярной функции параметров (признаков)

,

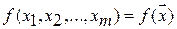принимающей различные знаки в двух областях диагноза. Такую функцию называют разделяющей, и тогда

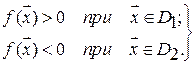
Таким образом, разделяющая функция с положительным значением для всех изделий, имеющих состояние 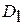, и отрицательное значение в противоположном случае.

Условие образует решающее правило для разделения в пространстве при­знаков.

Если для предъявленного для распознавания объекта, характеризующегося вектором 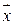, значение 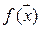положительно, объект считают принадлежащим состоянию 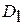, при отрицательном значении 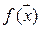– состоянию .

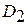Уравнение

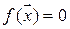
будет составлять уравнение разделяющей поверхности (поверхности, разделяющей области диагнозов).

Наиболее простой вид имеет линейная разделяющая функция

,

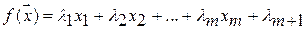где 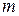– число признаков (размерность пространства);

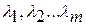– «весовые» коэффициенты.

Разделяющая поверхность будет гиперплоскостью («плоскостью» в многомерном пространстве)

.

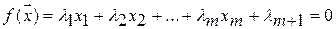Для случая двух признаков (параметров) разделяющая плоскость будет разделяющей прямой (рис.7).

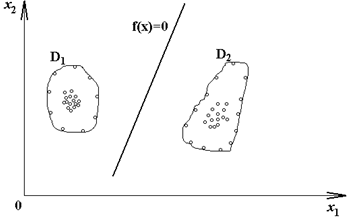
Рис.7. Линия, разделяющая функции для двух диагнозов

Для удобства геометрической интерпретации введем формально еще один параметр

.

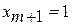Разделяющаяфункция может быть теперь представлена в виде скалярного произведения

,

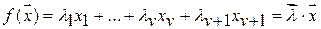где 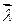– «весовой» вектор

.

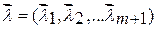Решающее правило будет таким:

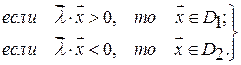
Уравнение разделяющей гиперплоскости

.

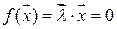Из последнего равенства следует, что разделяющая гиперповерхность перпендикулярна «весовому» вектору и проходит через начало координат (в дополненном пространстве признаков размерности ).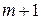

Чтобы осуществить диагностику с помощью линейной разделяющей функции, достаточно знать компоненты весового вектора.

Примем, что разделяющая плоскость проходит через точку, находящуюся на середине прямой, соединяющей точки эталонов (точку А, рис. 8), перпендикулярную этой прямой.

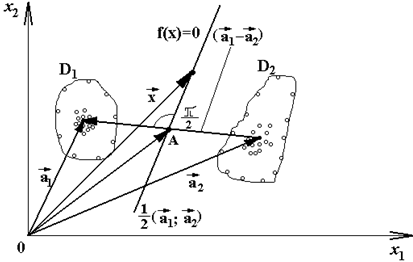
Рис.8. Приближенный способ построения разделяющей гиперплоскости

Так как точка А характеризуется вектором 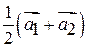, то уравнение разделяющей плоскости будет

.

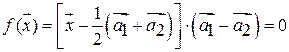Скалярное произведение вектора, лежащего в разделяющей плоскости, и вектора, нормального к ней, обращается в нуль.

Развертывая уравнение, находим

,

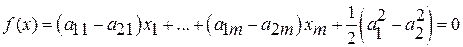где 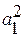и 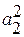– квадраты длины векторов 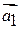и .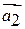

Сопоставляя последние два равенства, находим составляющие весового вектора:

; ;

; .

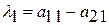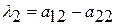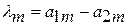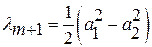Последние соотношения устанавливают приближенные значения компонентов весового вектора.