Множество рациональных чисел

Бесконечное множество Q, равномощное множеству натуральных чисел 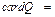æ₀ и

,

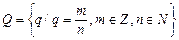называется множеством рациональных чисел.

Рациональное число вводится как отношение целого к натуральному числу. Рациональное число 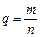определено не однозначно, поскольку числитель и знаменатель дроби можно домножить на одно и то же, не равное нулю число r, то есть 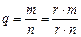, , 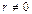. Если в знаменателе рационального числа стоит 1, то получаем целое число, то есть .

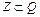Совокупность рациональных чисел упорядочена в отношении порядка «больше», «меньше» (см. неравенства в Z). Обладает свойством плотности, то есть , между p и q можно расположить бесконечно много рациональных чисел. Это дает возможность не только оценивать предметы количественно, но и проводить измерения с любой точностью, например отрезка прямой. Однако множество Q не обладает полнотой. Множество рациональных чисел, с точки зрения алгебры, есть коммутативное кольцо или поле.

Множество Q есть минимальное поле, в котором выполнимы алгебраические операции: , ,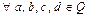

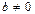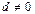
1) сложение: ;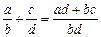

2) умножение: ;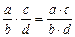

3) вычитание: ;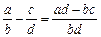

4) деление: , .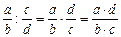

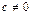Введено понятие степени числа и извлечение корня. 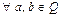и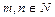

1) ;

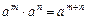2) , ;

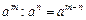3) ;

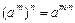4) ;

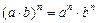5) , ;

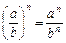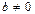6) , ;

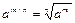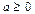в частности, если

7) ;

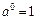8) .

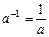Действие с корнями

1) ; , ;

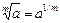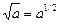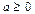2) ;

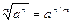3) ;

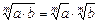4) , ;

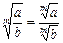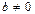5) ;

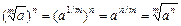6) .

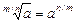Для упрощения вычислений, то есть сведéния умножения и деления к сложению и вычитанию, введено понятие логарифма.

Определение. Логарифмом числа b по основанию a называется показатель степени x, в которую нужно возвести основание, чтобы получить число b.

При 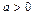, , 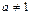, 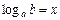где , .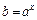

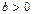Свойства.

Пусть , ,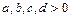

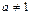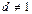
1) из определения, ;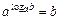

2) ;

3) ;

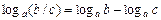4) , ;

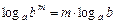5) , ;

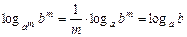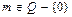6) , , ;

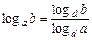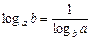7) ;

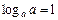8) .

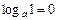Во множестве Q впервые введено понятие последовательности и ее предела. Геометрическая интерпретация рационального числа – точка на числовой прямой. Расстояние между двумя числами p и q определяется как .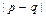

Несмотря на то, что рациональные числа плотно расположены на числовой прямой, их оказалось недостаточно для изучения непрерывно изменяющихся величин. Решение проблемы заключалось в заполнении пустоты, то есть во введении множества иррациональных чисел, которые добавлены к рациональным до непрерывности.