Выбор рациональных режимов работы устройств с точки зрения чувствительностей и погрешностей
При расчете характеристик устройств целесообразно определить зависимости чувствительностей и погрешностей не от величины удельной электрической проводимости, а от обобщенного параметра, куда входит величина s. Такой подход к решению задачи позволяет с помощью дискретного изменения частоты возбуждающего поля исследовать изделия с различными геометрическими характеристиками и физическими свойствами в оптимальных режимах.
| Таблица 6.1 – Результаты рассчитанных и измеренных величин амплитуд и фаз нормированных разностных ЭДС а2 = 11,3·10-3м | Вычисленные величины | φ, град | 38,3 | 35,4 | 34,6 | 34,6 | 36,0 | 36,3 | 48,7 | 35,7 | 36,6 |
| tgφ | 0,791465 | 0,710354 | 0,690582 | 0,690582 | 0,726957 | 0,735579 | 0,137684 | 0,718481 | 0,744351 | ||
| ׀λ∆Ф/Ф0׀ | 0,594 | 0,619 | 0,626 | 0,626 | 0,614 | 0,611 | 0,497 | 0,617 | 0,609 | ||
| х | 2,84 | 3,02 | 3,07 | 3,07 | 2,98 | 2,95 | 2,33 | 3,00 | 2,94 | ||
| Измеренные величины | φ, град | 38,0 | 35,1 | 34,7 | 35,0 | 36,4 | 36,8 | 48,8 | 35,7 | 36,5 | |
| λ∆Е/Е0 | 0,601 | 0,612 | 0,630 | 0,621 | 0,616 | 0,605 | 0,491 | 0,613 | 0,614 | ||
| λ | 1,670 | 1,668 | 1,668 | 1,665 | 2,077 | 2,077 | 4,398 | 4,413 | 4,421 | ||
| Е0,В | 0,869 | 0,289 | 0,1465 | 0,1135 | 0,112 | 0,127 | 0,770 | 0,500 | 0,226 | ||
| ∆Е,В | 0,313 | 0,106 | 0,0553 | 0,0423 | 0,0332 | 0,037 | 0,086 | 0,0695 | 0,0314 | ||
| Х0·10-3, м | 22,5 | 22,5 | 22,5 | 22,5 | 22,5 | 22,5 | 22,7 | 22,7 | 22,7 | ||
| ω, 1/с | 4200π | 340π | 140π | 110π | 440π | 500π | 7000π | 960π | 1040π | ||
| σ·107, См/м | 0,135 | 1,89 | 4,74 | 6,04 | 1,77 | 1,54 | 0,142 | 1,73 | 1,53 | ||
| R·10-3, м | 18,96 | 18,97 | 18,97 | 18,99 | 17,00 | 17,00 | 11,77 | 11,75 | 11,74 | ||
| Материал | Х18Н10Т | АМг 6 | Сплав меди | Сплав меди | Д16 | ЛС 63 | Х18Н10Т | Д16 | ЛС 63 |
Для определения дифференциальной чувствительности устройств, реализующих амплитудный и фазовый разностные методы, воспользуемся зависимостями, приведенными на рис.6.4 и 6.5. При этом формула для чувствительности устройства, основанного на амплитудных измерениях имеет вид
 , (6.39)
, (6.39)
где 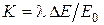 .
.
Поскольку при амплитудных измерениях предполагаются фиксированные значения λ и Е0, то, очевидно, что чувствительность Sk является одновременно и чувствительностью полезного сигнала ΔЕ к обобщенному параметру.
Производную dK/dx определим с помощью графического дифференцирования кривой рис.6.4 либо приближенно, причем Sk ≈ ΔK/Δx, где ΔK и Δx – приращения соответствующих величин в рабочей точке.
Чувствительность устройства на основе фазового разностного метода определяют по формуле
 , (6.40)
, (6.40)
где угол φвыбирается в рабочей точке. Расчет этой чувствительности проводят аналогично предыдущему случаю. Чувствительность Sφпредставляет собой чувствительность измерителя разности фаз к параметру х.
На рис.6.8, 6.9 показаны зависимости чувствительностей Sk и Sφ от величины х. Как видно, максимальные значениячувствительностей в обоих методах измерений наступают при х ≈ 1,6÷1,8. Такое совпадение значенийчувствительностей связано с наибольшей ответной реакцией изделия на внешнее поле, заключающейся в том, что производные амплитуды и фазы относительного разностного магнитного потока по обобщенному параметру имеют максимумы при данном х [21].

Рис.6.8 – Зависимость чувствительности разностных амплитудных
измерений σот величины х

Рис.6.9 – Зависимость чувствительности разностных фазовых измерений σ
от величины х
При описании разностных методов измерений удельной электрической проводимости было показано, что необходимо придерживаться определенной последовательности действий. Эту же последовательность нужно сохранить при определении погрешностей измерительных устройств. Действительно, погрешности измерений амплитуды и фазы разностной нормированной ЭДС приводят к погрешности определения х, которая, в свою очередь, вызывает ошибки в нахождении σ.
Поскольку в рассматриваемых случаях измерения носят косвенный характер и установлены функциональные связи между параметрами, то для нахождения погрешностей измерений σвоспользуемся классической методикой определения погрешностей косвенных измерений.
Обозначим зависимости, представленные на рис.6.4, 6.5, как
x = f1(K), (6.41)
x = f2(M), M = ctgj, (6.42)
Используя выражения (6.23), (6.24), (6.37), (6.41), (6.42) и результаты работы [13], получим выражения для оценки относительных значений погрешностей определения σ амплитудного и фазового разностных методов в случае косвенных измерений. Поскольку относительные погрешности параметров, входящие в выражения (6.23), (6.24), (6.31), (6.32), (6.37), (6.41) и (6.42), носят случайный характер и не зависят друг от друга, то, как указано в работе [13],более целесообразно оценивать погрешности косвенных измерений при доверительной вероятности 0,95, исходя из выражений
 ; (6.43)
; (6.43)
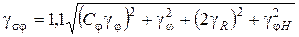 , (6.44)
, (6.44)
где γX0, γR, γΔЕ, γЕ0, γω, γφ – относительные значения погрешностей параметров, соответствующих указанным индексам;
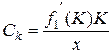 и
и 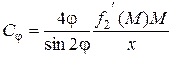
Ck и Сj – коэффициенты влияния; f1'(K) и f2'(M) – производные функций по аргументам, указанным в скобках (f1'(K) ≈ Δх/ΔК; f2'(M) ≈ Δх/ΔМ);
γкн и γφн – относительные значения погрешностей, связанные с небалансом ИК1 и ИК2 в отсутствие изделия. Последние составляющие погрешностей определяются отношениями абсолютных амплитудных и фазовых сигналов небалансов к соответствующим минимальным полезным сигналам. Для уменьшения погрешности γφH в отсутствие образца можно применить коррекцию угла φ→0, используя фазовращатель.
Если принять характерные численные значения относительных погрешностей измерений параметров электрической цепи, размеров изделия и координат, определяющих расположение датчика, таких как γX0 = 0,5 %; 0,2 %; γR = 0,5 %; γΔЕ = 0,5 %; γЕ0 = 0,5 %; γω = 0.1 %; γφ = 1 %; γkH = 0,2 %; γφH = 0,2 % и вычислить коэффициенты влияния в соответствующих точках функций (6.41), (6.42) и их производных, то получим зависимости γσK и γσφ от обобщенного параметра х. Эти зависимости приведены на рис.6.10, 6.11. Кривые 1 и 2 рис.6.10 рассчитаны для γX0 = 0,5 % и 0,2 %соответственно.
Результаты измерений амплитудным разностным методом дают монотонное возрастание значений погрешностей с увеличением параметра х. Это существенно ограничивает частотный диапазон амплитудных измерений с точки зрения точностных характеристик. Кроме того, как видно из рис.6.10, для уменьшения погрешности γσK необходимо достаточно точное определение величины расстояния X0. Требования к остальным допускам на точность установки первичного преобразователя (ИК1) относительно изделия являются менее жесткими.
Зависимость γσφ = f(x) имеет минимум погрешности при x ≈ 3,3. Для х > 3,3 погрешности измерений фазовым методом стремятся к постоянной величине, равной 2,5 %.При х < 3,3 наблюдается возрастание погрешности γσφ, связанное с ростом коэффициента влияния Сφ, так как φ→π/2.

Рисунок 6.10 – Зависимость погрешности разностных амплитудных измерений σ
от величины х

Рисунок 6.11 – Зависимость погрешности разностных фазовых измерений σ
от величины х
К преимуществам фазового метода следует отнести то, что на результаты измерений, как видно из выражения (6.32), не оказывают влияния геометрические размеры датчика, изделия и их взаимное расположение. Изменение указанных геометрических характеристик ограничено только порогом чувствительности измерителей фазовых сдвигов. Из графических зависимостей рис.6.8 – 6.11 видно, что амплитудный метод целесообразно применять тогда, когда необходимо определить значение σ, усредненное по объему изделия, что соответствует низким частотам возбуждающего магнитного поля (х ≤ 2). Определение же σ вблизи поверхности образца, как правило, представляет особый интерес, поскольку в этих областях вследствие воздействия на структуру материала различных видов обработок следует ожидать изменения величины удельной электрической проводимости по сравнению с σ внутренних слоев изделий.
Анализ точностных характеристик устройств для измерения удельной электрической проводимости σ показывает, что погрешности γσK и γσφ определяются положением рабочей точки кривых рис.6.4, 6.5, то есть величиной х и погрешностями используемых измерительных приборов. Отсюда следует, что представленные на рис.6.10, 6.11 кривые погрешностей носят универсальный характер и при указанных значениях относительных ошибок измерительной аппаратуры могут быть использованы для определения погрешностей измерений σ изделий с различными значениями радиусов и удельных электрических проводимостей, поскольку вариации последних при постоянной частоте приводят к изменению обобщенного параметра х, а, следовательно, и погрешностей измерений. Изменяя частоту внешнего магнитного поля, можно задавать рациональные режимы работы вихретоковых устройств с точки зрения достижения малых значений γσK и γσφ.
Сопоставление результатов расчетов чувствительностей и погрешностей измерений показывает, что при амплитудных измерениях оптимальный режим наступает при 0,5 < х < 2,0. В этом случае максимальной чувствительности соответствуют минимальные погрешности. Случай x < 0,5 приводит к существенному уменьшению чувствительности и возрастанию погрешностей, связанных со слабой реакцией изделия на возбуждающее поле.
Что же касается фазовых измерений, то рациональный по погрешностям режим наступает при х > 2 . При этом диапазоны изменения х, соответствующие минимальным погрешностям и максимальной чувствительности, не совпадают.
Погрешности измерений σ изделий можно уменьшить во всем диапазоне изменения х, если подобрать измерительную аппаратуру с более высокими классами точности по сравнению с используемой в рассматриваемых устройствах. При этом, однако, характер поведения кривых зависимостей погрешностей от х не изменится.
Выбор рациональных режимов накладывает определенные ограничения на частотный диапазон возбуждающего поля применительно к устройствам, основанным на обоих методах измерений. Эти ограничения связаны с параметрами преобразователя, изделия и измерительной аппаратуры. Верхний частотный предел для обоих методов связан с характеристиками преобразователя и ограничивается значением частоты f < 50 кГц (при этом на результатах измерений несущественно сказывается влияние паразитной распределенной емкости многослойных катушек). Требование к такой частоте накладывает, в свою очередь, ограничение на наименьший радиус исследуемого изделия. Например, при амплитудных измерениях на медном изделии (σ = 5,6·107 См/м) для х = 0,5 минимальное значение радиуса составит 0,11·10–3 м. В случае фазовых измерений для изделий из того же материала и х = 2 наименьший радиус изделия R = 0,43·10–3 м.
Для сравнительно массивных цилиндрических изделий ограничение по частоте возбуждающего поля связано с параметрами измерительной аппаратуры. Если принять характерный нижний предел по частоте f = 20 Гц для стандартных измерителей напряжения, то для цилиндрического изделия из нержавеющей стали с малым значениемσ = 0,135·107 См/м в случае оптимального режима х ≈ 2, наибольшее значение радиуса изделия соответствует 0,137 м. Для фазовых измерений, с точки зрения точности измерений, при частоте f = 20 Гц, практически нет ограничений на наибольший радиус цилиндрического изделия. Это дает возможность проводить измерения σ разностным фазовым методом трубчатых изделий с большим радиусом.
При работе устройств, реализующих предложенные методы измерений, могут возникать дополнительные погрешности измерений, связанные с воздействием внешних электромагнитных полей, взаимным влиянием КГР и КГК друг на друга, температурными нестабильностями, отклонением от однородности распределения магнитного поля по длине образца, со смещениями и перекосами изделия относительно измерительной катушки и другими факторами.
Воздействие внешних магнитных полей и взаимное влияние КГР и КГК друг на друга можно значительно уменьшить определенной ориентацией КГР и КГК в пространстве.
Температурная погрешность может быть также существенно уменьшена путем стабилизации намагничивающего тока и применения измерительных приборов со сравнительно большими входными сопротивлениями.
Оценку дополнительной погрешности, связанной с отклонением от однородного закона распределения напряженности магнитного поля вдоль образца, теоретически провести достаточно сложно. В данном случае удобно воспользоваться экспериментом. Результаты измерений показывают, что погрешности, связанные с размерами изделий и неоднородностью напряженности магнитного поля катушек Гельмгольца в объеме изделия, не превышают 1 % при l ≥ 2 Rк, а2 << Rк, 2R ≤ Rк/3, где l – длина цилиндрического изделия; Rк – средний радиус катушек Гельмгольца. При этом измерительная катушка располагается в области с высокой однородностью магнитного поля, то есть на продольной оси катушек Гельмгольца вблизи поверхности образца. В таком случае основной вклад в сигнал измерительной катушки будет определяться реакцией изделия на однородное магнитное поле.
Предлагаемые методы предназначены для измерения удельной электрической проводимости σ относительно длинных изделий и могут быть использованы для контроля качества изготовления и обработки прутков. В случае коротких изделий для обеспечения требуемой точности измерений необходимо проводить градуировку рассматриваемых устройств на образцах с известными значениями σи таких же размеров, как испытуемые.
Как было отмечено выше, изменение взаимного расположения ИК1 и изделия не оказывает влияния на результаты измерений только при использовании разностного фазового метода измерений. В других случаях изменение зазора и перекосы воздействуют на показания приборов. Оценки показывают, что угловой наклон датчика по отношению к направлению внешнего поля в пределах ± 5° вызывает дополнительную погрешность измерения σ около 0,5 %;смещение измерительной катушки вдоль оси Z на ±10 %по отношению к радиусу R приводит к погрешности измерений порядка 0,1 %.Влияние изменения положения изделия относительно измерительной катушки можно существенно уменьшить за счет использования двух пар диаметрально противоположно расположенных измерительных катушек.
Дата добавления: 2016-01-30; просмотров: 893;
