Теория работы преобразователя. Методы определения удельной электрической проводимости

Рассмотрим проникновение однородного переменного магнитного поля в цилиндрическое изделие (рис. 6.1). Все обозначения цилиндрической системы координат, размеры изделия и измерительной катушки ИК приведены на этом рисунке. Напряженность возбуждающего поля Н₀ направлена перпендикулярно к оси цилиндра. Такое направление внешнего поля возбуждает в изделии дипольный вихревой ток, который протекает вдоль координаты Y.

Для определения распределения напряженности магнитного поля в рассматриваемом случае воспользуемся уравнениями Максвелла, которые имеют вид

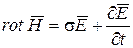, (6.1)

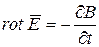, (6.2)

где Е – напряженность электрического поля; t – время; В – магнитная индукция; sЕ – плотность тока.

Примем общепринятые допущения, связанные с особенностями вихретокового контроля. Возбуждающее поле считается квазистационарным, и волновыми процессами в диэлектрической среде пренебрегают ввиду того, что размеры контролируемых изделий значительно меньше длины волны при используемых частотах внешнего поля. Так как напряженность магнитного поля невелика, то можно считать, что μ_r = const. Кроме того, предполагается, что материал изделия характеризуется постоянным значением удельной электрической проводимости σ.

Рисунок 6.1 – Изделие и измерительная катушка в поперечном однородном
магнитном поле

С учетом принятых допущений последним слагаемым в правой части уравнения (6.1) можно пренебречь.

В цилиндрической системе координат уравнения (6.1), (6.2) сводятся к системе уравнений

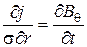, (6.3)

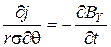, (6.4)

где j = σE_Y; B_θ, B_r, Е_Y – составляющие индукции и напряженности электрического поля вдоль соответствующих координат.

Продифференцировав уравнение (6.1) по времени и используя выражения (6.3), (6.4), получим дифференциальное уравнение для плотности продольного тока:

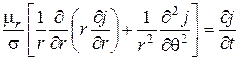. (6.5)

Решение этого уравнения для случая r ≤ R – получим в виде

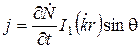, (6.6)

где 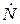комплексная константа; I₁ – модифицированная функция Бесселя первого рода; .

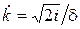Для случая r ≥ R электромагнитное поле является потенциальным, то есть удовлетворяет уравнению rot 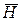= 0, или 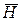= grad 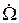, где потенциал 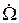находится из выражения

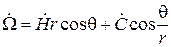. (6.7)

Здесь 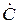– константа. В цилиндрической системе координат справедливы выражения

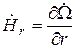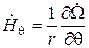, , (6.8)

где H_r и H_θ – составляющие напряженности магнитного поля. Граничные условия определяются соотношениями

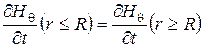; (6.9)

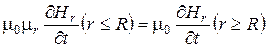. (6.10)

Используя (6.3), (6.4) и (6.8), получим

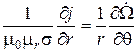, (6.11)

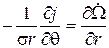. (6.12)

Подставив выражения (6.6) и (6.7) в уравнения (6.11) и (6.12) и решая эту систему при r = R, получим выражения для констант 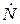и

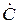
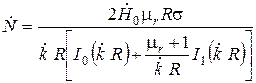, (6.13)

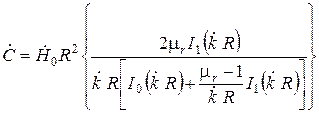, (6.14)

где I₀ – модифицированная функция Бесселя первого рода; H₀ – напряженность возбуждающего магнитного поля. В дальнейшем будем использовать понятие напряженности поперечного магнитного поля, выражение для которой имеет вид

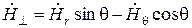. (6.15)

В итоге для области r ≤ R

, (6.16)

а для R ≤ r ≤ ∞

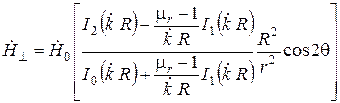, (6.17)

где I₂ – модифицированная функция Бесселя первого рода.

В практике неразрушающего контроля и измерений используется выражение для напряженности результирующего поперечного переменного магнитного поля снаружи изделия, так как оно характеризует реакцию цилиндрического объекта на возбуждающее внешнее поле.

Для немагнитного изделия (μ_r ≈ 1) выражение (6.17) упрощается и принимает вид [20]

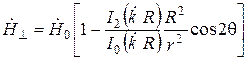, (6.18)

Характерной особенностью выражений для расчета внешней напряженности магнитного поля (формулы (6.17) и (6.18)) является зависимость величины 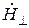от угловой координаты θ.

Величину внешнего результирующего магнитного потока можно определить из соотношения

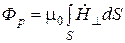, (6.19)

где S – площадь поверхности измерительной катушки ИК, которая пронизывается магнитным потоком.

Для того чтобы преобразователь измерял непосредственно реакцию цилиндрического изделия на внешнее возбуждающее поле, введем понятие разностного нормированного магнитного потока равного ( 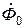– 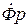)/ 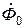, где 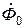– магнитный поток возбуждающего поля, пронизывающий измерительную катушку ИК в отсутствие изделия. Воспользовавшись выражениями (6.17), (6.18) и (6.19), получим формулу для определения этого потока, которая имеет вид

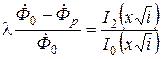, (6.20)

где λ – безразмерная геометрическая функция, которая зависит от формы, размеров датчика, цилиндрического изделия и их взаимного расположения; x – обобщенный параметр

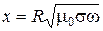. (6.21)

Конкретный вид геометрической функции λ определяется при интегрировании выражения (6.17) с учетом конечных размеров измерительной катушки, цилиндрического изделия и их взаимного расположения.

Для изделий с μ_r ≠ 1 соотношение для разностного нормированного магнитного потока будет иметь вид

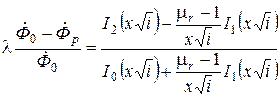
, (6.22)

Безразмерная геометрическая функция для круглой ИК, плоскость которой перпендикулярна к исходному магнитному полю, определяется выражением [21]

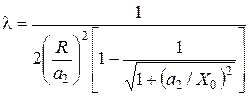, (6.23)

где а₂ – средний радиус ИК; Х₀ – расстояние от центра изделия до средины ИК. Расположение такой измерительной катушки и необходимые размеры показаны на рис.6.2, а. В случае прямоугольной измерительной катушки эта функция выражается соотношением

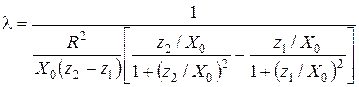, (6.24)

где z₁, z₂ и X₀ указаны на рис.6.2, б. Учитывая, что , из выражения (6.20) получим

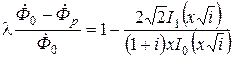, (6.25)

Пусть 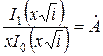, тогда модуль и фазу разностного нормированного магнитного потока можно записать в виде

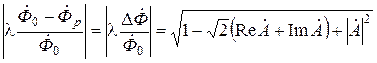, (6.26)

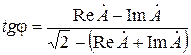, (6.27)

где 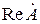, 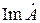и 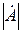– действительная, мнимая части и модуль комплексной величины 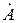; φ – угол сдвига фаз между потокам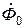и и – .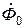

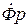Выразив 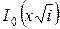и 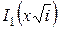через ber-, bei- функции нулевого и первого порядков, получим выражения для 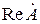, 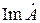и .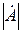

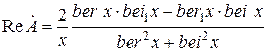; (6.28)

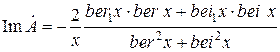; (6.29)

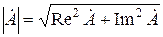. (6.30)

Рисунок 6.2 – Расположение круглой (а) и прямоугольной (б) измерительных
катушек вблизи изделия

На рис.6.3 приведены графические зависимости: кривая
1 – 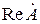= f(x); 2 – 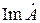= f(x) и 3 – 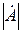= f(x).

Рисунок 6.3 – Зависимость реальной, мнимой частей и модуля 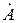от х

Подставив соотношения (6.28) – (6.30) в выражения (6.26) и (6.27) и учитывая, что 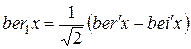и 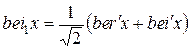, запишем формулу для модуля и фазы разностного нормированного магнитного потока в виде

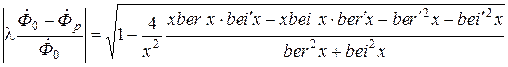, (6.31)

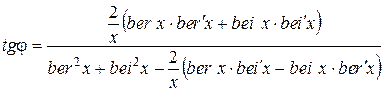, (6.32)

где знак "штрих" означает производную по аргументу.

На рис.6.4, 6.5 приведены графические зависимости 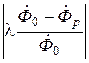= f(x) и ctg φ = f(x) соответственно. В практике возникает необходимость измерений на низких частотах и при малых радиусах (x ≤ 1) а также на высоких частотах и при больших радиусах (x ≥ 10) цилиндрических изделий. В этих случаях можно использовать приближенные формулы, получаемые разложением бесселевых функций в степенные ряды. Эти формулы имеют вид

для х ≤ 1

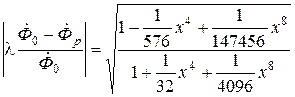, (6.33)

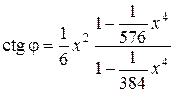, (6.34)

для x ≥ 10

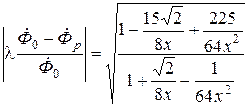, (6.35)

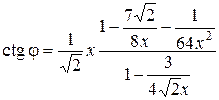, (6.36)

При построении кривой рис.6.5 использовалась функция ctg φ, поскольку эта зависимость практически линейна.

Рисунок 6.4 – Зависимость амплитуды разностного нормированного магнитного потока от величины обобщенного параметра

Рисунок 6.5 – Зависимость фазы разностного нормированного магнитного
потока от величины х

Так как в качестве аргумента применяется обобщенный параметр x, то представленные на рис.6.4, 6.5 зависимости являются универсальными и распространяются на цилиндрические изделия с различными величинами диаметров и удельных электрических проводимостей σ.

Полученные выше соотношения дают возможность установить определенную последовательность действий, необходимую для измерения величины σ. При этом возможны два случая.

Первый из них (амплитудный) состоит в том, что по измеренной величине разностной нормированной ЭДС, пропорциональной разностному нормированному магнитному потоку, и известной геометрической функции λ из графической зависимости рис.6.4 либо по таблице находят обобщенный параметр х. При использовании второго метода (фазового) по измеренному значению угла φ из графика рис.6.5 также находят параметр х. Величину удельной электрической проводимости σ при использовании как амплитудного, так и фазового методов рассчитывают по формуле

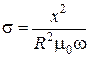. (6.37)

Следует отметить, что полученное значение σ соответствует величине продольной удельной электрической проводимости, поскольку при выбранном направлении напряженности возбуждающего поля она определяется зондирующими вихревыми токами, текущими вдоль образующей цилиндрического изделия.

Анализ выражений (6.31), (6.32) показывает, что фаза разностного нормированного магнитного потока φ не зависит от геометрической функции λ, то есть от размеров измерительной катушки, изделия и расстояния между ними. Это дает возможность проведения фазовых измерений и контроля удельной электрической проводимости изделий практически без отстройки от такого существенного мешающего фактора, как воздушный зазор между изделием и измерительной катушкой, что важно в практике неразрушающего контроля. В то же время амплитудные измерения удельной электрической проводимости требуют учета геометрических факторов (размеры датчика, изделия и их взаимное расположение).