Множества на основе отсортированных последовательностей

Изложенную выше реализацию теоретико-множественных операций (объединение. пересечение, разность) нельзя назвать блестящей с точки зрения производительности. Для каждого ключа одного множества происходит поиск путем полного перебора элементов в другом множестве. Если предположить, что количество элементов в первом и втором множестве приблизительно равны между собой и имеют значение N, то реализация таких операций потребует в худшем случае N2 сравнений ключей. Если множества содержат большое количество элементов, время выполнения операций основанных на полном переборе, может стать неприемлемо большим.

Производительность большинства операций со множествами можно значительно ускорить, если хранить значения строго по порядку, например, по возрастанию. Поскольку множество полностью контролирует процесс вставки очередного ключа, можно организовать работу таким образом, что новый элемент будет вставлен в нужной позиции без нарушения порядка возрастания:

voidIntegerSetInsertKey ( IntegerSet & _set, int_key )

{

// Если список пока пуст, вставить новый ключ в список

if( IntegerListIsEmpty( _set.m_data ) )

IntegerListPushBack( _set.m_data, _key );

Else

{

// Если новый ключ меньше первого узла, вставить новый ключ в начало списка

IntegerList::Node * pNode = _set.m_data.m_pFirst;

if( _key < pNode->m_value )

{

IntegerListPushFront( _set.m_data, _key );

return;

}

// Ищем узел, после которого нужно вставить новый ключ, не нарушив порядок

while( pNode )

{

// Игнорируем ключи, которые уже есть в множестве

if( pNode->m_value == _key )

return;

// Если текущий узел последний в списке,
// новый элемент вставляется в конец списка

else if( ! pNode->m_pNext )

{

IntegerListPushBack( _set.m_data, _key );

return;

}

// Если ключ в следующем узле больше нового ключа,

// нужно вставить новый ключ между текущим и следующим

else if( pNode->m_pNext->m_value > _key )

{

IntegerListInsertAfter( _set.m_data, pNode, _key );

return;

}

// Движемся далее

Else

pNode = pNode->m_pNext;

}

// Если ошибок нет, мы никогда не дойдем до этой точки

assert( ! "We should never get here" );

}

}

Сформировав таким образом упорядоченный во возрастанию список ключей, можно улучшить производительность поиска при переборе узлов. В частности, если искомый ключ меньше ключа в очередном обрабатываемом узле списка, то продолжать поиск не имеет смысла, т.к. в упорядоченном списке такого ключа уже точно не будет. Предположим, имеется множество из значений 10, 20, 30, 40, 50. Необходимо установить входит ли число 27 в состав множества. Значение 27 больше значений 10 и 20, однако меньше 30. Поскольку поиск доходит до большего значения 30, а значение 27 не найдено, дальнейший поиск не имеет смысла:

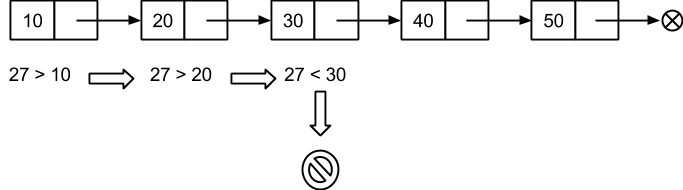
Улучшим процедуру поиска с учетом изложенного соображения:

boolIntegerSetHasKey ( constIntegerSet & _set, int_key )

{

IntegerList::Node * pNode = _set.m_data.m_pFirst;

while( pNode )

{

if( pNode->m_value == _key )

return true;

else if( pNode->m_value > _key )

return false;

pNode = pNode->m_pNext;

}

return false;

}

Аналогичным образом можно усовершенствовать операцию удаления ключа:

voidIntegerSetDeleteKey ( IntegerSet & _set, int_key )

{

IntegerList::Node * pNode = _set.m_data.m_pFirst;

while( pNode )

{

if( pNode->m_value == _key )

{

IntegerListDeleteNode( _set.m_data, pNode );

return;

}

else if ( pNode->m_value > _key )

break;

pNode = pNode->m_pNext;

}

assert( !"Key is unavailble!" );

}

Но наибольший эффект от упорядоченности можно получить именно при реализации теоретико-множественных операций. Например, алгоритм пересечения может быть реализован одновременным продвижением по внутренним спискам двух множеств со сравнением ключей в текущих узлах. Если находятся узлы с равными ключами, то такой ключ следует вставить в результирующее множество, в противном случае в зависимости от соотношения ключей следует перейти к следующему узлу в одном из списков. Предположим имеется два множества - с ключами { 10, 20 } и { 20, 30 } соответственно:

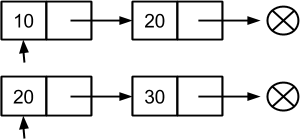
Начинаем процедуру сравнения узлов в двух списках с первых позиций. 10 < 20, соответственно, необходимо выбрать следующий узел в первом множестве:

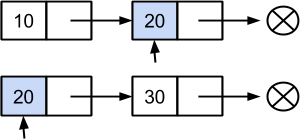
Сравнивая следующие элементы обнаруживаем, что в двух списках имеется значение 20. Заносим его в результирующее множество. Далее, передвигаемся к следующим узлам в обоих списках:

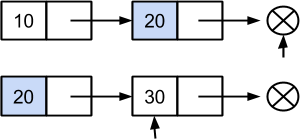
После этого действия первый список заканчивается, а значит других пересечений, кроме элемента {20} у данных множеств быть не может. Этим процедура пересечения и завершается.

Более точно этот алгоритм можно представить в виде следующего программного кода:

voidIntegerSetIntersect ( constIntegerSet & _set1,

constIntegerSet & _set2,

IntegerSet & _targetSet )

{

// Очищаем целевое множество

IntegerSetClear( _targetSet );

// Начинаем анализ с первых позиций в обоих списках одновременно

IntegerList::Node * pNode1 = _set1.m_data.m_pFirst;

IntegerList::Node * pNode2 = _set2.m_data.m_pFirst;

// Пересечение возможно, пока остаются узлы для рассмотрения в обоих списках

while( pNode1 && pNode2 )

{

// Если ключи в двух списках равны, этот ключ пересекается,

// и заносится в результирующее множество

if( pNode1->m_value == pNode2->m_value )

IntegerListPushBack( _targetSet.m_data, pNode1->m_value );

else if( pNode1->m_value < pNode2->m_value )

pNode1 = pNode1->m_pNext;

Else

pNode2 = pNode2->m_pNext;

}

}

Следует отметить, что при формировании результирующего множества непосредственно используются функции для внутренних списков, нежели функции для множеств, поскольку при таком способе обработки множество-результат автоматически будет заполняться уникальными элементами в строгом возрастающем порядке.

Аналогично можно представить реализации объединения и разности множеств:

voidIntegerSetUnite ( const IntegerSet & _set1,

const IntegerSet & _set2,

IntegerSet & _targetSet )

{

// Очищаем целевое множество

IntegerSetClear( _targetSet );

// Начинаем анализ с первых позиций в обоих списках одновременно

IntegerList::Node * pNode1 = _set1.m_data.m_pFirst;

IntegerList::Node * pNode2 = _set2.m_data.m_pFirst;

// Объединение возможно, пока остается хотя бы один узел в двух множествах

while( pNode1 || pNode2 )

{

// Имеются узлы для рассмотрения в обоих множествах

if( pNode1 && pNode2 )

{

// Если ключ в узле первого списка меньше ключа в узле второго списка,

// следует вставить ключ из первого множества

if( pNode1->m_value < pNode2->m_value )

{

IntegerListPushBack( _targetSet.m_data, pNode1->m_value );

pNode1 = pNode1->m_pNext;

}

// Если ключ в узле второго списка меньше ключа в узле первого списка,

// следует вставить ключ из второго множества

else if( pNode1->m_value > pNode2->m_value )

{

IntegerListPushBack( _targetSet.m_data, pNode2->m_value );

pNode2 = pNode2->m_pNext;

}

// Иначе - ключи в двух списках одинаковые. Следует вставить только 1 копию

Else

{

IntegerListPushBack( _targetSet.m_data, pNode1->m_value );

pNode1 = pNode1->m_pNext;

pNode2 = pNode2->m_pNext;

}

}

// Если элементов во втором множестве не осталось, копируем первое до конца

else if( pNode1 )

{

IntegerListPushBack( _targetSet.m_data, pNode1->m_value );

pNode1 = pNode1->m_pNext;

}

// Если же не осталось элементов в первом множестве, копируем второе до конца

Else

{

IntegerListPushBack( _targetSet.m_data, pNode2->m_value );

pNode2 = pNode2->m_pNext;

}

}

}

voidIntegerSetDifference ( constIntegerSet & _set1,

constIntegerSet & _set2,

IntegerSet & _targetSet )

{

// Очищаем целевое множество

IntegerSetClear( _targetSet );

// Начинаем анализ с первых позиций в обоих списках одновременно

IntegerList::Node * pNode1 = _set1.m_data.m_pFirst;

IntegerList::Node * pNode2 = _set1.m_data.m_pFirst;

// Разность возможна, пока остается хотя бы один узел в первом множестве

while( pNode1 )

{

// Если еще есть элементы во втором множестве, необходимо сравнивать ключи

if( pNode2 )

{

// Нельзя вставлять ключи, которые есть в обоих множествах

if( pNode1->m_value == pNode2->m_value )

{

pNode1 = pNode1->m_pNext;

pNode2 = pNode2->m_pNext;

}

// Если найден ключ в первом множестве, меньший ключу из второго,

// это означает его уникальность, следует внести ключ в результаты

else if( pNode1->m_value < pNode2->m_value )

{

IntegerListPushBack( _targetSet.m_data, pNode1->m_value );

pNode1 = pNode1->m_pNext;

}

// В противном случае нужно перейти к следующему элементу во втором м-ве

Else

pNode2 = pNode2->m_pNext;

}

Else

{

// Если второе множество закончилось, копируем элементы первого до конца

IntegerListPushBack( _targetSet.m_data, pNode1->m_value );

pNode1 = pNode1->m_pNext;

}

}

}

Такая реализация теоретико-множественных операций намного привлекательнее ранее описанной, поскольку в самом худшем случае осуществляет не более чем 2N сравнений, что существенно лучше квадратичной зависимости от N.