Теорема II.3 (Кронекера – Капелли).
Система линейных алгебраических уравнений совместна тогда и только тогда, когда ранг матрицы коэффициентов A равен рангу расширенной матрицы коэффициентов 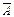 . Причем если ранг матрицы A равен рангу матрицы
. Причем если ранг матрицы A равен рангу матрицы 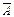 и равен числу неизвестных, то система уравнений имеет единственное решение; если ранги матриц A и
и равен числу неизвестных, то система уравнений имеет единственное решение; если ранги матриц A и 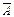 равны и меньше числа неизвестных системы, то система уравнений имеет множество решений (доказательство на стр. 82, теорема III.4).
равны и меньше числа неизвестных системы, то система уравнений имеет множество решений (доказательство на стр. 82, теорема III.4).
Методы решения СЛАУ
Рассмотрим систему из трех линейных алгебраических уравнений и трех неизвестных.
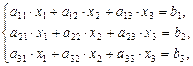 (II.5)
(II.5)
тогда матрица коэффициентов при неизвестных и расширенная матрица коэффициентов имеют вид:
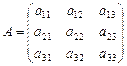 ,
, 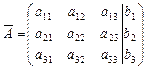 .
.
Метод Крамера
Для системы (II.5) введем следующие обозначения:
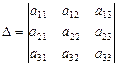 ,
, 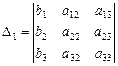 ,
,
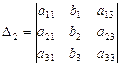 ,
, 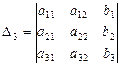 ,
,
где 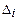 , i=1,2,3, – определители, полученные из исходного определителя D заменой i-ого столбца столбцом свободных членов.
, i=1,2,3, – определители, полученные из исходного определителя D заменой i-ого столбца столбцом свободных членов.
Тогда при решении системы методом Крамера [7] возможны следующие случаи:
1)если D¹0, то система (II.5) совместна и имеет единственное решение, которое находится по формулам:
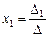 ,
, 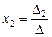 ,
, 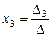 ;
;
2)если D=0, D1=D2=D3=0, то система (II.5) либо имеет множество решений, либо несовместна;
3)если D=0 и хотя бы один из D1, D2, D3 не равен нулю, то система (II.5) несовместна и решения не имеет.
Матричный метод
Пусть для системы (II.5) определитель D¹0. Запишем ее в матричной форме. Имеем: A – матрица коэффициентов при неизвестных, X – столбец неизвестных, B – столбец свободных членов системы:
 ,
,  ,
, 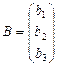 ,
,
тогда
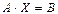 .
.
Так как умножение матриц не коммутативно (неперестановочно), то, чтобы получить в левой части равенства X, умножим это уравнение на 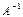 слева
слева
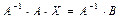 .
.
Так как, 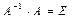 , то имеем
, то имеем
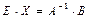
или
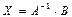 . (II.6)
. (II.6)
Метод Гаусса
Метод Гаусса основан на алгоритме последовательного исключения неизвестных. Выпишем расширенную матрицу коэффициентов системы (II.5):
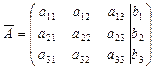 .
.
Задача состоит в том, чтобы привести ее к «треугольному» виду при помощи эквивалентных преобразований и получить единицы на главной диагонали и нули под ними.
Алгоритм состоит в том, что на каждом шаге выполняются следующие действия (количество шагов определяется количеством уравнений). Выбирается одна из ненулевых не рассмотренных ранее строк, ее номер считаем равным i. Все элементы этой строки делятся на элемент, стоящий на i-м месте (номер столбца этого элемента равен j). Если на i-м шаге какая-то из строк содержит уже на i-м месте единицу, то именно она переставляется и считается i-й строкой. Далее, добавляя к остальным, ранее не рассмотренным строкам i-ю строку умноженную на подходящее число, добиваемся того, что все элементы j-го столбца, расположенные ниже i-й строки, были равны нулю.
При решении систем алгебраических уравнений больших порядков требуется выполнять большой объем вычислений, в этом случае без техники не обойтись, следовательно, актуальной становится финансовая сторона вопроса.
Оценим число арифметических операций, необходимых для решения систем алгебраических уравнений порядка n методом Крамера. Будем учитывать только операции умножения и деления, поскольку времени на выполнение операций сложения и вычитания требуется на порядок меньше.
Для нахождения решения необходимо вычислить n+1 определитель порядка n, каждый из них содержит n! членов, пренебрегая операциями сложения и вычитания и учитывая, что для нахождения n неизвестных требуется n операций деления, окончательно получаем »(n+1)! операций. Поскольку у быстродействующей вычислительной техники программное обеспечение ориентировано на параллельную обработку информации (содержит параллельные программы), то время на выполнение вычислений может быть существенно уменьшено, но не более чем до n!.
Оценим число операций, необходимое для решения той же системы методом Гаусса. В первом уравнении этой системы n неизвестных, и для приведения к 1 всех коэффициентов в каждом из n уравнений требуется 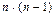 операций деления.
операций деления.
Для получения системы из n-1 уравнения требуется выполнить 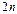 операций вычитания, пренебрегая которыми, получаем после 1-го шага
операций вычитания, пренебрегая которыми, получаем после 1-го шага 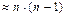 операций. Далее, по индукции, получаем
операций. Далее, по индукции, получаем 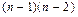 и т.д. до 2×1 операций, то есть окончательно
и т.д. до 2×1 операций, то есть окончательно
получаем
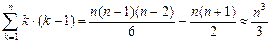 операций.
операций.
Таким образом, при больших n предпочтение, несомненно, должно быть отдано методу Гаусса. Часто по этой причине метод Гаусса называют машинным.
Плата за эффективность метода достаточно велика – это «неустойчивость» решения. Другими словами, правильность полученного решения системы методом Гаусса, вообще говоря, невозможно проверить.
При решении системы уравнений (II.5) методом Гаусса возможны следующие случаи.
1).Если матрица 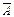 приведена к треугольному виду, то система (II.3) совместна и имеет единственное решение.
приведена к треугольному виду, то система (II.3) совместна и имеет единственное решение.
2).Если матрица 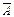 содержит хотя бы одну строку, все элементы которой равны нулю, то система (II.5) совместна и имеет множество решений.
содержит хотя бы одну строку, все элементы которой равны нулю, то система (II.5) совместна и имеет множество решений.
3).Если матрица 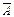 содержит строку, все элементы которой, кроме свободного члена, равны нулю, то система (II.5) несовместна, то есть решения не имеет.
содержит строку, все элементы которой, кроме свободного члена, равны нулю, то система (II.5) несовместна, то есть решения не имеет.
Пример II.8. Решить систему уравнений
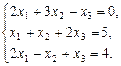
Решение. 1). Решим систему методом Крамера.
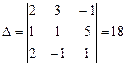 ,
, 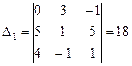 ,
,
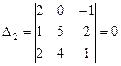 ,
, 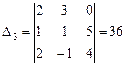 .
.
Так как D¹0, то система совместна и имеет единственное решение: 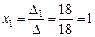 ,
, 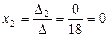 ,
,  .
.
2). Решим систему матричным методом.
Так как D¹0, то обратная матрица к матрице A существует. Вычислим алгебраические дополнения, имеем:
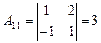 ; ;
| 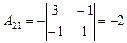 ; ;
| 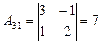 ; ;
|
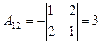 ; ;
| 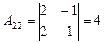 ; ;
| 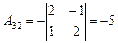 ; ;
|
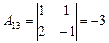 ; ;
| 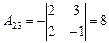 ; ;
| 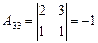 , ,
|
тогда обратная матрица 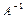 имеет следующий вид:
имеет следующий вид:
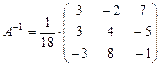 .
.
Найдем решение системы. Для этого запишем уравнение (II.6) в координатной форме:

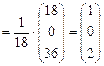 ,
,
следовательно, х1 = 1, х2 = 0, х3 = 2.
3). Решим систему методом Гаусса. Приведем расширенную матрицу коэффициентов 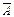 к “треугольному виду”. Для этого переставим 1-ю и 2-ю строки местами. Затем домножим 1-ю строку на (-2) и прибавим ко 2-й и 3-й строкам. Полученную 2-ю строку домножим на (3) и прибавим к полученной 3-й строке. В итоге последнюю строку разделим на 18.
к “треугольному виду”. Для этого переставим 1-ю и 2-ю строки местами. Затем домножим 1-ю строку на (-2) и прибавим ко 2-й и 3-й строкам. Полученную 2-ю строку домножим на (3) и прибавим к полученной 3-й строке. В итоге последнюю строку разделим на 18.
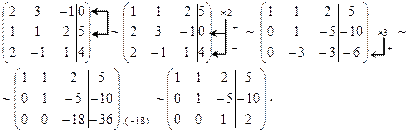 Матрица приведена к треугольному виду, следовательно, система совместна и имеет единственное решение. Найдем его, выписав систему уравнений, соответствующую последней матрице.
Матрица приведена к треугольному виду, следовательно, система совместна и имеет единственное решение. Найдем его, выписав систему уравнений, соответствующую последней матрице.
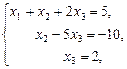 Þ
Þ 
Ответ: х1=1, х2=0, х3=2.
Пример II.9.
Решить систему уравнений
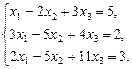
Решение.
1).Решим систему методом Крамера, имеем
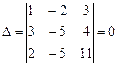 ,
, 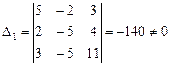 .
.
Так как D=0, D1¹0, то система несовместна, решения не имеет.
2).Решим систему матричным методом. Так как D=0, то обратная матрица к матрице A не существует, матричный метод неприменим.
3).Решим систему методом Гаусса. Приведем расширенную матрицу коэффициентов 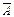 к треугольному виду. Для этого домножим 1-ю строку на (-3) и (-2) и прибавим ко 2-й и 3-й строкам соответственно. Полученную 2-ю строку прибавим к полученной 3-й строке.
к треугольному виду. Для этого домножим 1-ю строку на (-3) и (-2) и прибавим ко 2-й и 3-й строкам соответственно. Полученную 2-ю строку прибавим к полученной 3-й строке.
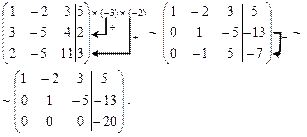
Так как у полученной матрицы, в последней строке, коэффициенты при неизвестных равны нулю, а свободный член не равен нулю, то решения нет, то есть система несовместна.
Ответ: система несовместна.
Однородная система линейных алгебраических уравнений (ОСЛАУ)
Определение. Система линейных алгебраических уравнений (СЛАУ) называется однородной, если все свободные члены системы равны нулю:
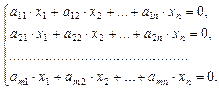 (II.7)
(II.7)
Очевидно, что однородная СЛАУ всегда совместна, так как одно ее решение всегда известно: все неизвестные равны нулю.
Теорема II.4. Однородная система (II.7) имеет единственное нулевое решение тогда и только тогда, когда определить матрицы коэффициентов при неизвестных не равен нулю. В противном случае система (II.7) имеет множество решений.
Пример II.10. Решить однородную систему уравнений

Решение.Вычислим определитель матрицы А:
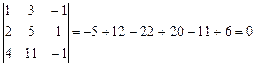 .
.
Так как 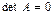 , то хотя бы одна из строк является линейной комбинацией других, следовательно, система имеет множество решений, которое найдем, например, методом Крамера.
, то хотя бы одна из строк является линейной комбинацией других, следовательно, система имеет множество решений, которое найдем, например, методом Крамера.
Решим систему из двух уравнений (оставшееся уравнение является комбинацией этих двух).
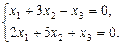
Пусть 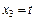 , тогда
, тогда
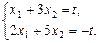
Вычислим определители
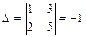 ,
, 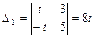 ,
, 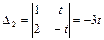 .
.
Тогда 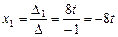 ,
, 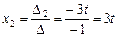 ,
, 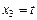 .
.
Ответ: 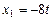 ,
, 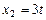 ,
, 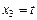 ,
, 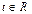 .
.
Дата добавления: 2016-01-26; просмотров: 1326;
