Аксиоматическое построение теории определителей
Определение. Определителем (детерминантом) квадратной матрицы 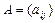 порядка n над ассоциативно-коммутативным кольцом K с единицей называется элемент кольца, равный сумме
порядка n над ассоциативно-коммутативным кольцом K с единицей называется элемент кольца, равный сумме 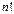 членов вида
членов вида
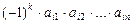 , (II.3)
, (II.3)
где 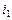 ,
, 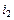 , …,
, …, 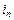 перестановки чисел 1, 2, 3, …, n, а k – число инверсий перестановки
перестановки чисел 1, 2, 3, …, n, а k – число инверсий перестановки 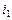 ,
, 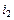 , …,
, …, 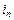 .
.
Для приложений наиболее важные случаи: K – числовое поле, K – кольцо многочленов.
Нам потребуются некоторые определения и факты, относящиеся к конечным множествам.
Пусть 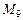 – множество, состоящее из всех цифр, кроме 0,
– множество, состоящее из всех цифр, кроме 0, 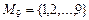 . Сколько различных девятизначных чисел можно составить из этих цифр, если они не повторяются? Очевидно, что если
. Сколько различных девятизначных чисел можно составить из этих цифр, если они не повторяются? Очевидно, что если 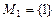 , то в этом случае имеет место только одно число 1, т.е. 1! вариантов; если
, то в этом случае имеет место только одно число 1, т.е. 1! вариантов; если 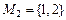 , то возможно только 2 варианта: 12 и 21, т.е. 2!; если
, то возможно только 2 варианта: 12 и 21, т.е. 2!; если 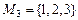 , то имеют место числа 123, 132, 213, 231, 312, 321, которых
, то имеют место числа 123, 132, 213, 231, 312, 321, которых 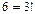 ; для
; для 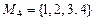 всего
всего 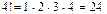 вариантов. Ясно, что из цифр множества
вариантов. Ясно, что из цифр множества 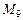 можно составить 9! чисел.
можно составить 9! чисел.
В общем случае, пусть 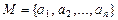 состоит из n различных элементов. Тогда число перестановок из всех элементов множества M, очевидно, равно n!. По определению положим
состоит из n различных элементов. Тогда число перестановок из всех элементов множества M, очевидно, равно n!. По определению положим 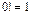 и
и 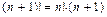 .
.
Пусть 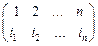 – подстановка, тогда если любые два числа поменять местами, то получим новую перестановку. Такое преобразование назовем транспозицией.
– подстановка, тогда если любые два числа поменять местами, то получим новую перестановку. Такое преобразование назовем транспозицией.
Все n! перестановок из n различных элементов можно расположить в таком порядке, что каждая следующая будет получаться из предыдущей одной транспозицией, причем начинать можно с любой перестановки.
Отсюда следует, что от любой перестановки из n элементов можно перейти к любой другой перестановке из тех же элементов при помощи нескольких транспозиций.
Будем говорить, что в данной перестановке числа i и j составляют инверсию, если 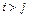 , но в перестановке i стоит раньше j.
, но в перестановке i стоит раньше j.
Перестановка называется четной, если ее элементы составляют четное число инверсий, и нечетной – в другом случае.
Например, перестановка 1, 2, …, n – четная, так как здесь число инверсий равно 0. Перестановка 1, 3, 5, 4, 2 – четная, так как для нее число инверсий равно 4.
Теорема. Всякая транспозиция меняет четность перестановки.
Следствие. При 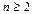 число четных перестановок из n элементов равно числу нечетных, то есть
число четных перестановок из n элементов равно числу нечетных, то есть 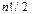 .
.
Пример II.4. В подстановке 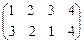 найти число инверсий для получения тождественной подстановки
найти число инверсий для получения тождественной подстановки 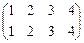 .
.
Ответ: три инверсии.
Положим, 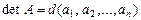 . Из определения следует,
. Из определения следует,
что множество определителей удовлетворяет условиям:
1) 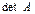 – линейная функция любой строки матрицы A:
– линейная функция любой строки матрицы A:
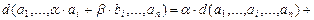
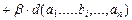 ;
;
2) если матрица B получена из A заменой строки 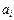 строкой
строкой 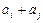 ,
, 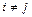 , то
, то 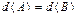 ;
;
3) 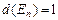 , где
, где 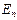 – единичная матрица размера n.
– единичная матрица размера n.
Условия 1) – 3) однозначно определяют аксиоматическое построение теории определителей.
Проверим свойства 1) – 3) на примере матрицы 3-го
порядка
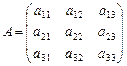 ,
, 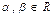 .
.
1) 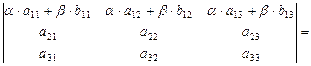
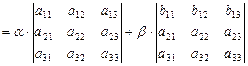 ;
;
2) к 1-й строке, умноженной на a, добавим 2-ю, умноженную на b:
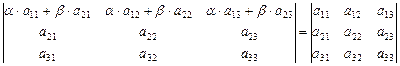 ;
;
3) 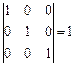 – очевидно.
– очевидно.
Пример II.5. Построить определитель третьего порядка.
Решение. Имеем 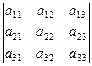 . Из определения следует, что число членов определителя равно 3!=6. Из следствия следует, что число четных инверсий равно числу нечетных. Рассмотрим подстановку
. Из определения следует, что число членов определителя равно 3!=6. Из следствия следует, что число четных инверсий равно числу нечетных. Рассмотрим подстановку 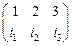 , из которой имеем
, из которой имеем 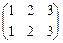 ,
, 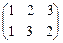 ,
, 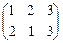 ,
, 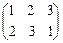 ,
, 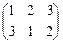 ,
, 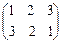 . Для первой подстановки из шести имеем член определителя
. Для первой подстановки из шести имеем член определителя 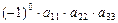 , для второй –
, для второй – 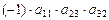 , далее
, далее 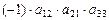 ,
, 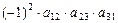 ,
, 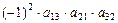 ,
, 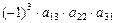 .
.
Таким образом, имеем
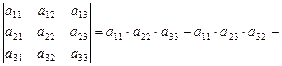
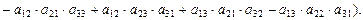
С точностью до слагаемых получили формулу (II.1).
Обратная матрица
Определение.Если определитель матрицы равен нулю, то матрица называется вырожденной. В противном случае квадратная матрица называется невырожденной.
Определение. Матрица 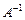 называется обратной к матрице A порядка n, если она удовлетворяет следующему равенству:
называется обратной к матрице A порядка n, если она удовлетворяет следующему равенству:
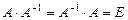 .
.
Теорема II.1. Для существования обратной матрицы 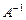 необходимо и достаточно, чтобы матрица A была невырожденной [3].
необходимо и достаточно, чтобы матрица A была невырожденной [3].
Если обратная матрица к матрице A порядка n существует, то она находится по формуле:
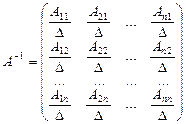 . (II.4)
. (II.4)
Пример II.6.
Найти матрицу, обратную к матрице 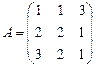 .
.
Решение. Вычислим определитель матрицы A.
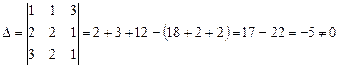 .
.
Так как D¹0, матрица A является невырожденной и для нее существует обратная, найдем ее. Для этого вычислим алгебраические дополнения для каждого элемента матрицы A:
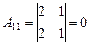 ; ;
| 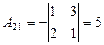 ; ;
| 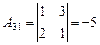 ; ;
|
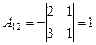 ; ;
| 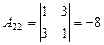 ; ;
| 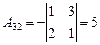 ; ;
|
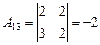 ; ;
| 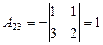 ; ;
| 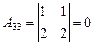 . .
|
Подставим найденные значения в формулу (II.4):
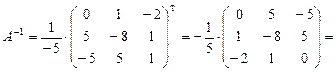
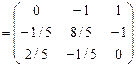 .
.
Ранг матрицы
Определение. Рангом матрицы A называется наивысший порядок ее миноров, отличных от нуля. Обозначается 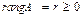 .
.
Дата добавления: 2016-01-26; просмотров: 2224;
