Системы линейных алгебраических неравенств
Определение. Два алгебраических выражения, соединенные одним из знаков <, >, £, ³, образуют неравенства. Неравенства называется линейными, если переменные x, y входят в него в первых степенях, не перемножаясь между собой, то есть имеют вид:
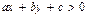 ,
, 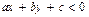 ;
;
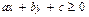 ,
, 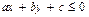 .
.
Решением линейного неравенства называется всякая пара значений переменных х, у, при которых оно выполнимо. Решить неравенство – значит найти множество всех его решений [2, 3].
Известно, что пара действительных чисел (x, y) однозначно определяет точку координатной плоскости, поэтому множество решений линейного неравенства можно изобразить графически на координатной плоскости. В зависимости от знака неравенства, графическим изображением решения линейного неравенства является одна из полуплоскостей, на которые разделяется плоскость соответствующей прямой.
Пусть задана система линейных неравенств:
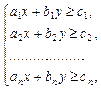
тогда решением этой системы называется упорядоченная пара чисел, удовлетворяющая каждому из неравенств этой системы, поэтому множество решений системы есть пересечение множеств решений входящих в нее неравенств. Если это пересечение пусто, то решения системы неравенств не существует.
Пример II.11. Изобразить на координатной плоскости множество решений неравенства 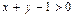 .
.
Решение. Преобразуем данное неравенство к виду 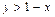 . Построим на координатной плоскости прямую
. Построим на координатной плоскости прямую 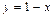 (рис. II.1).
(рис. II.1).
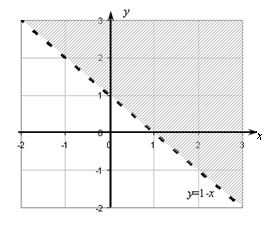
Рис. II.1
Так как ордината любой точки, лежащей выше прямой 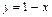 , больше, чем ордината точки, имеющей такую же абсциссу, но лежащей на прямой, то множество точек плоскости, расположенных выше этой прямой, и будет геометрическим изображением решений заданного неравенства.
, больше, чем ордината точки, имеющей такую же абсциссу, но лежащей на прямой, то множество точек плоскости, расположенных выше этой прямой, и будет геометрическим изображением решений заданного неравенства.
Пример II.12. Изобразить множество решений системы неравенств на координатной плоскости и определить координаты «угловых» точек этого множества.
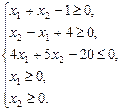
Решение. Построим на координатной плоскости прямые 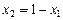 (1),
(1), 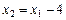 (2),
(2), 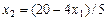 (3),
(3), 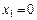 (4),
(4), 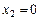 (5) (рис. II.2).
(5) (рис. II.2).
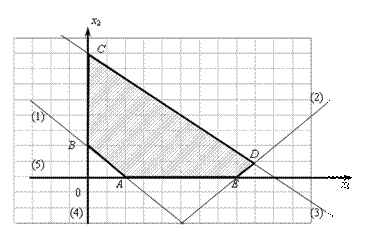
Рис. II.2
Все неравенства, входящие в систему, нестрогие, поэтому сами прямые будут входить в множество решений системы. Если неравенство имеет вид 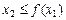 , то геометрическим изображением его решения является нижняя полуплоскость, если
, то геометрическим изображением его решения является нижняя полуплоскость, если 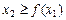 , то – верхняя полуплоскость.
, то – верхняя полуплоскость.
Угловые точки полученного множества лежат на пересечении двух прямых, поэтому, чтобы найти их координаты, необходимо решить системы уравнений, их задающих.
А: 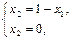
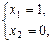 Þ
Þ 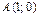 .
.
B: 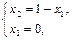
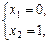 Þ
Þ 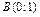 .
.
C: 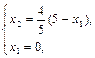
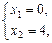 Þ
Þ 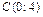 .
.
D: 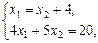
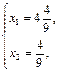 Þ
Þ 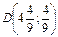 .
.
E: 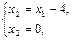
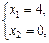 Þ
Þ 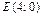 .
.
Дата добавления: 2016-01-26; просмотров: 2097;
