Интегральная теорема Лапласа
Как вычислить вероятность того, что событие А появится в  испытаниях не менее
испытаниях не менее 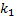 раз и не более
раз и не более 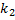 раз (для краткости будем говорить «от
раз (для краткости будем говорить «от 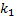 до
до 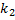 раз»)? На этот вопрос отвечает интегральная теорема Лапласа:
раз»)? На этот вопрос отвечает интегральная теорема Лапласа:
Теорема. Если вероятность наступления события А в каждом испытании постоянна и отлична от нуля и единицы, то вероятность 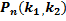 того, что событие А появится в
того, что событие А появится в 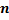 испытаниях от
испытаниях от 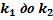 раз, приближённо равна определённому интегралу
раз, приближённо равна определённому интегралу 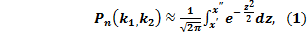 где
где 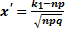 и
и 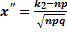 .
.
При решении задач, требующих применения интегральной теоремы Лапласа, пользуются специальными таблицами 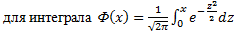 , т.к. неопределённый интеграл
, т.к. неопределённый интеграл 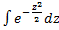 не выражается через элементарные функции. В таблице даны значения функции Ф(
не выражается через элементарные функции. В таблице даны значения функции Ф(  ) для положительных значении
) для положительных значении  и для
и для  =0. Для
=0. Для  <0 пользуются той же таблицей, учитывая, что функция Ф(
<0 пользуются той же таблицей, учитывая, что функция Ф(  ) нечётна, т.е. Ф(
) нечётна, т.е. Ф( 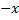 ) =
) = 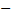 Ф(
Ф(  ). В таблице приведены значения интеграла лишь до
). В таблице приведены значения интеграла лишь до  =5, т.к. для
=5, т.к. для  >5 можно принять Ф(
>5 можно принять Ф(  ) = 0,5. Функцию Ф(
) = 0,5. Функцию Ф(  ) называют функцией Лапласа.
) называют функцией Лапласа.
Для того, чтобы можно было пользоваться таблицей функции Лапласа, преобразуем выражение (1) 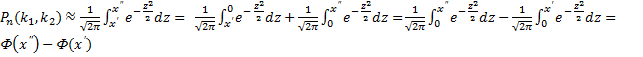 .
.
Итак, вероятность того, что событие А появится в 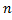 независимых испытаниях от
независимых испытаниях от 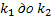 раз,
раз,
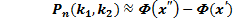 , где
, где 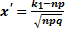 и
и 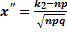 .
.
Случайные величины
Дата добавления: 2015-12-29; просмотров: 913;
