Формула полной вероятности. Пусть событие А может наступить при условии появления одного из несовместных событий , которые образуют полную группу

Пусть событие А может наступить при условии появления одного из несовместных событий 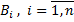, которые образуют полную группу. Пусть известны вероятности этих событий 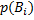и условные вероятности 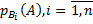события А. Требуется найти вероятность события А. На этот вопрос отвечает следующая теорема.

Теорема. Вероятность события А, которое может наступить лишь при условии появления одного из несовместных событий 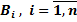, образующих полную группу, равна сумме произведений вероятностей каждого из этих событий на соответствующую условную вероятность события А:

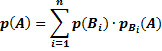
Доказательство. По условию теоремы, событие А может наступить, если наступит одно из несовместных событий 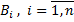, т.е. появление события А означает осуществление одного, безразлично какого, из несовместных событий 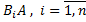. По теореме сложения = ) .

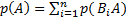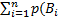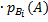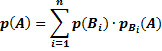
Эту формулу называют «формулой полной вероятности».

Формула Бейеса

Пусть событие A может наступить при условии появления одного из несовместных событий В₁, В₂, … , В_n , образующих полную группу. Поскольку заранее не известно, какое из этих событий наступит, их называют гипотезами. Допустим, что в результате испытания появилось событие А. Возникает задача, как изменились вероятности самих гипотез в результате наступления события А. Другими словами надо найти условные вероятности 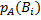, где .

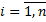По теореме умножения зависимых событий имеем

.

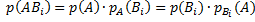Отсюда 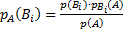, зная, что 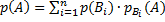, получим

.

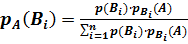Полученные формулы называютсяформулами Бейеса, которые позволяют переоценить вероятности гипотез после того, как становится известным результат испытания, в итоге которого появилось событие А.