Локальная теорема Лапласа
Формула Бернулли применяется, как правило, при небольших значениях  . Если число испытаний достаточно велико, то в этом случае применяется локальная теорема Лапласа:
. Если число испытаний достаточно велико, то в этом случае применяется локальная теорема Лапласа:
Теорема. Если вероятность появления события А в каждом испытании постоянна и отлична от нуля и единицы, то вероятность того, что событие А появится в 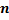 испытаниях ровно
испытаниях ровно 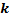 раз , приближённо равна значению функции
раз , приближённо равна значению функции
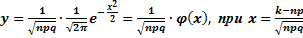 .
.
Имеются таблицы, в которых помещены значения функции 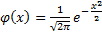 , соответствующие положительным значениям аргумента
, соответствующие положительным значениям аргумента  . Для отрицательных значений аргумента пользуются теми же таблицами, т.к. функция
. Для отрицательных значений аргумента пользуются теми же таблицами, т.к. функция 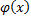 четна, т.е.
четна, т.е. 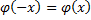 .
.
Итак, вероятность того, что событие А появится в  независимых испытаниях ровно
независимых испытаниях ровно 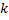 раз, приближённо равна
раз, приближённо равна
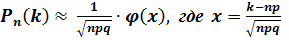 .
.
Формула Пуассона
Чуть изменим условие поставленной задачи, а именно, найти вероятность того, что при очень большом числе испытаний, в каждом из которых вероятность события очень мала ( 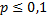 ), событие наступит ровно
), событие наступит ровно 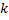 раз. В этих случаях (
раз. В этих случаях (  велико,
велико, 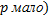 прибегают к асимптотической формуле Пуассона.
прибегают к асимптотической формуле Пуассона.
Сделаем важное допущение: произведение 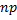 сохраняет постоянное значение, а именно,
сохраняет постоянное значение, а именно, 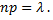 Воспользуемся формулой Бернулли для вычисления интересующей нас вероятности:
Воспользуемся формулой Бернулли для вычисления интересующей нас вероятности: 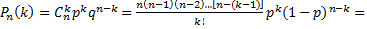 (т.к.
(т.к. 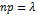 , то
, то 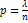 ) =
) = 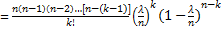 . Приняв во внимание, что
. Приняв во внимание, что  имеет большое значение, вместо
имеет большое значение, вместо 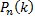 найдём
найдём 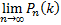 . При этом будет найдено лишь приближённое значение отыскиваемой вероятности:
. При этом будет найдено лишь приближённое значение отыскиваемой вероятности:  хотя и велико, но конечно, а при отыскании предела мы устремим
хотя и велико, но конечно, а при отыскании предела мы устремим  к бесконечности. Заметим, что поскольку произведение ,
к бесконечности. Заметим, что поскольку произведение , 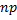 сохраняет постоянное значение, то при
сохраняет постоянное значение, то при 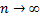 вероятность
вероятность 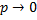 . Итак,
. Итак,
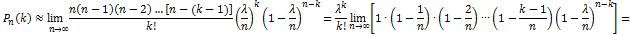
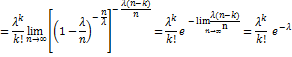
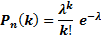
Дата добавления: 2015-12-29; просмотров: 1031;
