Математическое ожидание дискретной случайной величины
Математическим ожиданием дсв называют сумму произведений всех её возможных значений на их вероятности и обозначается 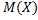 .
.
Если дсв задана законом распределения
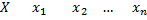
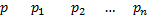 , то
, то
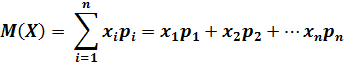
Пусть произведено  испытаний, в которых случайная величина
испытаний, в которых случайная величина 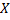 приняла
приняла 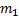 раз значение
раз значение 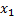 ,
, 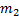 раз значение
раз значение 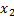 , …,
, …, 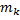 раз значение
раз значение 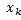 , причём
, причём 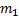 +
+ 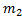 +…+
+…+ 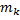 =
=  . Тогда сумма всех значений, принятых
. Тогда сумма всех значений, принятых 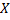 , равна
, равна 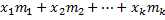 . Найдём среднее арифметическое
. Найдём среднее арифметическое 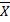 всех значений
всех значений 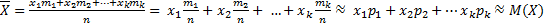 . Итак,
. Итак, 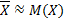 . Вероятностный смысл полученного результата таков: математическое ожидание приближённо равно среднему арифметическому наблюдаемых значений случайной величины.
. Вероятностный смысл полученного результата таков: математическое ожидание приближённо равно среднему арифметическому наблюдаемых значений случайной величины.
Математическое ожидание обладает следующими свойствами:
1. Математическое ожидание постоянной величины равно самой постоянной, т.е. 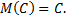
В самом деле, постоянную можно рассмотреть как дискретную случайную величину, которая имеет одно возможное значение 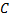 и принимает его с вероятностью
и принимает его с вероятностью 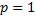 .
.
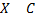
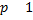
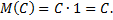
2. Постоянный множитель можно выносить за знак математического ожидания, т.е. 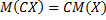 .
.


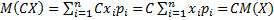 .
.
3. Математическое ожидание произведения двух независимых случайных величин равно произведению их математических ожиданий, т.е. 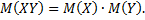
Если 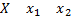
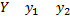 , то
, то 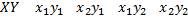
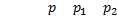
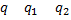
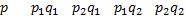
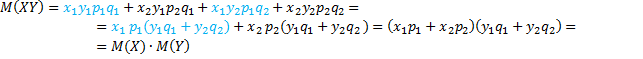
4. Математическое ожидание суммы двух случайных величин равно сумме математических ожиданий слагаемых, т.е. 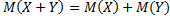 .
.
Если 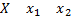
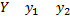 , то
, то 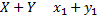
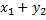
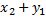
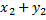
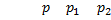
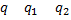
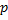
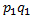
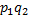
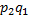
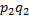
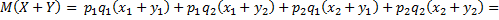
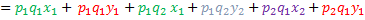 +
+ 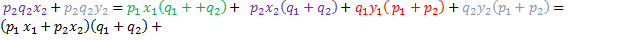
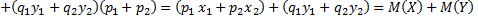 , т.к.
, т.к. 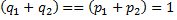 .
.
5. Математическое ожидание числа появлений события А в  независимых испытаниях равно произведению числа испытаний на вероятность появления события в каждом испытаний, т.е.
независимых испытаниях равно произведению числа испытаний на вероятность появления события в каждом испытаний, т.е. 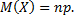
Дата добавления: 2015-12-29; просмотров: 879;
