Дисперсия дискретной случайной величины
Математическое ожидание, или среднее значение, случайной величины в ряде вопросов является достаточной характеристикой изучаемой случайной величины. Но бывает так, что одно среднее значение не даёт практически исчерпывающей характеристики случайной величины, а требуется ещё знать, сколь велики отклонения отдельных значений случайной величины от её математического ожидания.
Например, по данным статистического наблюдения изучается: средний рост или вес человека в определённой группе. Результаты опыта или наблюдения может считаться удачным, если возможные значения случайной величины незначительно отличаются от математического ожидания. Поэтому возникает необходимость введения ещё понятия отклонения случайной величины от её математического ожидания.
Отклонением называют разность между случайной величиной и её математическим ожиданием: 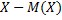 .
.
Это отклонение характеризует рассеяние случайной величины. На первый взгляд может показаться, что для оценки рассеяния проще всего вычислить все возможные значения отклонения случайной величины и затем найти их среднее значение, т.е. математическое ожидание отклонения.
Покажем, что математическое ожидание отклонения равно нулю. В самом деле 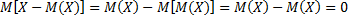 . Это объясняется тем, что одни возможные отклонения положительны, а другие – отрицательны; в результате их взаимного погашения среднее значение отклонения равно нулю. Эти соображения говорят о целесообразности заменить возможные отклонения их абсолютными значениями или их квадратами. В случае замены абсолютными значениями приходится оперировать с абсолютными величинами, что приводит иногда к серьёзным затруднениям. Поэтому чаще всего идут по другому пути, вычисляют среднее значение квадрата отклонения, которое и называют дисперсией.
. Это объясняется тем, что одни возможные отклонения положительны, а другие – отрицательны; в результате их взаимного погашения среднее значение отклонения равно нулю. Эти соображения говорят о целесообразности заменить возможные отклонения их абсолютными значениями или их квадратами. В случае замены абсолютными значениями приходится оперировать с абсолютными величинами, что приводит иногда к серьёзным затруднениям. Поэтому чаще всего идут по другому пути, вычисляют среднее значение квадрата отклонения, которое и называют дисперсией.
Дисперсией дискретной случайной величины называют математическое ожидание квадрата отклонения случайной величины от её математического ожидания и обозначают 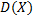 . Таким образом:
. Таким образом:
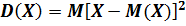
При решении практических задач часто пользуются немного видоизменённой формулой дисперсии, а именно: 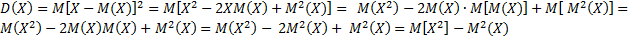 . При преобразовании было учтено, что математическое ожидание
. При преобразовании было учтено, что математическое ожидание 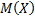 есть постоянная величина, а значит,
есть постоянная величина, а значит, 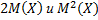 есть также постоянные величины. Итак,
есть также постоянные величины. Итак,
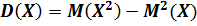
Дисперсия обладает следующими свойствами:
1. Дисперсия постоянной величины равна нулю, т.е. 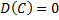 .
.
В самом деле 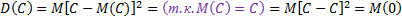 .
.
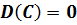 .
.
2. Постоянный множитель можно выносить за знак дисперсии, возводя его в квадрат, т.е. 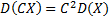 .
.
В самом деле 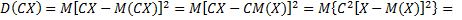
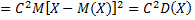 .
.
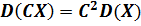 .
.
3. Дисперсия суммы двух независимых случайных величин равна сумме дисперсий этих величин, т.е. 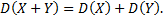
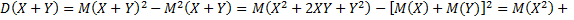
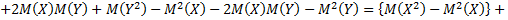
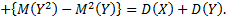
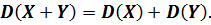
4. Дисперсия разности двух независимых случайных величин равна сумме их дисперсии, т.е. 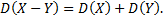
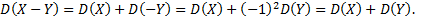
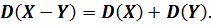
5. Дисперсия числа появления события А в 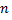 независимых испытаниях, в каждом из которых вероятность
независимых испытаниях, в каждом из которых вероятность 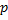 появления события постоянна, равна произведению числа испытаний на вероятности появления и непоявления события в одном испытании, т.е.
появления события постоянна, равна произведению числа испытаний на вероятности появления и непоявления события в одном испытании, т.е. 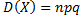 .
.
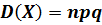 .
.
Дата добавления: 2015-12-29; просмотров: 1705;
