Вероятностный подход к измерению дискретной и непрерывной информации

В основе теории информации лежит предложенный Шенноном способ измерения количества информации, содержащейся в одной случайной величине, относительно другой случайной величины. Этот способ приводит к выражению количества информации числом.

Для дискретных случайных величин и , заданных законами распределения 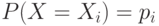, 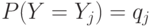и совместным распределением 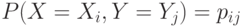, количество информации, содержащейся в относительно , равно

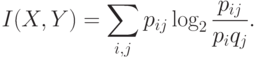
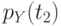Для непрерывных случайных величин, и , заданных плотностями распределения вероятностей , и 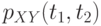, аналогичная формула имеет вид

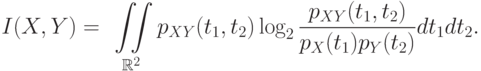
Очевидно, что

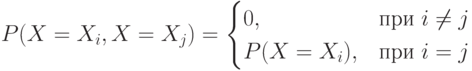
и, следовательно,

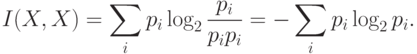
Энтропия дискретной случайной величины в теории информации определяется формулой

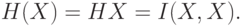
Свойства меры информации и энтропии:

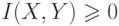, и независимы;

;

- константа;

, где ;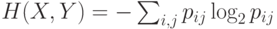

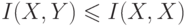. Если 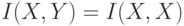, то - функция от . Если - инъективная функция1 от , то .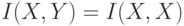

Логарифмированием из очевидного для всех 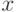неравенства 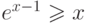(равенство устанавливается только при 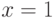) получается неравенство или .

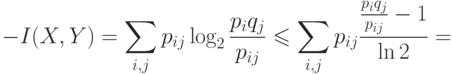
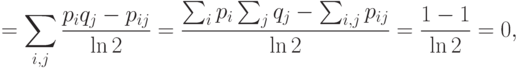
т.е. 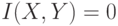только при 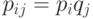для всех 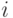и 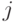, т.е. при независимости и . Если и независимы, то 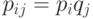и, следовательно, аргументы логарифмов равны 1 и, следовательно, сами логарифмы равны 0, что означает, что ;

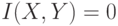Следует из симметричности формул относительно аргументов;

Если 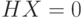, то все члены суммы, определяющей , должны быть нули, что возможно тогда и только тогда, когда - константа;

Из четырех очевидных соотношений

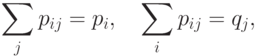
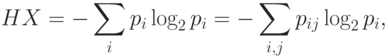
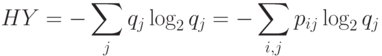
получается

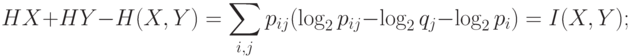
Нужно доказать 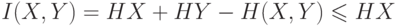или .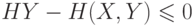

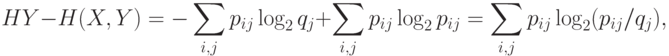
но 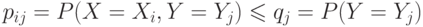, а значит аргументы у всех логарифмов не больше 1 и, следовательно, значения логарифмов не больше 0, а это и значит, что вся сумма не больше 0.

Если 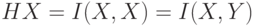, то для каждого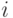 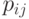равно либо 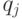, либо 0.

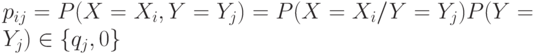Но из

следует

,

что возможно только в случае, когда -функция от .

При независимости случайных величин, и одна из них ничем не описывает другую, что и отражается в том, что для таких случайных величин, .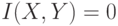

Рассмотрим пример измерения количества информации при подбрасывании двух игральных костей.

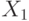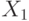Пусть заданы дискретные случайные величины , и . и 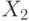- количества очков, выпавших соответственно на 1-й и 2-й игральной кости, а 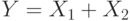. Найти , , .

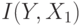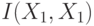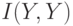Законы распределения вероятностей для дискретной случайной величины 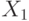и 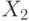совпадают, т.к. кости одинаковые и без изъянов.

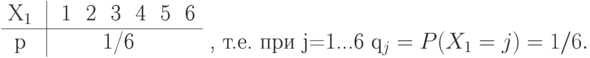
Закон распределения вероятностей для дискретной случайной величины ,

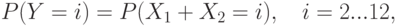
вследствие того, что 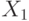, 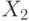- независимы и поэтому

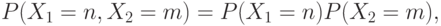
будет

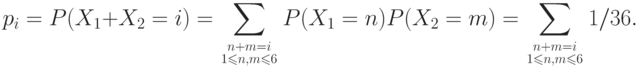
Таблицы, определяющие :

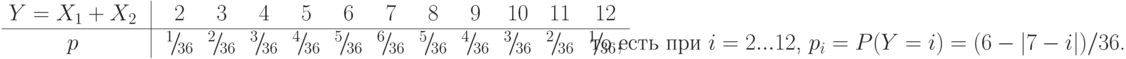
Закон совместного распределения вероятностей дискретной случайной величины 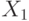и будет

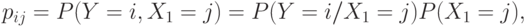
например,

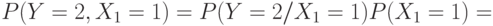
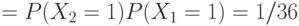. В общем случае получится

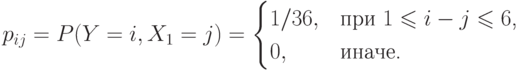
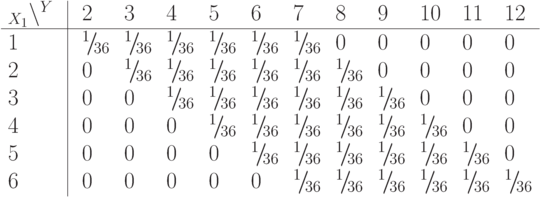
Тогда

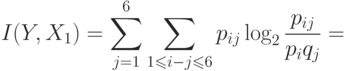
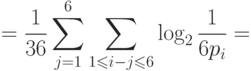
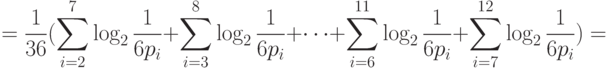
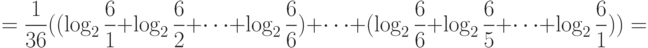
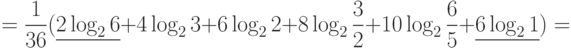
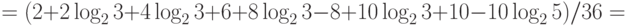
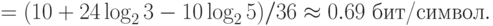
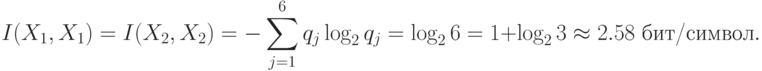
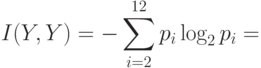
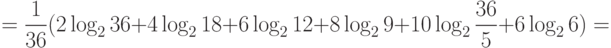
Здесь , что соответствует свойствам информации.

Подчеркнутый член 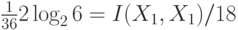в расчете 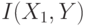соответствует информации о двух случаях из 36, когда 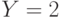и , которые однозначно определяют 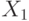. Шесть случаев, когда 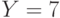, не несут никакой информации об 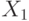, что соответствует подчеркнутому члену .

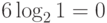Расчеты можно проводить, используя 4-е свойство информации, через энтропию.

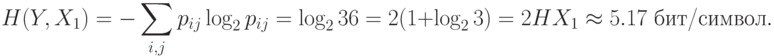
Расчет количества информации с использованием 4-го свойства, а не определения, обычно требует меньше вычислений.

Рассмотрим более простой пример. Пусть дискретная случайная величина равна количеству очков, выпавших на игральной кости, а дискретная случайная величина равна 0, если выпавшее количество очков нечетно, и 1, если выпавшее количество очков четно. Найти 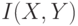и .

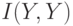Составим законы распределения вероятностей дискретной случайной величины и .

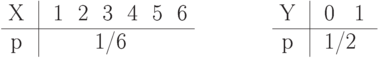
Таким образом, при 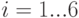и, соответственно, при .

Составим также закон совместного распределения вероятностей этих дискретных случайных величин

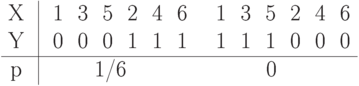
Таким образом,

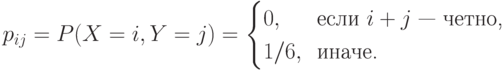
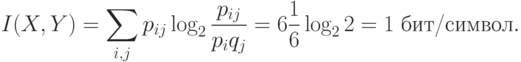
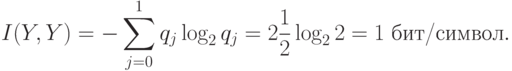
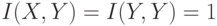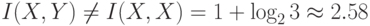Точное количество выпавших очков дает точную информацию о четности, т.е. 1бит. Из бит/сим и 3-го свойства информации следует, что информация об полностью определяет , но не наоборот, т.к. бит/сим. Действительно, функционально зависит от , а от функционально не зависит.

Расчеты через энтропию будут следующими

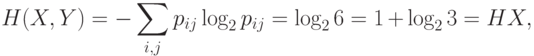
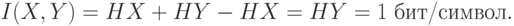
Упражнение 5 Найти энтропию дискретной случайной величины , заданной распределением

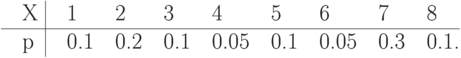
Упражнение 6 Значения дискретной случайной величины 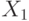и 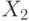определяются подбрасыванием двух идеальных монет, адискретная случайная величина равна сумме количества «гербов», выпавших при подбрасывании этих монет. Сколько информации об 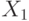содержится в ?

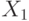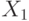Упражнение 7 Сколько информации об содержится в дискретной случайной величине , где независимые дискретные случайные величины и 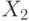могут с равной вероятностью принимать значение либо 0, либо 1? Найт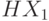и и 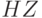. Каков характер зависимости между 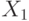и ?

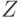Упражнение 8 Дискретные случайные величины 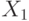, 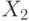- зависимы и распределены также как и соответствующие дискретные случайные величины из предыдущей задачи. Найти 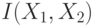, если совместное распределение вероятносте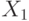й и 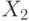описывается законом

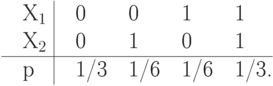
Упражнение 9 Дискретные случайные величины 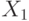и 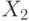определяются подбрасыванием двух идеальных тетраэдров, грани которых помечены числами от 1 до 4. дискретная случайная величина равна сумме чисел, выпавших при подбрасывании этих тетраэдров, т.е. 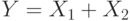. Вычислить 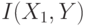, 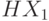и .

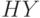Упражнение 10 Подсчитать сколько информации об 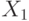содержится в дискретной случайной величине 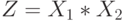, а также 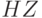. Дискретные случайные величины 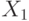и 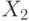берутся из предыдущего упражнения.

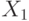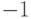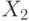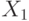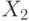Упражнение 11 Дискретная случайная величина может принимать три значения , 0 и 1 с равными вероятностями. Дискретная случайная величина с равными вероятностями может принимать значения 0, 1 и 2. и - независимы. 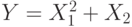. Найти , , , , .

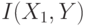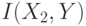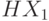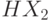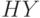Упражнение 12 Найти энтропии дискретных случайных величин , , 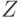и количество информации, содержащейся в 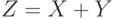относительно . и - независимы и задаются распределениями

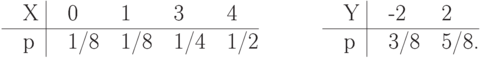
Энтропия д.с.в. - это минимум среднего количества бит, которое нужно передавать по каналу связи о текущем значении данной д.с.в.

Рассмотрим пример (скачки). В заезде участвуют 4 лошади с равными шансами на победу, т.е. вероятность победы каждой лошади равна 1/4. Введем д.с.в. , равную номеру победившей лошади. Здесь 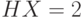. После каждого заезда по каналам связи достаточно будет передавать два бита информации о номере победившей лошади. Кодируем номер лошади следующим образом: 1-00, 2-01, 3-10, 4-11. Если ввести функцию 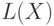, которая возвращает длину сообщения, кодирующего заданное значение , то м. о. 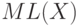- это средняя длина сообщения, кодирующего . Можно формально определить 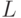через две функции , где каждому значению ставит в соответствие некоторый битовый код, причем, взаимно однозначно, а возвращает длину в битах для любого конкретного кода. В этом примере .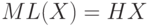

Пусть теперь д.с.в. имеет следующее распределение

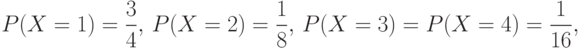
т.е. лошадь с номером 1 - это фаворит. Тогда

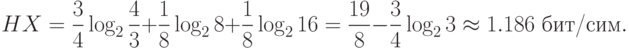
Закодируем номера лошадей: 1-0, 2-10, 3-110, 4-111, - т.е. так, чтобы каждый код не был префиксом другого кода (подобное кодирование называют префиксным ). В среднем в 16 заездах 1-я лошадь должна победить в 12 из них, 2-я - в 2-х, 3-я - в 1-м и 4-я - в 1-м. Таким образом, средняя длина сообщения о победителе равна 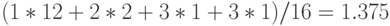бит/сим или м. о. 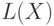. Действительно, 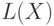сейчас задается следующим распределением вероятностей: , , . Следовательно,

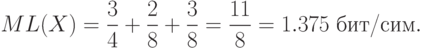
Итак, .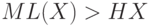

Можно доказать, что более эффективного кодирования для двух рассмотренных случаев не существует.

То, что энтропия Шеннона соответствует интуитивному представлению о мере информации, может быть продемонстрировано в опыте по определению среднего времени психических реакций. Опыт заключается в том, что перед испытуемым человеком зажигается одна из лампочек, которую он должен указать. Проводится большая серия испытаний, в которых каждая лампочка зажигается с определенной вероятностью 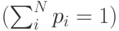, где 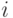- это номер лампочки. Оказывается, среднее время, необходимое для правильного ответа испытуемого, пропорционально величине энтропии 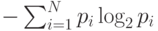, а не числу лампочек 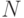, как можно было бы подумать. В этом опыте предполагается, что чем больше информации будет получено человеком, тем дольше будет время ее обработки и, соответственно, реакции на нее.

Упражнение 13 Найти энтропию д.с.в. и среднюю длину каждого из приведенных кодов для этой д.с.в.

Упражнение 14 д.с.в. равна количеству «гербов», выпавших на двух идеальных монетках. Найти энтропию . Придумать минимальный код для , вычислить его среднюю длину и обосновать его минимальность.

Упражнение 15 д.с.в. задана распределением , 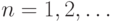Найти энтропию этой д.с.в. Придумать минимальный код для , вычислить его среднюю длину и обосновать его минимальность.

Упражнение 16 Про д.с.в. известно, что ее значениями являются буквы кириллицы. Произведен ряд последовательных измерений , результат которых - «ТЕОРИЯИНФОРМАЦИИ». Составить на основании этого результата приблизительный закон распределения вероятностей этой д.с.в. и оценить минимальную среднюю длину кодов для .