Условие Найквиста для минимума межсимвольной интерференции
Проблема повышения удельной скорости передачи данных была предметом напряженных исследований. Можно, например, менять форму импульса, который ставится в соответствие передаваемому двоичному знаку. Для того, чтобы повысить скорость передачи можно потребовать, чтобы воздействие соседних импульсов было сведено к нулю лишь в моменты отсчета значений принятого сигнала (0, T, 2T, 3T…). Это требование называется первым условием Найквиста. Импульс, соответствующий этому условию, обеспечивает отсутствие межсимвольных искажений. Такой импульс известен, его форма приведена . Если, например, в момент времени t=0 должен передаваться единичный двоичный символ, то в канал связи отправляется импульс g(t). В моменты времени (0, T, 2T, 3T…) значения импульса равны нулю, следовательно, в эти моменты могут передаваться следующие двоичные знаки, причем по Найквисту их прием не будет сопровождаться межсимвольной интерференцией. Скорость передачи данных равна 1/T (бит/с). Амплитудный спектр импульса, соответствующего первому условию Найквиста. Ширина полосы частот, занимаемой этим импульсом, равна 1/2T (Гц). Таким образом, спектральная эффективность данных равна Sn=2(бит/с)/Гц. Это предел удельной скорости передачи данных с помощью двухпозиционных (двухуровневых) импульсов, называемый иногда «барьером Найквиста». И мало в каких работах оговаривается при каком значении Eb/No и вероятности ошибки. Увы, ниже 2.5dB при Pe=10e-5 работ не обнаружено.
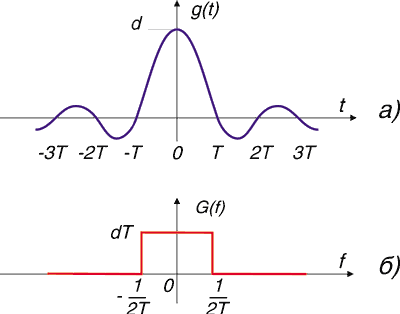
Все без исключения работы в связи рассматривают методы получения импульса, показанного выше. Он соответствует выходному сигналу идеального фильтра нижних частот, на вход которого подан прямоугольный импульс бесконечно малой длительности. Но идеальный фильтр нижних частот не реализуем, задержка сигнала в нем была бы равна бесконечности. Но даже если бы импульс в форме можно было бы сформировать, то его нельзя было бы использовать на практике. Причину этого обстоятельства можно объяснить с использованием глазковой диаграммы. Вертикальное раскрытие глазка в случае использования импульсов, соответствующих первому условию Найквиста, равно максимальному, что и означает отсутствие межсимвольных искажений. Однако горизонтальное раскрытие глазка стремится к нулю. При самом незначительном отклонении моментов отсчета межсимвольные искажения становятся столь большими, что восстановление значений передаваемых данных невозможно. Значение условия Найквиста и соответствующего ему импульса заключается в установлении ориентира, к которому должны стремиться разработчики систем связи. Увы идя заведомо по ложному пути.
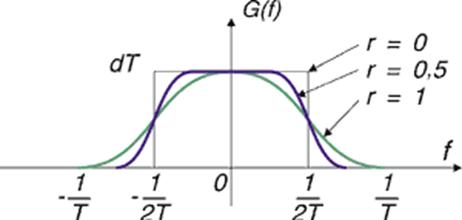
Сравнительно простыми средствами удается добиться достижения удельной скорости передачи данных, составляющей 30-50% от «барьера Найквиста». Один из способов - сглаживание прямоугольной формы спектральной плотности импульса по косинусоидальному закону и соответственно небольшое изменение формы импульса, связанное с уменьшением колебаний импульса за пределами интервала (-T...+T). Но все таки была обнаружена одна интересная работа:
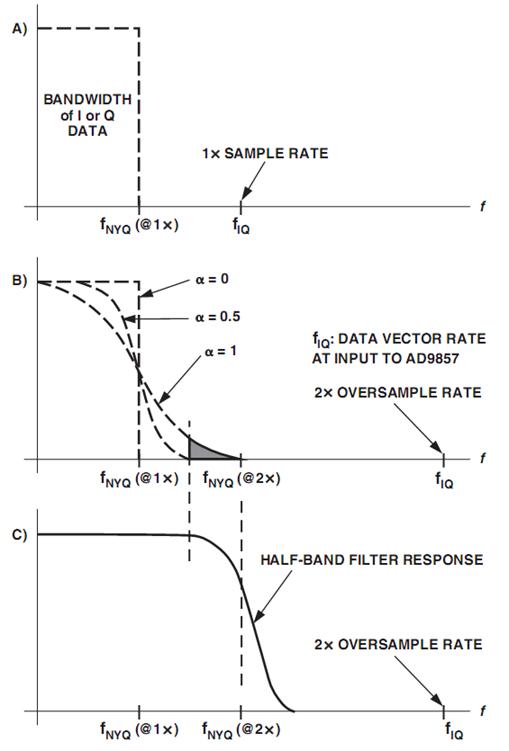
В работе [7]:
Утверждается, что из-за уменьшения коэффициента сглаживания меньше 1, передача по квадратурному каналу без МСИ невозможна. Заштрихованная область «хвоста» АЧХ не проходит через канал при а=0.5. Поэтому рекомендуется канальные фильтры выбирать с частотой среза 2Fn (а=1). Хотя битовая скорость в QI каналах в 2 раза ниже! Это очень серьезное замечание требующее специального исследования. Как на самом деле выбирать фильтры передачи и приема в основной не модулированной полосе? Ведь если уж тут ошибка (до реальных помех в эфире), то применение цифровых методов борьбы с групповыми (перемежение) и одиночнымы ошибками (турбосверточные кодеки) сводит всёна нет. Мы всю мощь цифровой борьбы с ошибками фактически тратим на собственную инженерную ошибку элементарного проектирования в основной не модулированной полосе частот!
Интересно, что «барьер Найквиста» не является такой абсолютной границей, как, например, пропускная способность канала связи, задаваемая формулой Шеннона:
C=Fx log2(1+Ps/Pn),
где C - предельная скорость передачи информации, или пропускная способность канала связи с шириной полосы пропускания F и отношением мощности сигнала к мощности шума на выходе канала Ps/Pn.
(Не следует путать скорость передачи информации со скоростью передачи данных, хотя размерности этих величин и одинаковые - бит/с. О понятии «информация» см.: 625. 1997, № 7, с. 60).
Пропускная способность канала, или «граница Шеннона», не может быть превышена - при приближении скорости передачи информации к теоретическому пределу необходимо существенно усложнять способы кодирования передаваемых данных. Формула Шеннона подсказывает и принцип преодоления «барьера Найквиста» - увеличение отношения мощности сигнала к мощности шума. Чем больше это отношение, тем в меньшей полосе могут быть переданы данные. А конкретным способом преодоления барьера может быть переход к многопозиционным (многоуровневым) сигналам, которые можно применять при большой мощности сигнала без риска увеличить вероятность ошибки при определении величины принимаемого сигнала. Однако зависимость пропускной способности от мощности сигнала является логарифмической, поэтому преодолевать «барьер Найквиста» достаточно трудно (необходимая мощность сигнала как функция скорости передачи данных растет по экспоненциальному закону).
Профессор. Л.М. Финк в интересной книге «Сигналы, помехи, ошибки.» сравнивает «барьер Найквиста» в технике связи со звуковым барьером в авиации. Достичь скорости звука и превзойти ее оказалось возможным, но для этого потребовались десятилетия труда ученых и инженеров. Границу Шеннона можно тогда было бы сравнить со скоростью света.
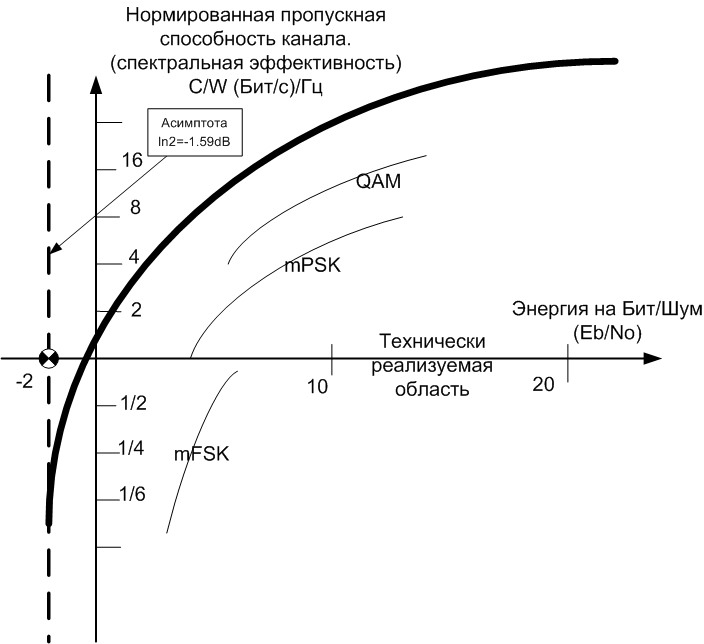
Формула Шеннона дает ясное представление о границе реализуемости систем цифровой передачи. Техническая область реальных устройств всегда ниже теоретического отношения С/W (скорость / полоса). С другой стороны есть зависимость спектральной эффективности от отношенияEb/No (энергия бита/энергия шума). Нужно обязательно это учитывать. Так как отношение сигнал/шум связано с отношением Eb/No через спектральную эффективность, а максимально возможная помехоустойчивость достигается только в одном случае, если сигналы ортогональны и противоположны одновременно (по Котельникову, это принцип потенциальной помехоустойчивости).
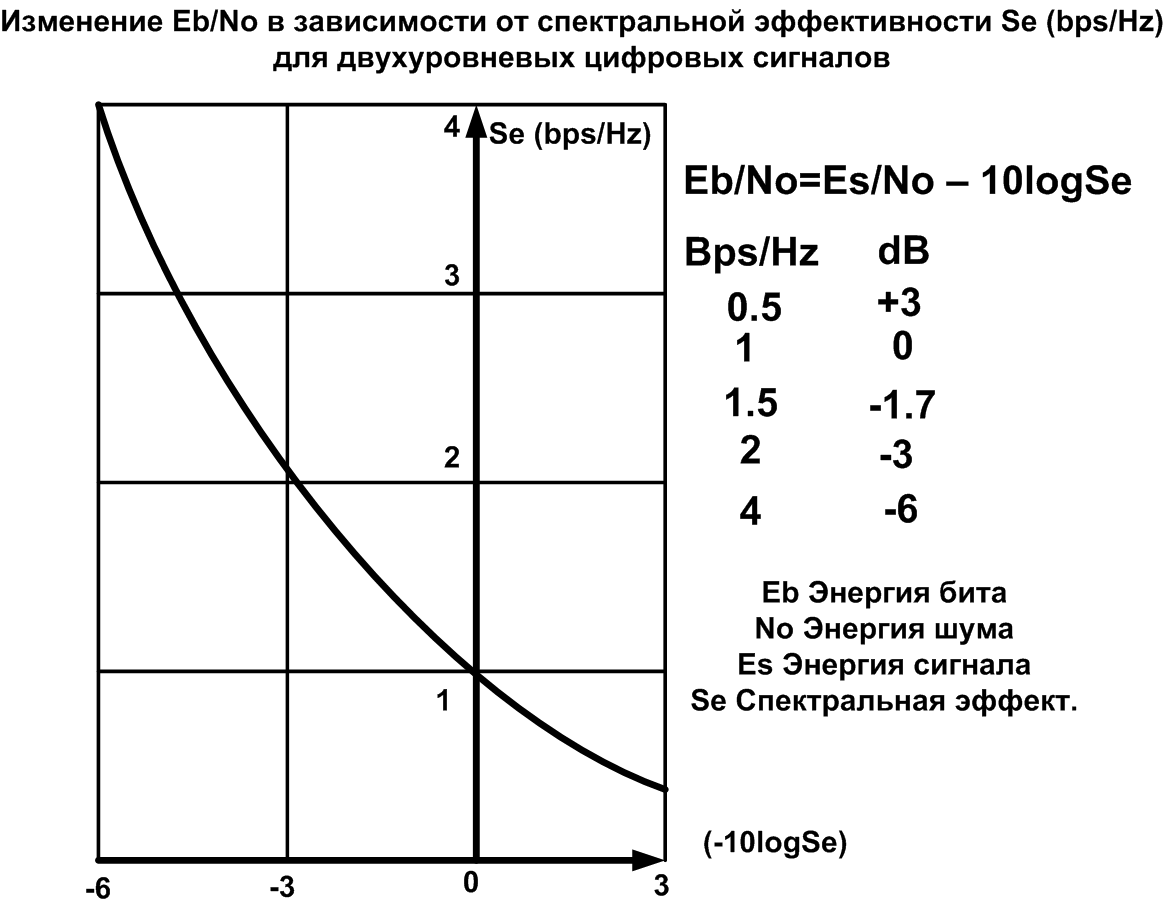
Заметки по применению GMSK модема FX589. (материал для помощи в понимании проблемы)
Начало перевода:
Самый простой способ передачи данных по FM радио заключается в сдвиге RF несущей в одну сторону для представления логической ‘1’ и в другую сторону для представления логического ‘0’. Такой прямой метод известен как манипуляция частотным сдвигом (FSK); FSK может быть успешным, но предъявляет требования на очень широкую полосу передачи. Для уменьшения полосы входные данные перед модуляцией могут быть пропущены через фильтр с низкочастотной фильтрацией специальной формы. Одним из эффективных методов является Гауссова манипуляция с минимальным сдвигом (GMSK). [6]
GMSK это метод модуляции данных для передачи данных с высокой скоростью в узкополосных каналах FM радио. В своей простейшей формеGMSK включает в себя прохождение цифрового потока данных через Гауссовый фильтр перед их подачей на вход частотного модулятора
Гауссовый фильтр это низкочастотный элемент который при возбуждении на его импульсом на выходе выдает сигнал в виде Гауссовой кривой.

Ниже представлено движение потока данных в системах FM радио использующих GMSK модем:
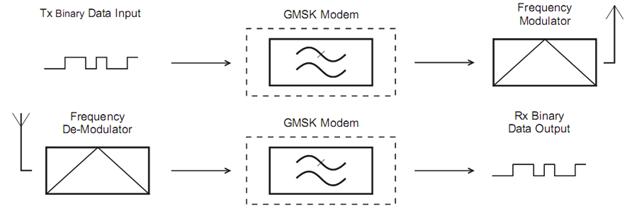
На диаграмме ниже представлены выходы фильтра GMSK для входной логической последовательности “1 0 0 0 1 0 0 0”. Обратите внимание на задержку после фильтра и на то, что отдельный импульс растягивается более чем на один период.
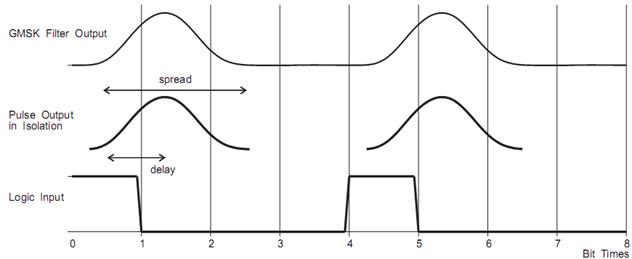
Настоящая GMSK передача, в радио, достигается когда данные с выхода Гауссового фильтра проходят через FM модулятор сохраняющий свойство неразрывности фазы, и у которого пиковая девиация равна половине используемой скорости передачи в битах. Max девиация (Hz) = Скорость передачи данных/2. Например, DEVMAX = 2kHz для скорости 4kbits/sec.
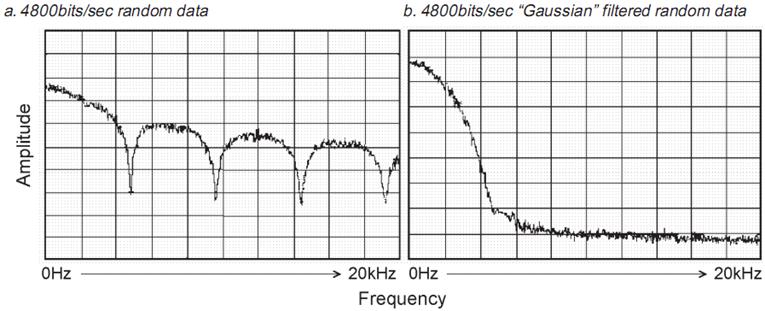
Т.О. Максимальная скорость передачи данных, которая может быть достигнута по радио каналу зависит от следующего –
- Ширина канала
- Допустимая интерференция с соседним каналом
- Полоса фильтра Tx (BT)
- Пиковая девиация несущей (Индекс модуляции)
- Точность установки несущей Tx и Rx
- Линейность модулятора и демодулятора
- Частотные и фазовые характеристики фильтра IF Rx
- Используемые методы коррекции ошибок
- Приемлемый уровень ошибок
В современной теории цифровой связи не существует однозначного инженерного подхода к выбору фильтров в основной (немодулированной) полосе частот [1, 2, 3]. Это вызвано тем, что теория (теорема Найквиста о МСИ-нулевой межсимвольной интерференции) есть только для идеального ФНЧ с прямоугольной характеристикой АЧХ по частоте Найквиста. Однако, этот фильтр не отвечает двум главным требованиям инженерной практики. Они (TX и RX) не являются причинными и физически реализуемыми. Здесь «причинность» понимается, как отклик фильтра после начала воздействия переднего фронта битового импульса. А «физическая реализуемость» понимается, как минимально возможный технически порядок рекурсивного (IIF-БИХ) или не рекурсивного фильтра (FIR-КИХ) при практической создании на реальных элементах радиотехники. С другой стороны теорема Найквиста о минимальной полосе канала связи и теорема Найквиста о частичной симметрии фильтра низких частот с характеристикой приподнятого косинуса дают неполную картину правил построения фильтров канала цифровой связи.
В настоящей работе дается простая и прецизионная методика инженерного решения этих задач с точностью до несущественного множителя. Кроме того, приводится аргументированное теоретически и практически доказательство единственности возможного правильного решения столь сложной совокупности задач связи. Рассмотрим более внимательней это.
Современные представления о нулевой МСИ.
Утверждение 1.
Что нужно для нулевой МСИ? Сигнал может запаздывать и иметь иной масштаб по амплитуде. Следовательно:
yвых(t)=kxвх(t-to), (1)
где:
yвых(t) – выходной сигнал канала связи,
xвх(t) – входной сигнал канала связи,
k- масштаб,
to- запаздывание (или To).
С другой стороны выходной сигнал канала связи y(t) является сверткой входного сигнала x(t) с импульсной характеристикой канала связи h(t).
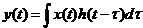 (2)
(2)
Применим к обоим частям формулы (2) преобразование Фурье получим:
y(f)=kx(f)e-i2πfTo (3)
Поскольку свертка во временной области превращается в умножение в частотной области из уравнения (2) получим:
Y(f)=X(f)H(f) (4)
Где:
Y(f) –спектр выходного сигнала,
X(f)-спектр входного сигнала,
H(f)- АЧХ канала связи.
Или
H(f)=Y(f)/X(f) (5)
Подставим уравнение (1) в уравнение (5) видим, что АЧХ канала связи с нулевой МСИ имеет вид:
H(f)=ke -i2πfTo (6)
Из этого уравнения (6) классическая формулировка гласит следующим образом:
» Для нулевой МСИ отклик канала связи (его АЧХ) должен иметь постоянный модуль, а сдвиг фаз должен быть постоянным по частоте…»[3, стр 64].
Утверждение 2.
Следует заметить, что такой вывод (Утв. 1) сделан для канала связи в целом. Сам же канал связи состоит из передающего фильтра и приемного. В [4, стр 109] говориться, что при отсутствии искажений и МСИ, прием сигнала из канала связи после передающего фильтра можно выполнить на согласованный с сигналом фильтр. Причем, передаточная функция которого должна быть комплексно сопряженной со спектром сигнала из канала связи, т.е. с сигналом, прошедшего фильтр передатчика модема.
Утверждение 3.
Терема Найквиста о минимальной полосе канала связи [2, стр138] гласит: Если синхронные короткие импульсы с частотой следования Fsсимволов в секунду подаются в канал, имеющий идеальную прямоугольную АЧХ с частотой среза Fn=1/2Fs Гц, то отклик на эти импульсы можно наблюдать независимо, т.е. без МСИ.
Утверждение 4.
Теорема Найквиста о частичной симметрии фильтра с приподнятым косинусом гласит [2, стр 140]: суммирование действительной кососимметричной функции передачи с характеристикой идеального ФНЧ сохраняет моменты пересечения импульсной характеристики с нулевой осью. Это необходимое условия нулевой МСИ. Свойство симметрии при этом рассматривается относительно частоты Найквиста Fn.
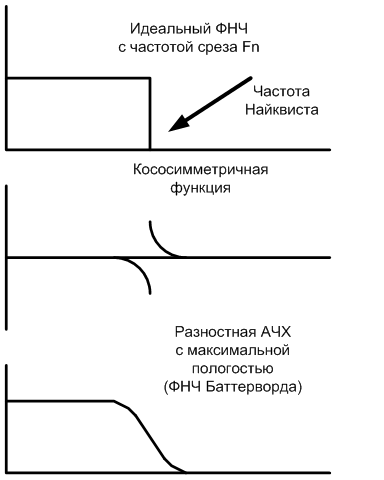
Рис1 Теорема Найквиста о частичной симметрии.
Заметим, что указанная разность дает обычную АЧХ с максимальной пологостью, из всех известных типов фильтров, т.е. АЧХ типового фильтра Баттерворда. А ни какого иного фильтра. Упоминания о фильтре с приподнятым косинусом в первоисточнике нет. Этот фильтр присутствует только в названии теоремы о частичной симметрии.
Кроме того, канал связи (АЧХ или идеальный фильтр) с характеристикой по формуле (6) не реализуем в действительности, т.к. он нарушает принцип причинности и его порядок ставит инженеров тупик при реализации в виде не рекурсивных фильтров из-за ограничений по порядку фильтра. А порядок фильтра от 150 и более требует таких вычислительных ресурсов, что современные DSP/PLIS реализации просто не могут работать из-за больших токов потребления. Проблема в целом становиться неразрешимой. Попробуем в этом разобраться и сформулировать так теоремы о нулевой МСИ, чтобы не нарушать полученных результатов, но иметь качественно новые результаты, позволяющие преодолеть отмеченный набор противоречий.
Графически теоремы Найквиста и её интерпретации разных авторов о межсимвольной интерференции в основной немодулированной полосе частот сводятся к следующему: частота среза фильтра должна быть равна частоте 2Fn (частота Найквиста), групповое время запаздывания фильтра должно быть константой в полосе пропускания, а фаза д.б. линейно нарастающей (убывающей функцией) в полосе пропускания, что и представлено:
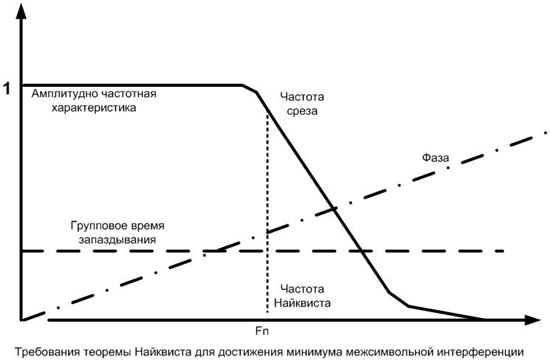
Выводы.
Для анализа противоречий был выполнен анализ известных фильтров применяемых в радиотехнике совместно с кодом NRZ и по поведению BERвыявлены наиболее помехоустойчивые и отвечающие признаку причинности и физической реализуемости. Анализ велся сразу с известным полосовым приемным фильтром Баттерворда. Например, первично для скорости 7400Бит/с был выбран физически реализуемый BPF типа IIR 4-го порядка с полосой 10-3700Гц. Нижняя частота определялась, как реальная минимальная возможная учитывающая наличие переходных конденсаторов в канале связи, а верхняя как частота Найквиста по теоретическим утверждениям. Причем, первично был взят 2-порядок фильтра, как минимально возможный. Не рекурсивные фильтры Banpass были отвергнуты сразу по причине требования высокого порядка (не менее 200) на низких частотах для получения полос пропускания от 10Гц с требуемым наклоном АЧХ.
Перечень исследованных передающих/приемных фильтров (1976-2010г.г.).
FIR-КИХ нерекурсивные фильтры:
- Lowpass
- Gauassin
- Root raiset cosine
- Rasiset cosine
Типа
- Rectangular
- Bartlett
- Blacman
- Hamming
- Hanning
- Kaiser
Всего 24 разновидности.
Результаты по BER не могли быть получены меньшими 10-18dB при вероятности ошибки 10е-5.
Рекурсивные фильтры:
исследованы фильтры Баттерворда, Чебышева, Бесселя и Эллиптические.
Фильтры Баттерворда.
Наилучшие результаты по BER 5.5dB (Pe=10t-5) для основной немодулированной полосы частот получены с фильтрами Баттерворда. Рассмотрим это и на основе полученных данных сформулируем новую трактовку набора теорем о нулевой МСИ для физически реализуемых фильтров для ограниченных по полосе сигналов, не нарушающих принцип причинности, и определим следствия из них.
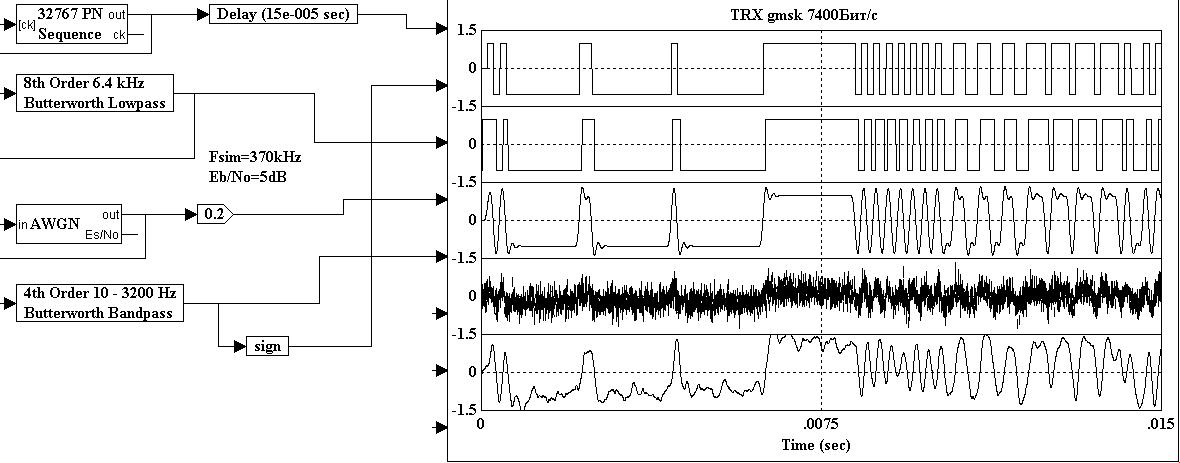
Вид сигналов в канале связи, например, при 7400Бит/с Eв/No=5dB Fsim=180kHz. Демодуляция сигнала происходит при отношении сигнал/шум 5dB. Форма сигнала TX имеет вид апериодического затухающего звена с длинной спада до 3 бит.
Передающий ФНЧ:
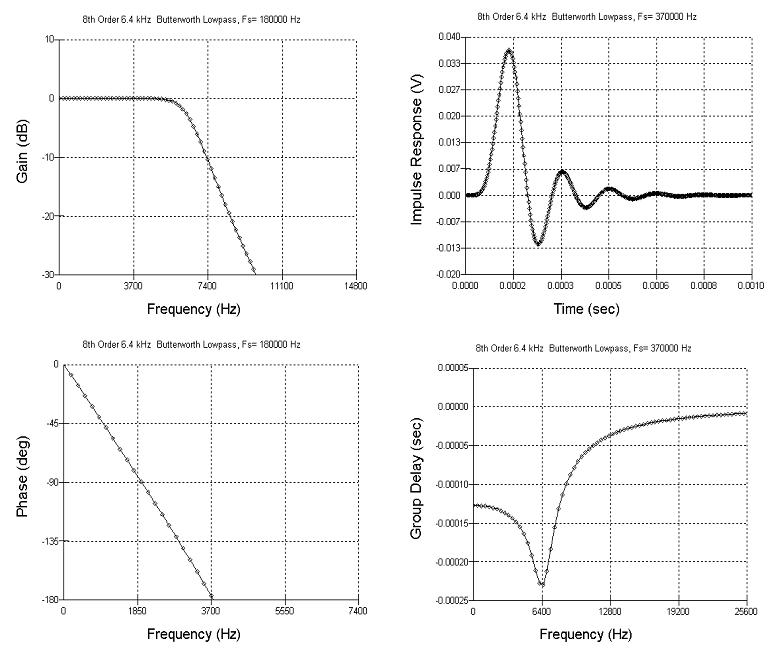
Отклик на единичный бит имеет сдвиг по времени строго на 1 Бит. Амплитуда выброса (перерегулирование) больше примерно в 1.2 раза. Импульсная функция d(t) имеет вид затухающего апериодического звена с длиной отклика 5 Бит. Принцип причинности выполнен полностью. Особая точка на АЧХ фильтра TX (-10dB) на частоте 2Fn. Особая точка ФЧХ – сдвиг на 180 градусов на частоте Fn. Особая точка – максимум запаздывания 23мс для скорости цифрового потока 3700Бит/с на частоте 6400Гц . Что составляет 1.72Fn.
Приемный фильтр ФНЧ
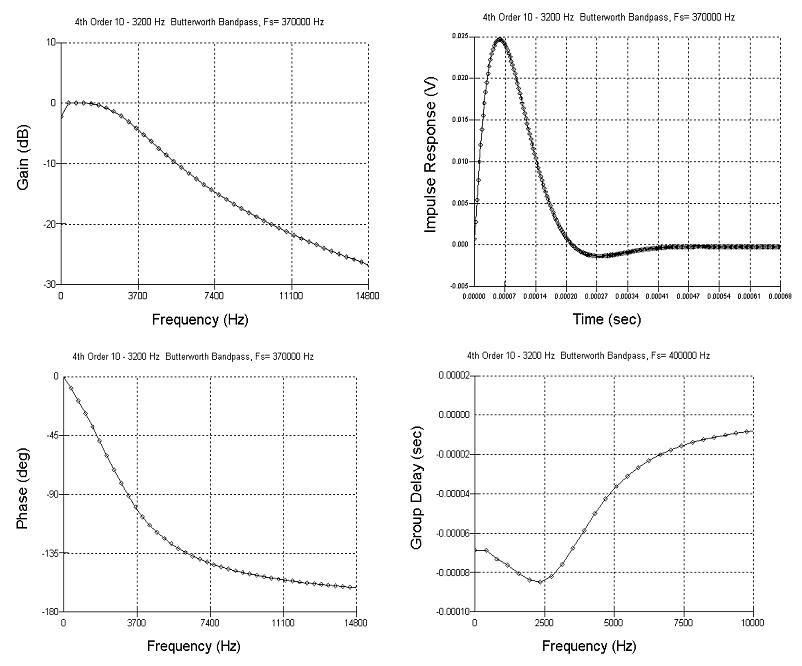
Длительность отклика по нулевому уровню равна 27.02мс, что точно соответствует длине бита. Протяженность отклика 3.5 бита. Принцип причинности не нарушен. Особая точка -10dB на частоте 5550Гц равная 1.5Fn. Особые точки 3600Гц сдвиг фазы 90 градусов и 7400Гц сдвиг фазы 150 градусов. Все частоты после 2Fn имеют сдвиг по фазе 180градусов. Особая точка – максимум задержки 8.5мс на частоте 2400Гц, что равно 0.64Fn
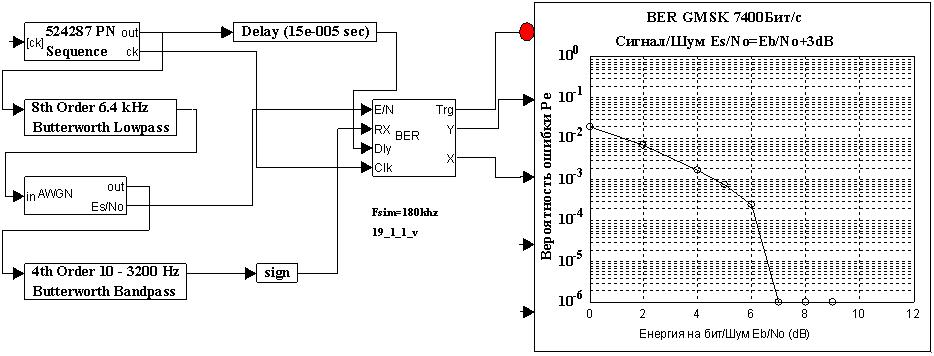
BER канала связи на скорости 7400Бит/с. При 10е-5 Eb/No=6.5dB. Метод требует рекуренты из 19 триггеров. Наиболее часто используемые рекуренты на 17 и 23 триггера в скремблерах дают помехоустойчивость не меннее 9-10dB. Это нужно учесть.
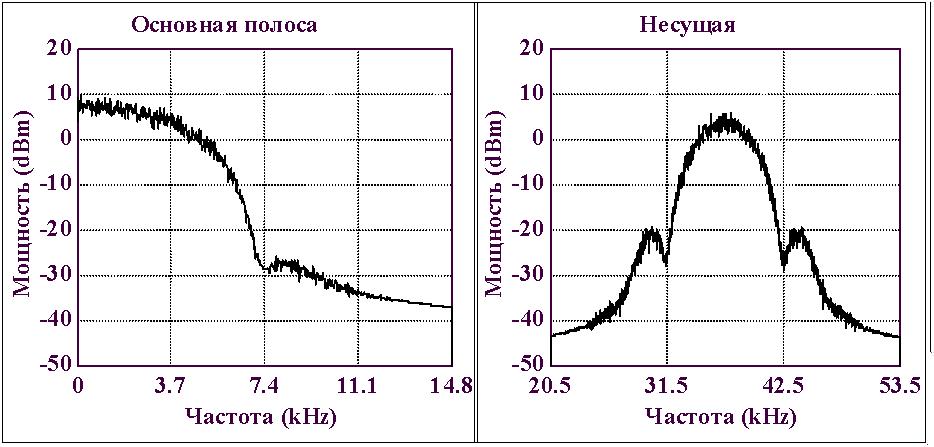
Спектры в основной полосе и на несущей. Ширина спектра на несущей по уровню -20dBm равна 10кГц.
Углубленный анализ
Для углубленного анализа применим разные процедуры измерений во временной и спектральной области. Задача этих измерений получить признаки особого поведения вблизи частоты Найквиста и ее удвоенного значения, а так же на длине одного и двух битов во времени. Совместим спектры фильтров TX и RX на один измеритель и подадим два вида испытательных сигналов – рекурента на базе 19 триггеров и белый шум.
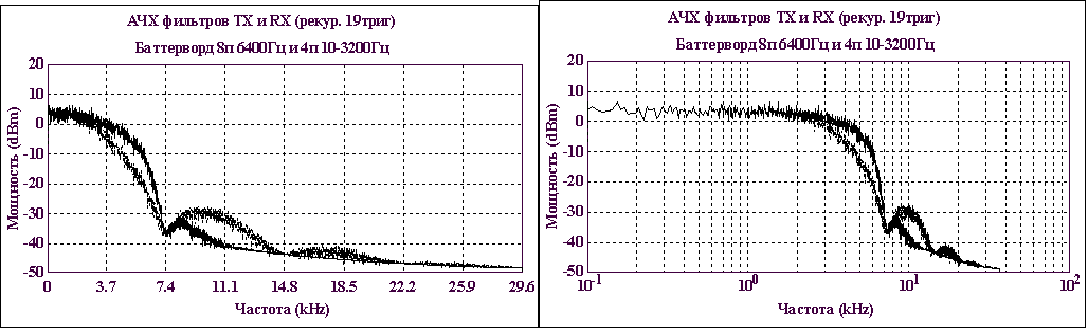
Линейные и логарифмические спектры фильтров TX и RX при входной рекуренте из 19 триггеров на скорости 7400Бит/с. По этим спектрам ничего необычного обнаружить нельзя. Для получения новой измерительной информации (!) подадим на оба фильтра аналоговый белый шум и совместим выходные спектры на один измеритель.
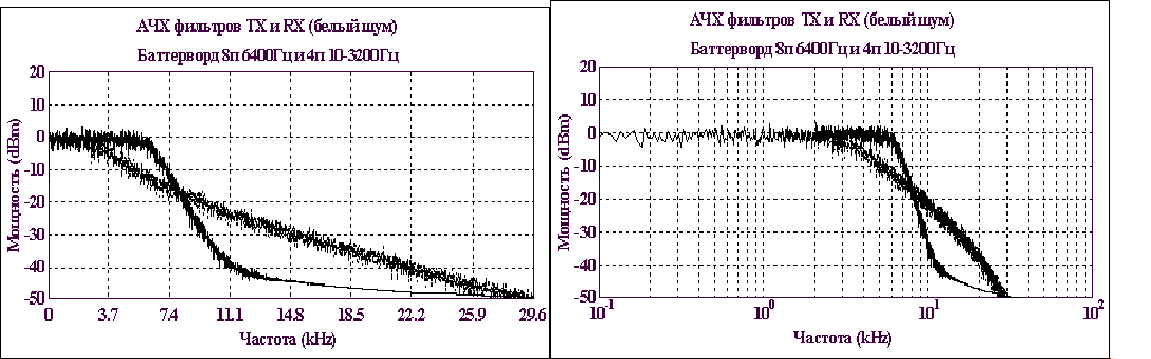
Линейный и логарифмический спектры фильтров TX/RX при испытании аналоговым белым шумом. Особая точка пересечения и частичной симметрии находиться вблизи 2Fn, а не на частоте Найквиста Fn . На уровне -17dBm. Явно видна синусоидальная частичная симметрия АЧХ фильтра TX 8-го порядка относительно фильтра RX 4-го порядка, как плавающей оси абсцисс. Это очень важный новый научный признак. Тем более что испытания фильтров белым шумом более полные и правильные и имеют совсем иные физические принципы. Повторить эти измерения может любой исследователь легко в любой оболочке типа MatLab, LabView, SystemView, CommSim и т.п.
Использование разностного спектра.
Усложним метод получения новой научной информации. Для этого измерим разностные спектры фильтров TX/RX при одновременном подключении к одному источнику сигнала, например рекуренте из 19 триггеров. Причем в двух вариантах, последовательно, как они стоят реально в канале связи связи и параллельно. Это нужно для выявления инвариантности разностного спектра строго отвечающего за наличие МСИ. Просто потому, что противофазные компоненты разностного спектра передающего и приемного фильтров при отсутсвии межсимвольной интерференции обязаны быть подавлены. В этом измерительном опыте глубочайшая фундаментальная суть новых предствлений о МСИ! Только мера разностного спектра может служить реальной инженерной оценкой МСИ. Все остальные известные в мире связи методики лишь приближенные эмпирические оценки. В реальном канале связи передающий и приемный фильтр включены последовательно, но мы будем проверять и их параллельное включение. Это нужно для обоснования иных каналов связи в дальнейшем.
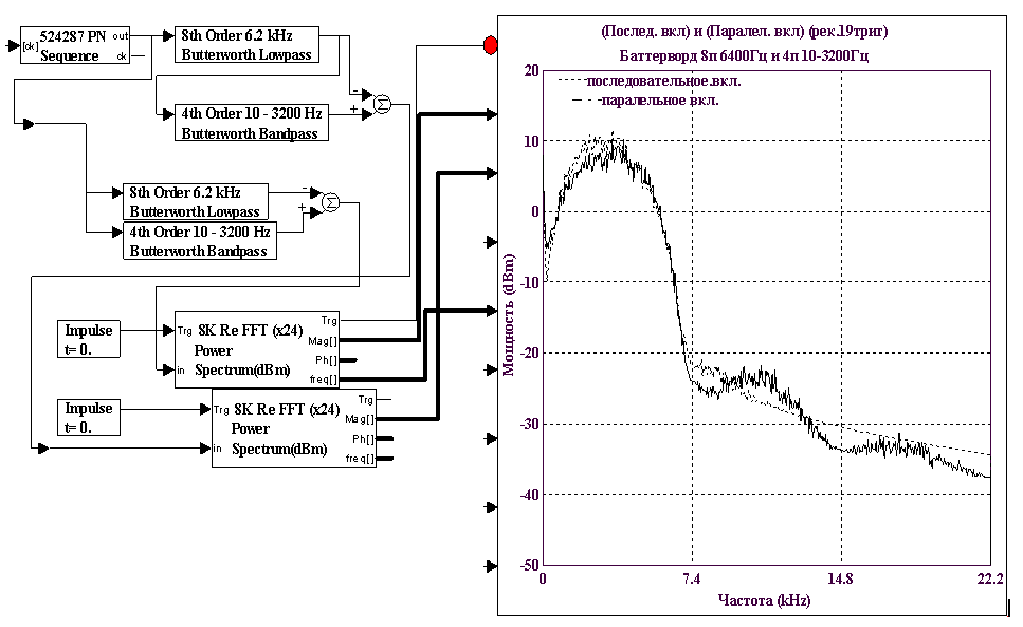
Спектры разности фильтров TX/RX при последовательном и параллельном подключении к одному источнику сигнала «рекурента из 19триггеров». Особая точка – частота 7400Гц (2Fn). Все частоты выше 2Fn подавлены на 35dBm. Причем тип включения параллельно/последовательно дает существенные отличия синусоидального характера только после 2Fn. Но принципиальных отличий нет. Оба типа включения дают почти подобные функции в общем характере поведения. Физический смысл исследуемых разностных спектров – это фактически спектр импульсной характеристики канала связи в целом. Он дает информацию о значительном подавлении МСИ (-35dBm) на частотах выше 2Fn.
Теперь то же самое, но от источника белого шума.
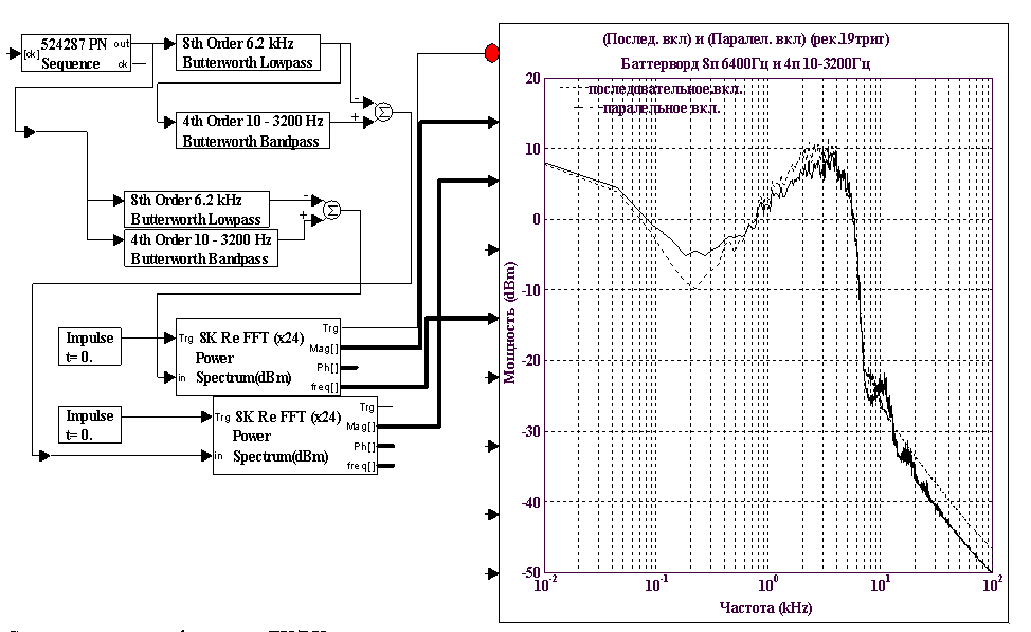
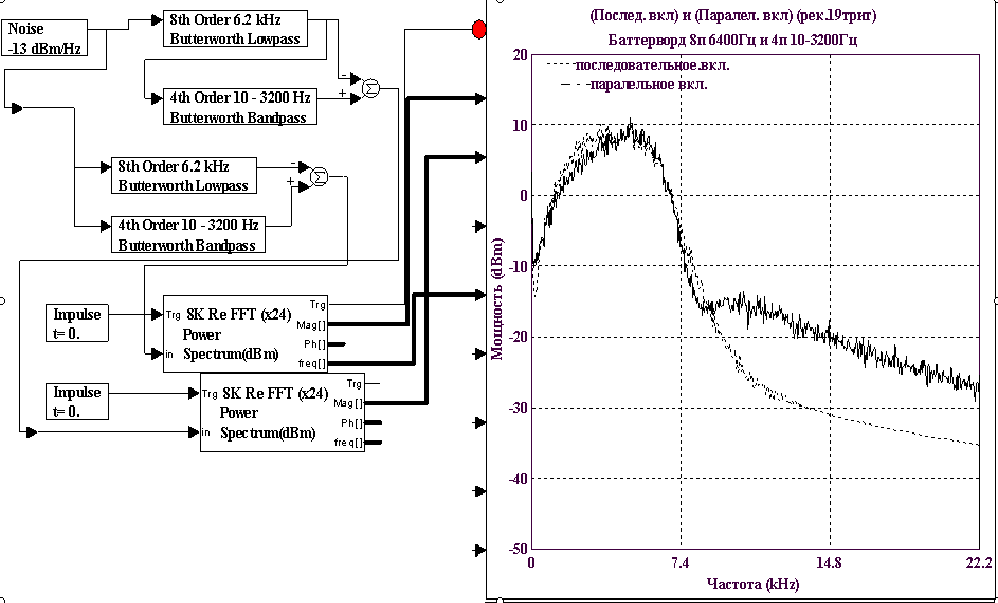
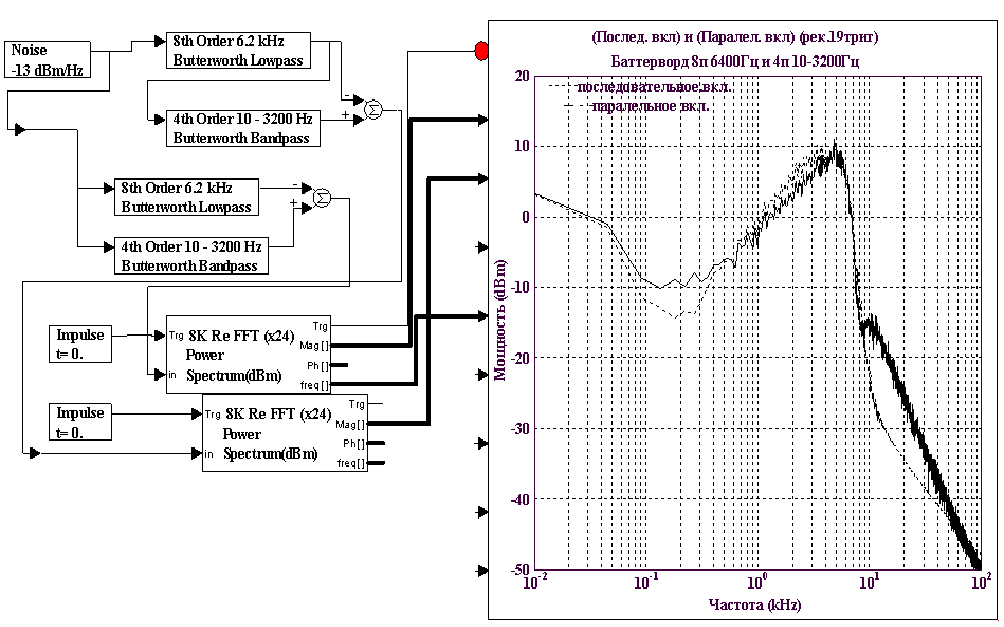
Разностные спектры фильтров TX/RX при испытательном сигнале «белый шум». Общий вид подавления МСИ сохранился, но из-за рассогласования их АЧХ со спектром испытательного сигнала подавлении вблизи 2Fn хуже. Усложним далее методику получения измерительной информации. Теперь подадим на входы при последовательном включении и параллельном разные сигналы цифровую рекуренту из 19 триггеров на скорости 7400Бит/с и аналоговый белый шум и совместим спектры.
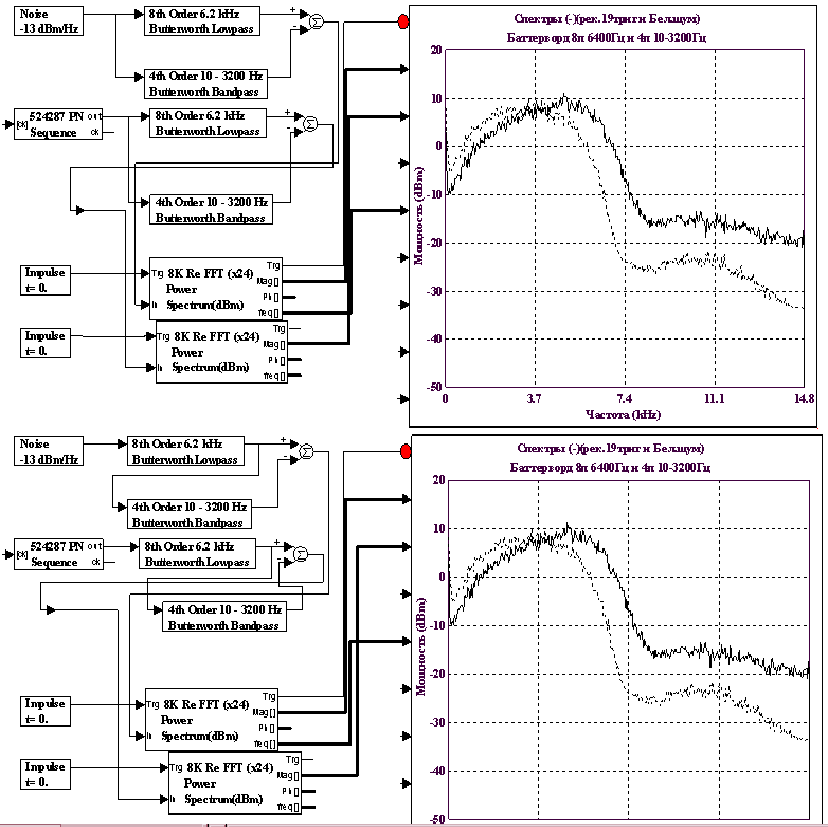
Разностные спектры фильтров TX/RX при разных испытательных сигналах и последовательном/параллельном включении. Явно видна инвариантность положения точки пересечения (частичной симметрии) относительно уже известной особой точки «частоты Найквиста» при последовательном или параллельном включении. Это очень хорошее свойство АЧХ найденных фильтров. На его базе будет ниже сформулирована новая теорема об инвариантности частоты Найквиста.
Анализ во временной области.
Перейдем к анализу во временной области. Для этого сформируем наблюдение выходных сигналов самих фильтров и их разности при действии особого испытательного сигнала. Этот сигнал должен одновременно показать отклики фильтров на единичный бит, ступеньку и устойчивость канала связи к пропуску длинных серий единиц и нулей. Последнее свойство крайне важно для проектирования и обоснованного отказа от скремблеров или потоковой свертки через задержку, неизбежных при построении каналов связи по теоремам Найквиста. Размножение ошибок и потери на синхронизацию основные факторы потерь на 6dB по BER. Очень заманчиво, убрать скремблер или потоковую свертку для того, чтобы операции перемежения и сверточного кодирования, дающие 6-10dB по BER работали для иных целей. Т.е для борьбы с внешними помехами по эфиру, а не для компенсации потерь от скремблера (синхронизация) или потоковой свертки (размножение ошибок).
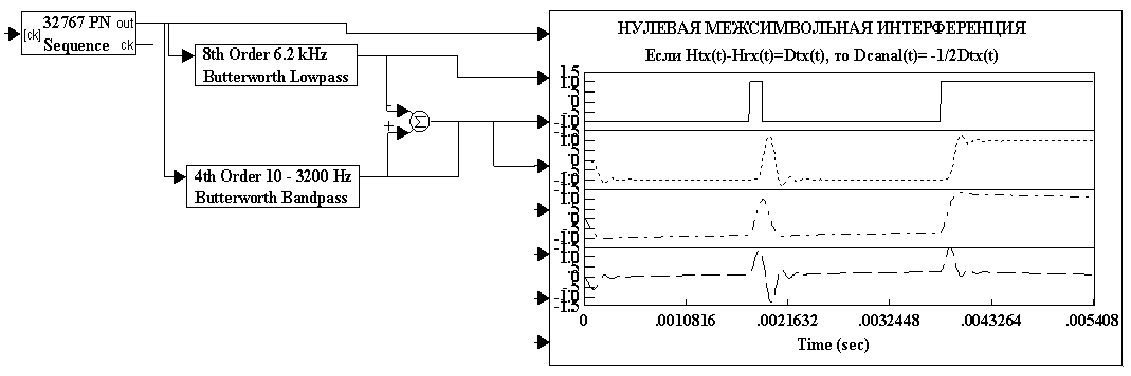
Выходные сигналы фильтров и их разность при действии рекуренты из 15 триггеров с участками серий 14 нолей, 14 единиц, одиночного бита и ступеньки. 1 график испытательной рекуренты, 2- выход TX, 3- выход RX, 4-разность. На графке видно наличие переходных конденсаторов в канале связи по постепенному изменению постоянных составляющих на участках серий нолей и единиц по 14 штук. Это влияние теперь ни как не сказывается на возможности декодирования потому, что фильтры подобраны верно. В канале можно оставлять теперь только процедуру Бит-стаффинга. Т.е применять специальный кодер/декодер на цифровом потоке не позволяющий одновременно передавать, например, больше 6 единиц или нолей. Почему 6 бит? Потому, что флаг в пакетных протоколах любого типа представлен кодом 01111110 или 10000001. Запас по декодированию серий из 14 бит одного логического состояния битового потока полностью и навсегда закрывает этот вопрос. Выбранный тип испытательного сигнала подобран таким образом, чтобы было непосредственно видно переходные и импульсные характеристики фильтров при последовательном и параллельном включении. Из анализа сигналов можно сформулировать основную теорему о нулевой МСИ для фильтров Баттерворда.
новые теоремы
«о нулевой межсимвольной интерференцией в каналах связи с ограниченным спектром»
Теорема 1.
«О равенстве общей импульсной характеристики канала связи и импульсной характеристики передающего фильтра Баттерворда при нулевой МСИ для сигналов с ограниченным спектром.»
Если разность переходной характеристики передающего ФНЧ Баттерворда 8 порядка и приемного ПФ Баттерворда 4 порядка равна импульсной характеристике передающего ФНЧ, то общая импульсная характеристика канала связи равна минус 1/2передающего ФНЧ. При этом частота среза передающего ФНЧ должна быть равна 0.86*2Fn, а верхняя частота среза приемного ПФ должна быть равна 0.86Fn. Нижняя частота среза определяется минимально возможной частотой из реальных номиналов неизбежных переходных конденсаторов в канале связи.
Т.О.
Новые инженерные формулы для минимума межсимвольной интерференции для каналов связи с ограниченным спектром таковы:
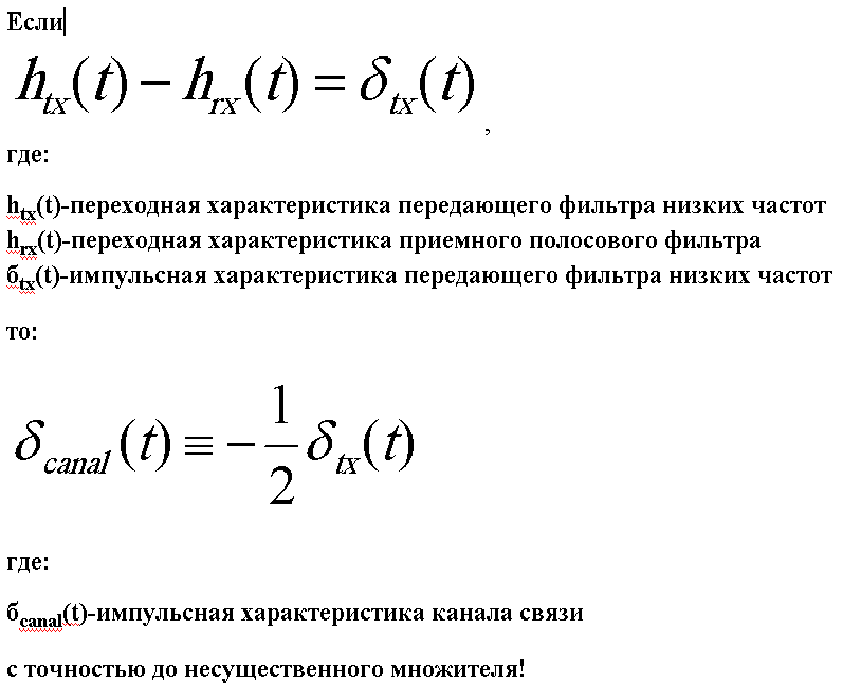
Наглядно (графически) доказывается это так:

Замечание. Импульсная характеристика передающего фильтра равна импульсной характеристике всего канал связи. Это очень серьезное заявление, с такими последствиями, что трудно даже интерпретировать, что это означает физически. Ниже показана первая в мире Автоматизированная система управления каналом связи по выше изложенным формулам. Красный график это временной отклик передающего фильтра, зеленый приемного. Как видно на нижнем правом рисунке, отклики передающего и приемного фильтров на одиночный бит полностью совпали при установке нужной задержки и масштабного коэффициента. Синий разностный отклик практически показывает нулевую интерференцию. Выбирая частоты среза передающего и приемного фильтра по минимуму разности можно построить АСУ любого кнала связи при действии любого вида помех. На приемной стороне не требуется знания отклика передающего фильтра, вместо него может работать его эталонная модель. Причем, разность всегда при отклонении от минимума меняет полярность, что позволяет строить однозначные системы АСУ.
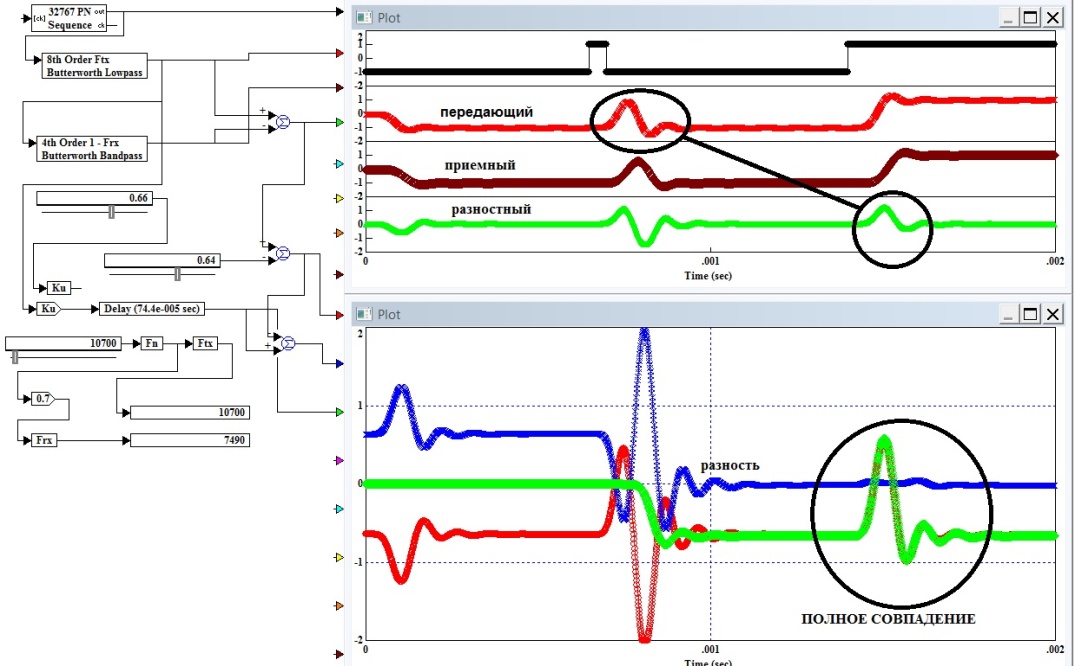
Спектры при испытаниях белым шумом:
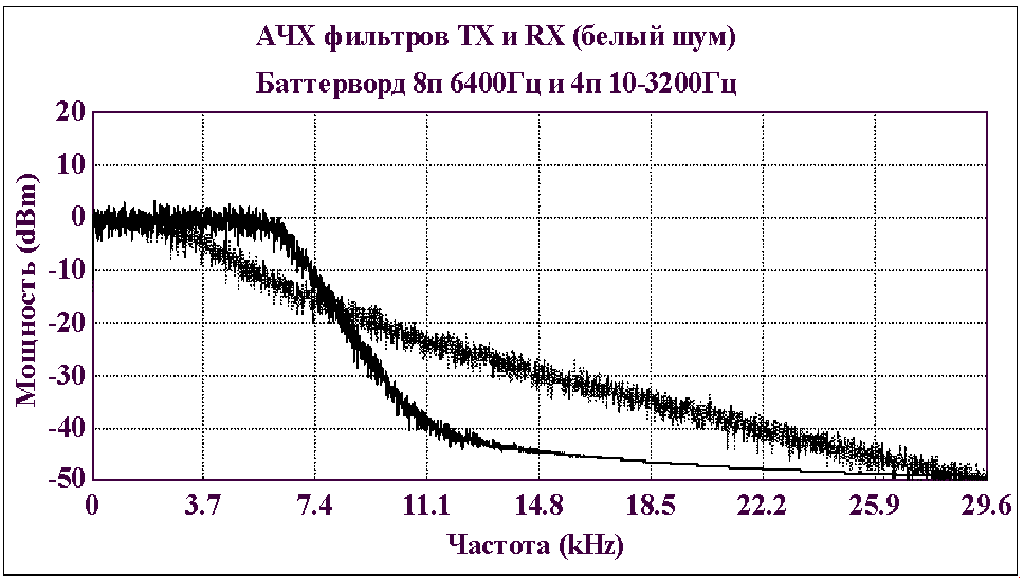
Где: где Fn-частота Найквиста. (скорость7400bps)
Найквист говорит: частота среза фильтра должна быть равна частоте Fn (частота Найквиста), групповое время запаздывания фильтра должно быть константой в полосе пропускания, а фаза д.б. линейно нарастающей (убывающей функцией) в полосе пропускания.
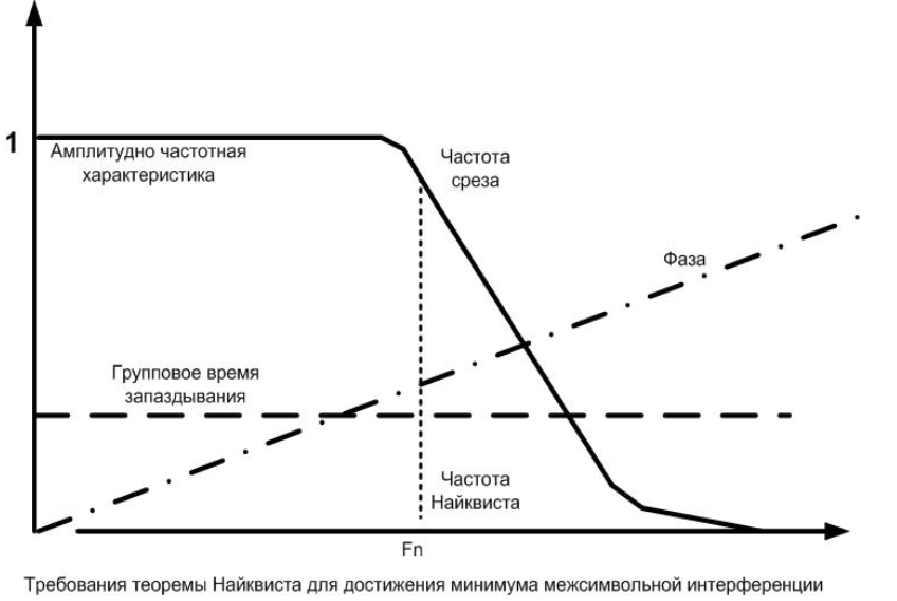
В свою очередь требования новых теорем принципиально иные. Они таковы:
частота среза фильтра «равна» частоте Найквиста (по теореме 1, отдельно для фильтров TX и RX), но фаза должна быть равна нулюна частоте среза Fs=Fn, а групповое время запаздывания должно иметь максимум на частоте среза Fs. Плюс 5 теорем упомянутых выше и фундаментальная инженерная формула о равенстве разности переходных характеристик фильтров TX и RX импульсной характеристике фильтра TX.
Ниже показан пример характеристик TX фильтра (АЧХ, ФЧХ и ГВЗ) для скорости 9600bps по теоремам о МСИ Батухтина.
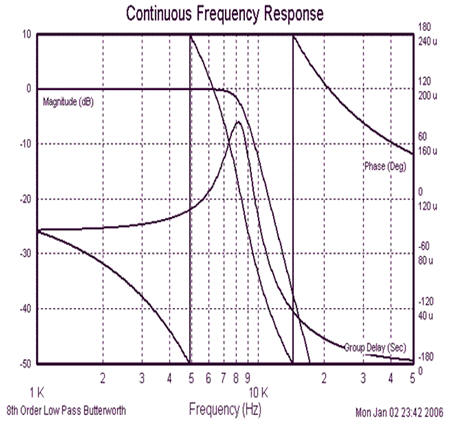
инженерное Доказательство единственности решения новых теорем о МСИ.
Докажем теперь, что Теорема 1 является единственным возможным решением не нарушающим принципы физической реализуемости и причинности. Для этого проверим известные фильтры рекомендуемые теоремами Найквиста к применению на наличие подавления спектра выше 2Fn в разностном спектре фильтров TX и RX по следующей схеме:
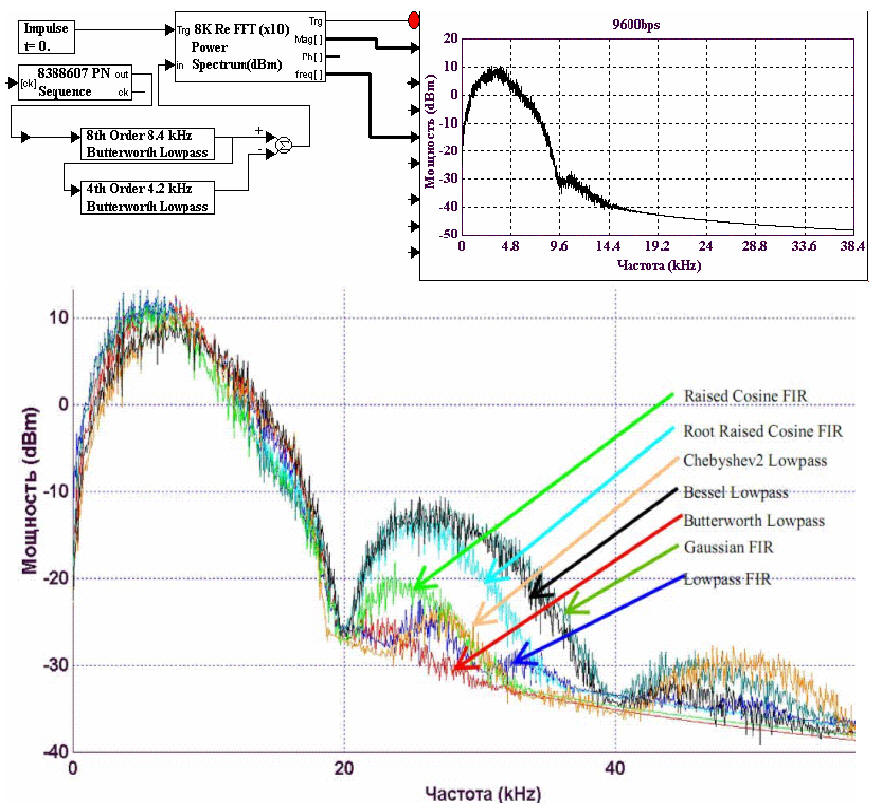
Итоговое доказательство ошибки Найквиста для большинства известных типов фильтров выразилось в том, что все известные фильтры, кроме Баттерворда имеют выше 2Fn в разностном спектре TX-RX сигнала не скомпенсированные противофазные гармоники, собственно межсимвольную интерференцию.
На основании проведенного доказательства сформулируем:
Теорема 2
«О единственности возможного решения нулевой МСИ для сигналов с ограниченным спектром:
Фильтры Баттерворда являются единственно возможным решением нулевой МСИ с характеристиками выбранными по теореме 1 и обладают максимально возможной пологостью при отсутствии нарушения принципа причинности и физизической реализуемости.
Теорема 3.
«О подавлении разностного спектра выше удвоенной частоты Найквиста»
Для достижения нулевой МСИ выбор фильтров необходимо осуществлять таким образом. Чтобы разностный спектр при испытаниях рекурентой или белым шумом передающего и приемного фильтра был подавлен на частотах выше 2Fn не менее 35dBm.
Теорема 4.
«Об измерении нулевой МСИ»
Разностный спектр передающего и приемного фильтров для сигналов с ограниченной полосой является основным измерительным инструментом нулевой МСИ однозначно показывающим нарушение принципа причинности и физической реализуемости.
Теорема 5.
«Об инвариантности измерений нулевой МСИ относительно рекуренты и белого шума»
Разностный спектр фильтров TX/RX инвариантен при испытаниях рекурентой и белым шумом относительно частоты Найквиста.
Для справки дается сводная таблица занимаемой полосы частот и достигнутой помехоустойчивости по теоремам Найквиста современных методов манипуляции и модуляции без использования методов борьбы с групповыми ошибками (перемежение) и одиночными (турбо-сверточные линейные кодеки) в основной немодулированной полосе частот:
МОДЕМ_______BER(10e-5)__Полоса (Hz)
GMSK_________13_________B/2
FSK___________13_________В
PSK___________10_________B
4FSK__________23_________B/2
4PSK__________13_________В/2
8PSK__________18_________B/3
16QAM________20_________B/4
64QAM________26_________B/6
256QAM_______32_________B/8
B-скорость битового потока Бит/с (bps)
Векторные диаграммы имеют красивый вид, что характеризует применение фильтров Гауса.
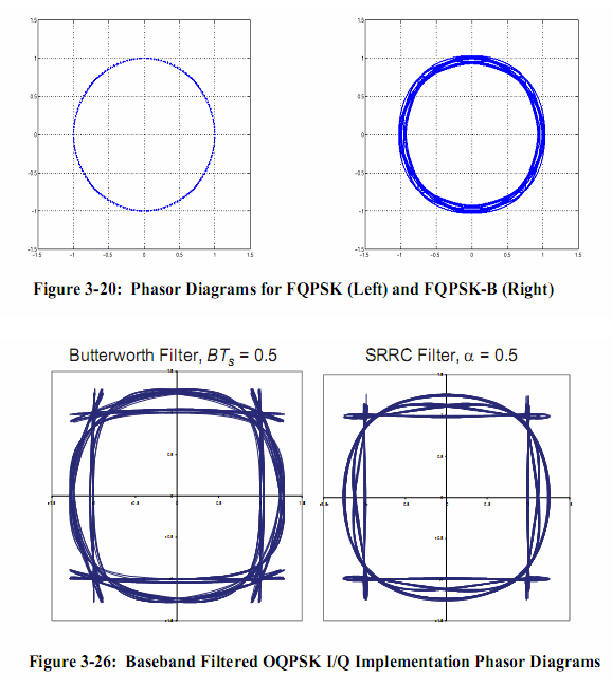
При использовании фильтров Баттерворда не применяются порядки выше 6-го и коэффицент сглаживание равный единице. Влияние постоянной составляющей (переходные конденсаторы) также не читывается.
При этом, во всех работах утверждается, что ниже 2.5dB это предел достигаемой сегодня по теоремам Найквиста о МСИ помехоустойчивости при использовании перемежения и турбосверточных кодеков.
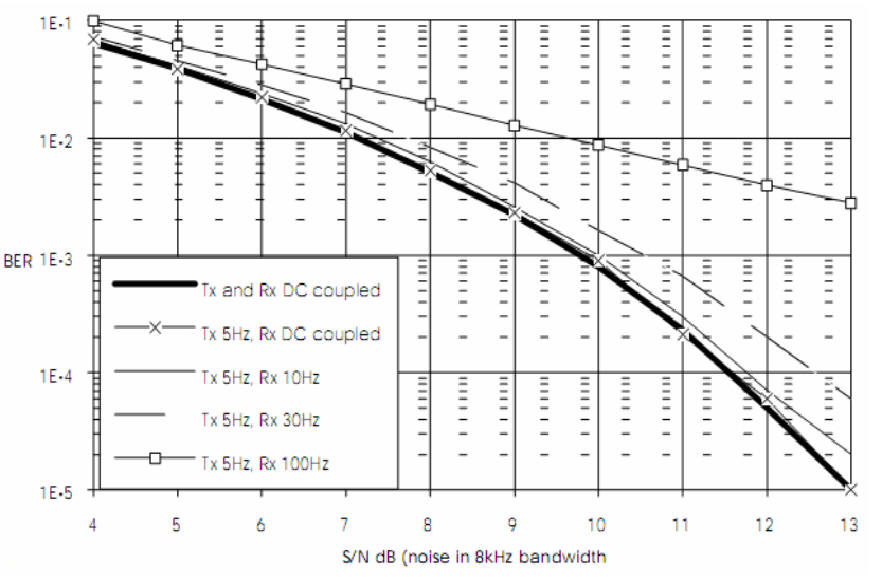
Сравним теперь типовые методы модуляции FM по двум методам формирования, на основе ГУН и по квадратурной схеме, как в сотовых телефонах при правильно подобранных фильтрах по новым теоремам о МСИ.
Практика применения новых теорем о Межсимвольной интерференции
Временной анализ системы FM-GMSK по квадратурной схеме дал следующий вид.
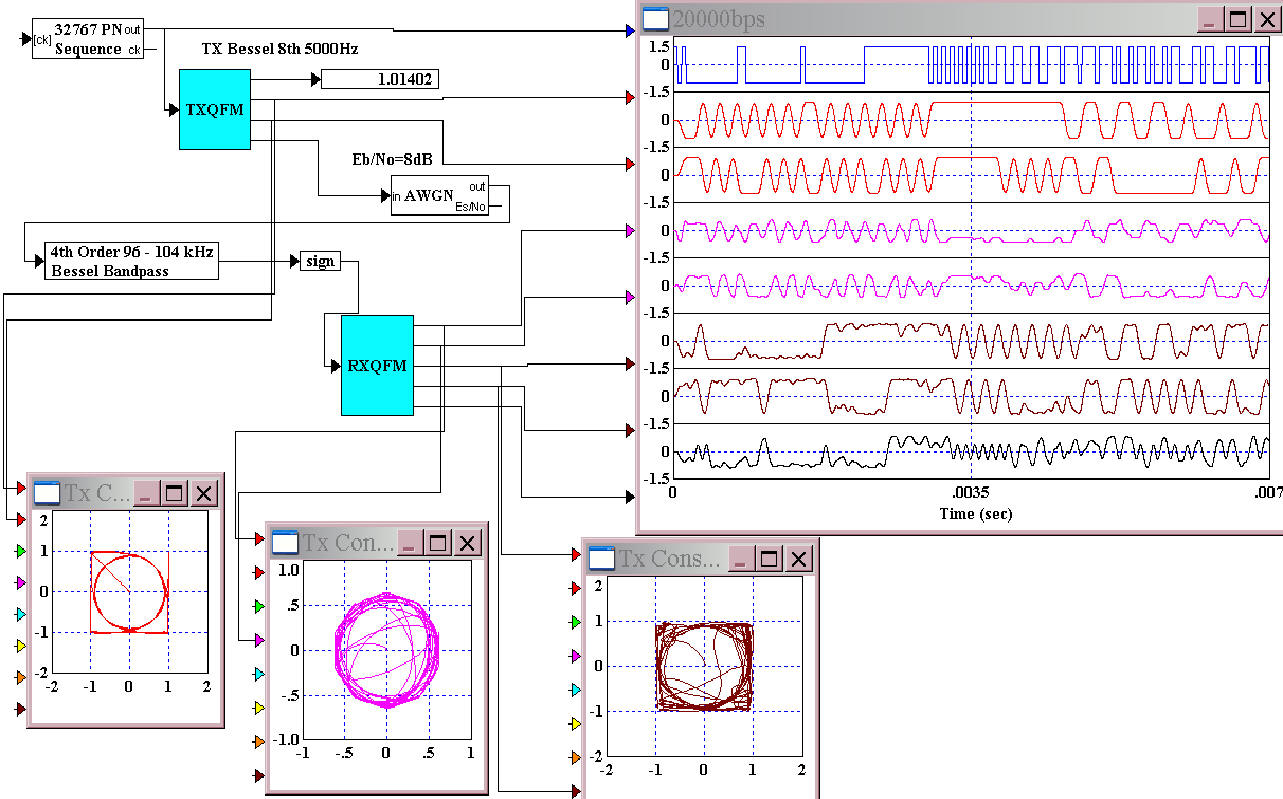
При этом спектры квадратурного метода по сравнению с методом ГУНа заметно изменились. А это вся сотовая телефония планеты!
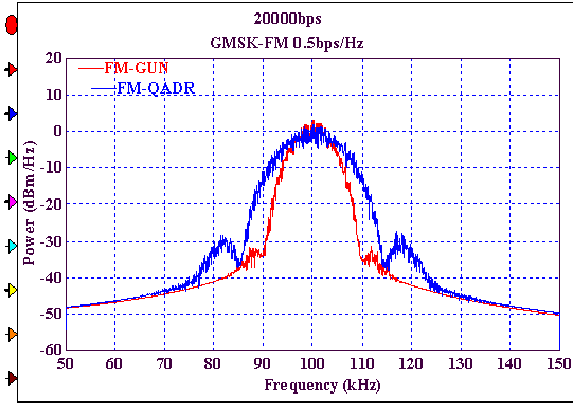
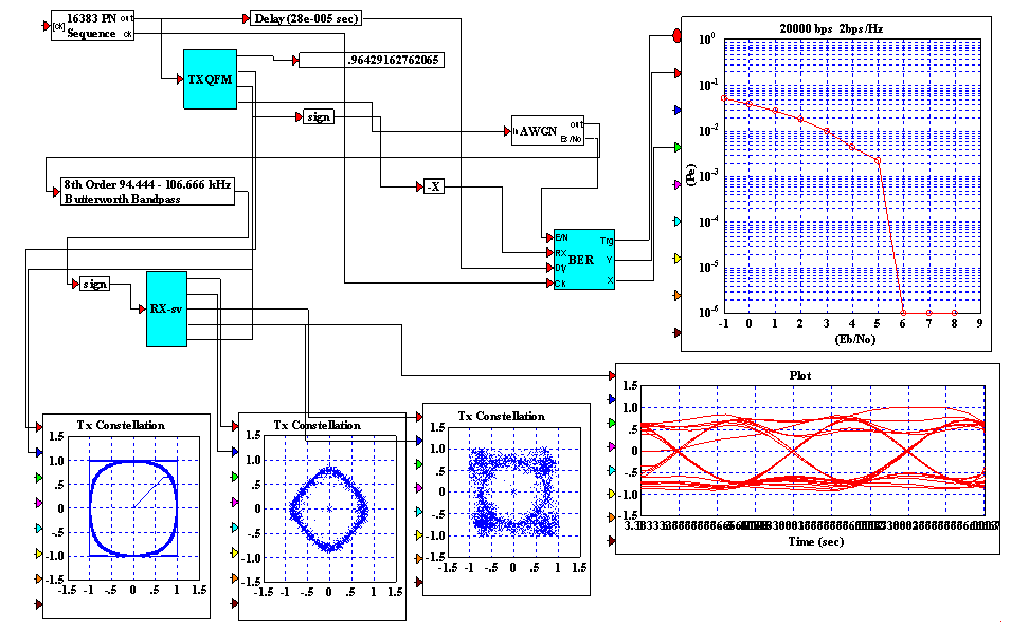
Помехоустойчивость возросла со стандартных 13dB до 5.5 dB почти в 2 раза.
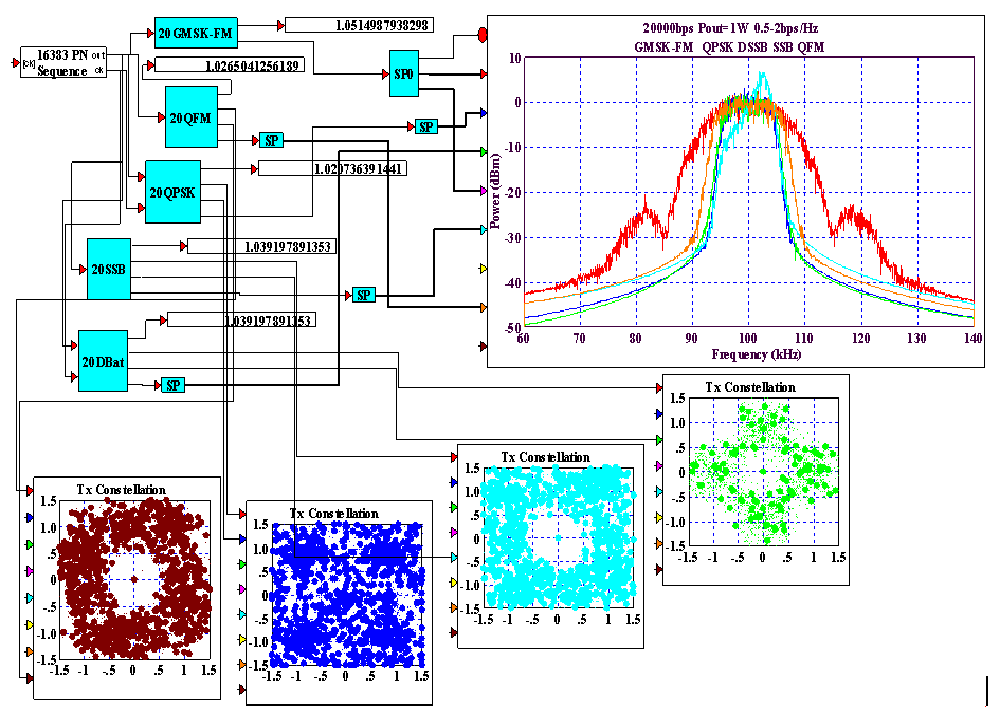
С фильтрами Баттерворда нет вообще привычных для анализа векторных »красивых» диаграмм. А форма спектров приняла почти прямоугольный характер на несущей частоте, как в 1024 OFDM модуляции.
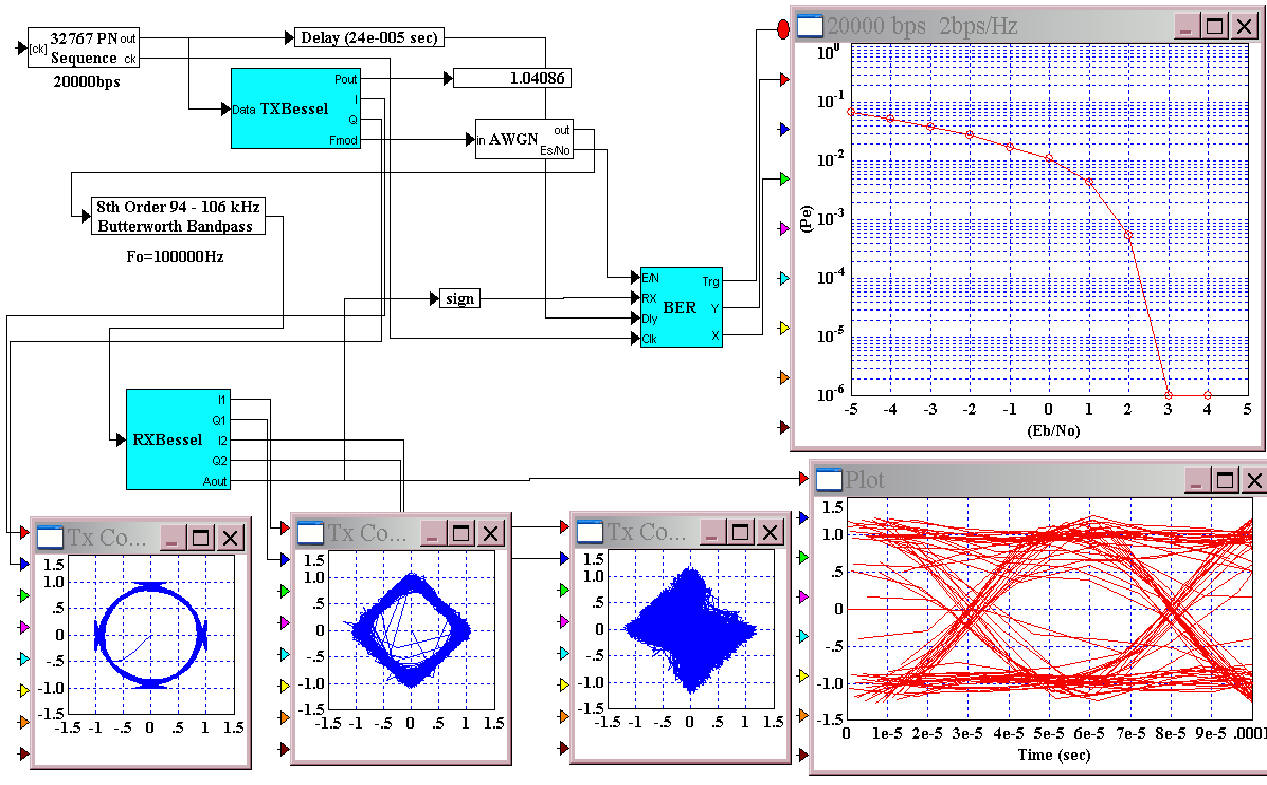
А помехоустойчивость при спектральной эффективности 2bps/Hz достигла таких величин, которые получают в современной цифровой связи для самых сложных схем борьбы с ошибками с применением перемежения и турбо сверточных кодеков (не более 2.5dB на 10е-5). Хотя при разработке они не применялись. Следовательно запас на минус 6dB, что обычно дает применение перемежения и турбо сверточных кодеков еще не использован. Это дает основания полагать, что у связистов планеты Земля может вскоре возникнуть реализации каналов связи с ограниченным спектром с помехоустойчивостью Eb/No=(минус) 4dB при вероятности ошибки Pe=10e-5 со спектральной эффективностью 2-4bps/Hz!
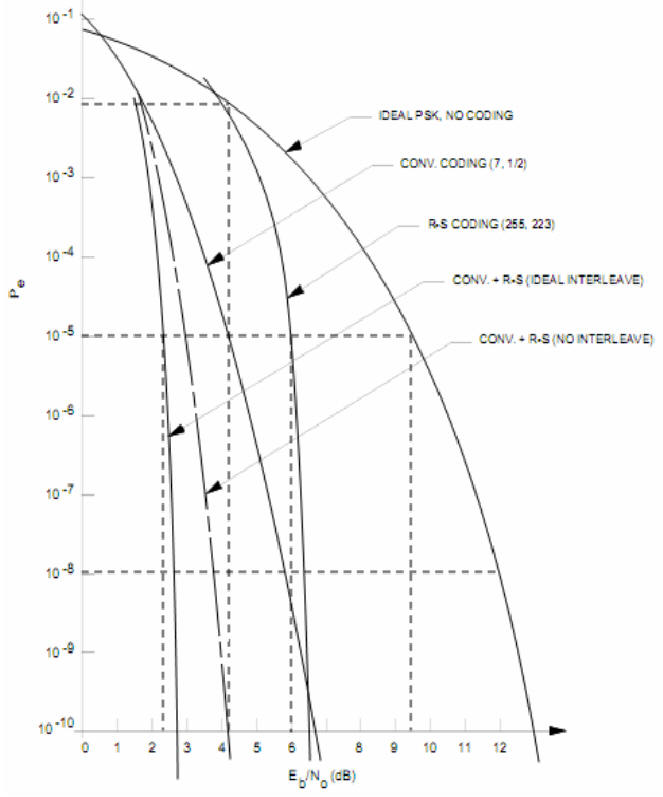
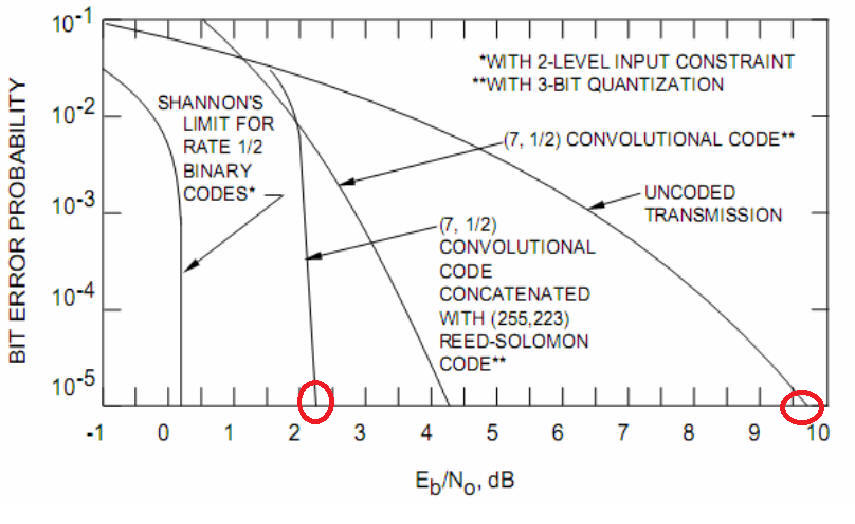
Для глубокого инженерного понимания сказанного выше особое фундаментальное внимание необходимо обратить на тривиальное (!) совпадение номиналов нормированных шкал отношения энергии бита к энергии шума в полосе пропускания Eb/No и соответствующих прямого совпадения значений чувствительности приемника выраженные в микровольтах или dBm для режима 1 Ом, 1 вольт, 1 ампер, 1 ватт!!!! Когда проектант получает график BER=Eb/No нужно всегда его хотя бы «мысленно» достраивать шкалами в микровольтах и в (-dBm). Только в этом случае хорошо наблюдается физика процесса межсимвольной интерференции. На рисунке ниже показаны свойства продукции всех производителей каналов связи планеты на 2010 год по теоремам о МСИ Найквиста.
Все они предлагают продукцию (правый красный кружок) с отношением сигнал/шум (Eb/No) не ниже 8-10 dB при зачетной вероятности ошибкиPe=10e-5 без использования перемежения и турбосверточных кодеков. Это одна ошибка на 100000 бит в потоке данных. Но можно иметь на 6-10dB лучшую помехоустойчивость (левый кружок) сразу, еще не использовав перемежение и турбосветку. Теперь можно начинать проект с отношения сигнал/шум 2.5dB без использования турбосверточных кодеков и перемежения, где все производители проводных и беспроводных модемов заканчивают свою работу с применением турбосверточных кодеков и перемежения. Если же ваша продукция будет иметь встроенные цифровые методы борьбы с одиночными и групповыми ошибками (тубосверточные кодеки и перемежение), то максимальный выигрыш по помехоустойчивости будет меньше еще на 6dB. Таких систем связи в мире просто не существуют ни у кого, но методика дана и нужно её использовать. Пока ни один связист мира не побывал левее 2.5dB для узкополосных каналов связи с ограниченным спекторм из-за ошибки Найквиста в 1928 году. И это основное препятствие для России чтобы иметь геомонополию «по умолчанию» на радиовидимость низких орбит в высокоширотной низкоорбитальной информационной решетке наноспутников ретрансляторов наземных сигналов массовой беспроводной связи (типа сотового) сетецентрической системы
Основными конкурентами на рынке низкоорбитальной связи являются глобальные системы низкоорбитальной спутниковой связи IRIDIUM,GlobalStar, OrbiCom и ГОНЕЦ. Эти системы работают на орбите более 15 лет и имеют не более 100-300 тысяч абонентов:
| № | Компания | Доходы (млн.долл)/число подписчиков (тыс.) | Число КА в ОГ | ||||
| запущено | В работе | ||||||
| ИРИДИУМ | 212/175 | 260/207 | 320/305 | 318/359 | |||
| ГЛОБАЛСТАР | 136/263 | 98/284 | 86/344 | 64/390 | <20 | ||
| ОРБИКОМ | 3/304 | 28/351 | 30/460 | 27/515 | <30 | ||
| ГОНЕЦ | 2/1 | 2/1 | 1/0.5 | 1/0.1 | |||
| ∑ | Итого за всеLeoSAT | 373/743 | 387/843 | 437/1109 | 410/1264 | ||
| … | ИМАРСАТ GeoSAT | 500/228 | 576/233 | 996/245 | 1038/256 |
Основной вывод проведенного анализа наиболее известных низкоорбитальных систем спутниковой связи конкурентов заключается вконстатации следующего неопровержимого факта (!): лишенные многих недостатков геостационарных систем низкоорбитальные системы подвижной спутниковой связи по всем статьям проиграли сражения за потребителя геостационарным системам мобильной связи. Из таблицы следует, что за 4 последних года объем доходов компании геостационарной связи Inmarsat PLS вырос более чем в 2 раза с $500,1 млн до $1038,1 млн, в то время как совокупные доходы всех компаний, эксплуатирующих низкоорбитальную связь, выросли менее чем на 10%: с $373,6 млн до $410,8 млн. Доходы одной компании Inmarsat геостационарной спутниковой связи в 2009 г. в 2,5 раза превысили совокупный доход компаний всех систем низкоорбитальной связи. В этой связи перспектив победного шествия низкоорбитальных систем связи на имеющихся принципах технической реализации и запуска в обозримом будущем не видно, несмотря на то что на их создание потрачено более $20 млрд, Это почти на порядок превышает двадцатилетние затраты на развертывание системы геостационарной спутниковой связи Inmarsat.
Основные причины неудач конкурентов относительно проекта «Система низкоорбитальной связи «КоролСАТ» из столицы Космоса города наукограда Королёва с улицы Гагарина 42 из ГОУ ВПО МО «КИУЭС» такие:
-неправильно выбраны орбиты, а потому и мала абонентская база. Нет угла наклона орбит 65 градусов к плоскости экватора по иконам Православия 12-го века для обеспечения геомонополии на радиовидимость низких орбит. Кстати, южное полушарие низкоорбитального трафика платного глобального почти не дает (не более 10%) при этом.
-нет реальных радиоканалов на дистанции до 2000км работающих с антеннами с усилением не более 3dB, как на передачу, так и на прием. А потому оборудование для связи имеет специальное нестандартное назначение и дорого. Следовательно, нет возможности использовать для работы со спутником привычные массовые средства наземной беспроводной связи, например, типа «Сотовый телефон». В Столице Космоса могут «случайно» быть очень нужные для планеты решения от Разумного Объекта...
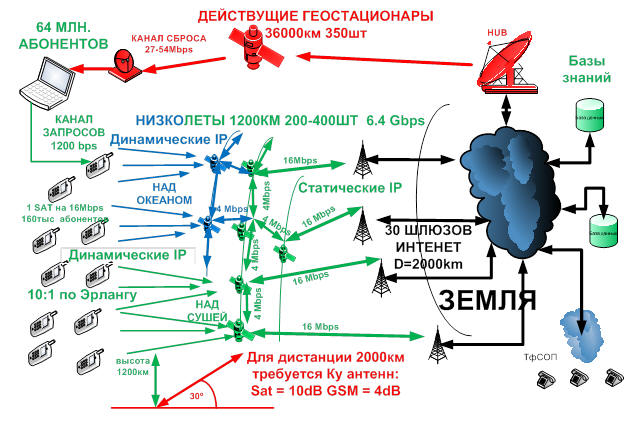
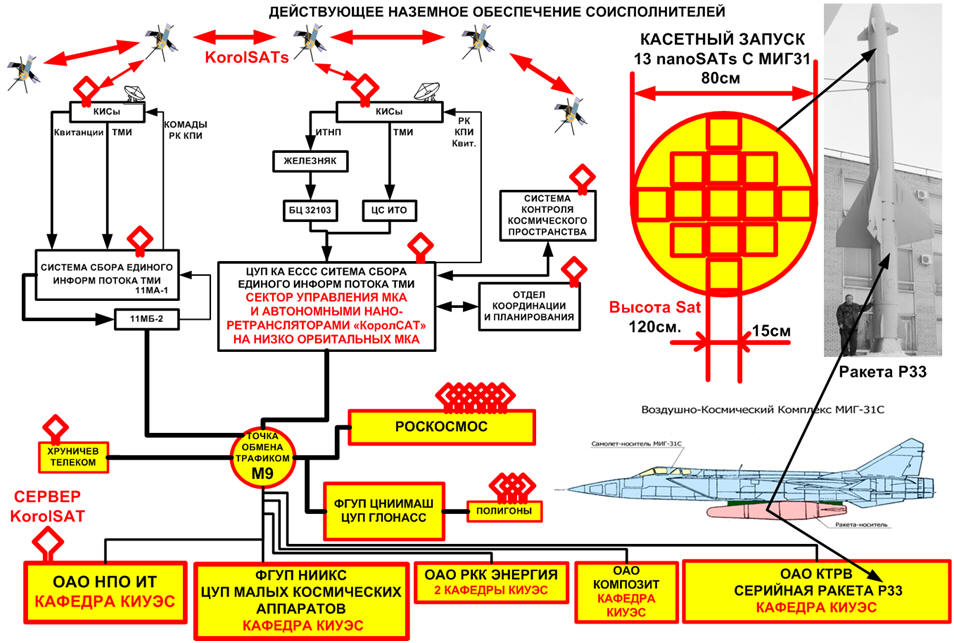
Справка: www.kimes.ru
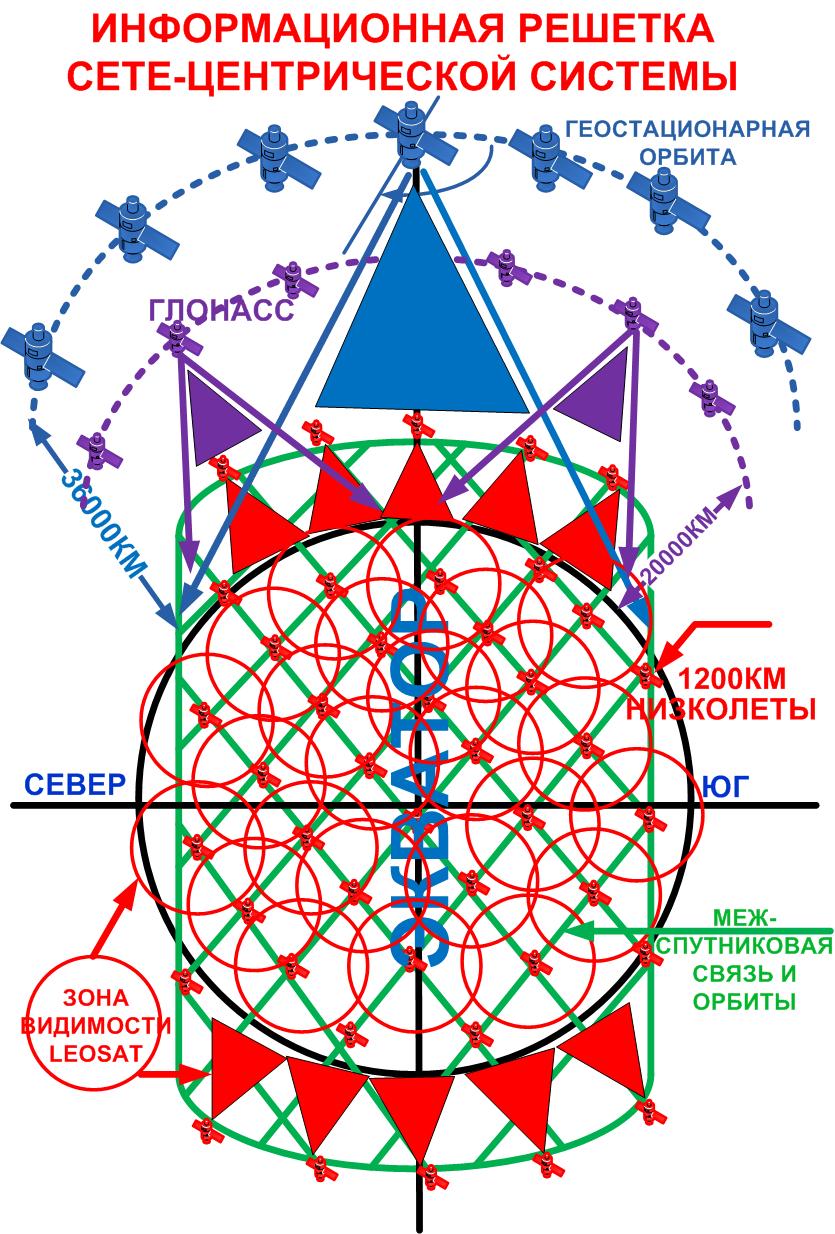
Есть конечно, примеры дальней космической связи на ШПС, но там за счет алгоритмитики и обмена энергии на полосу получены отношенияEb/No близкие к -1dB, но не -10dB пока. В целом работа со значениями Eb/No= от -10 до -6dB только начинаются и всем связистам мира хватит места для успешного творчества для личного и блага и процветания Ваших фирм.
Колоколо-подобный спектр имеют все GMSK виды манипуляции. На рисунке ниже по новой методике подавления МСИ показанные спектры сигналов которые имеют явно выраженный прямоугольный спектр независимо от вида 2-х уровневой манипуляции. Причем превышение уровня над 0dBm (1мВатт или 95% энергии сигнала) доходит до 6dB.
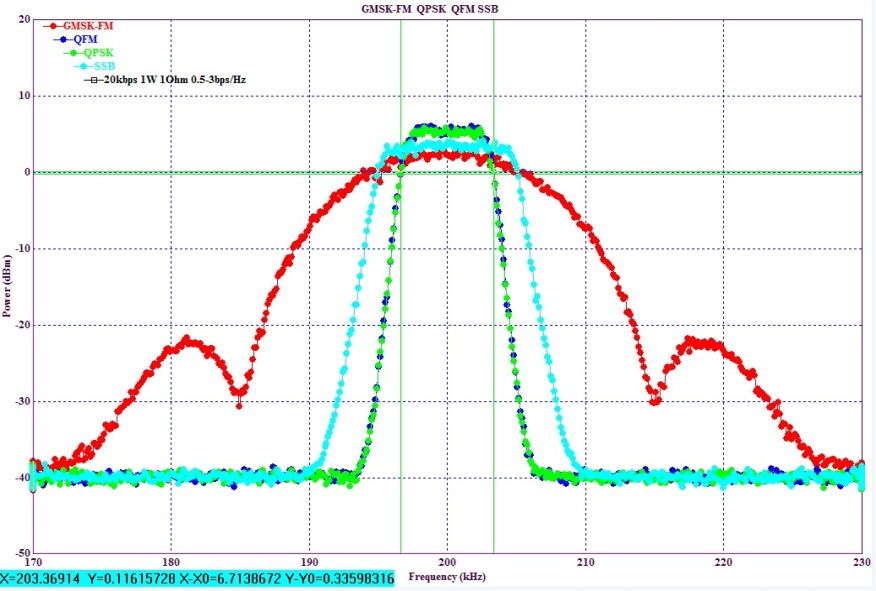
Приведем самый характерный пример расчета баланса энергии радиотрасс для расстояния 10км с мощностью излучения 10 милливатт для колокольных спектров. При использовании антенн на передающей и приемной стороне с усилением 3dB (диполь Герца или ¼ штырь с 3-мя противовесами).
| п/п | Частота (МГц) | Полоса по требованиям ГКРЧ (кГц) России | Чувствительность приемник (-dBm) | Уровень сигнала на входе приемника (мкВ) | Отношение сигнал/шум Eb/No(dB) |
| -74 | |||||
| -80 | |||||
| -83 | |||||
| -88 | |||||
| -95 | |||||
| -96 | |||||
| -104 | 3,5 |
Как видно из таблицы ни одно современное решение по теоремам Найквиста о МСИ не имеет 2.5dB отношения сигнал/шум, что эквивалентно -114dB или 0.4 мкВ. Варианты имеют скорость в полосах разрешенных ГКРЧ России 6 и 10 кГц не более 1200Бит/с, в полосах 25кГц скорость не более 9600Бит/с. Здесь же применяются скорости 6, 10 и 25 кбит/с соответственно. Это в 2-6 раза выше, чем у любого известного решения. При этом здесь (теоремы Батухтина о МСИ) спектральная эффективность равна 1-2 (Бит/с) на 1 Гц эфира, а у любого известного решения по Найквисту не более 0.1-0.38 (бит/с)/Гц. Рассмотрим, как любой связист сегодня добивается работоспособности своей продукции на дистанции 10км при типовом отношении сигнал/шум (Eb/No) 8-10dB (эквивалентно -77-66dBm или 25-150мкВ) в разных полосах безлицензионных частот от 13 до 430МГц. Для конкретики рассчитаем при чувствительности приемника -66dB. Производитель проводных и радиомодемов из-за низкого качества связи или завышают мощность излучения и нарушают требования ГКРЧ или вынуждены применять большие коэффициенты усиления антенн. Поэтому стоимость готовой продукции массового беспроводного средства связи в комплекте (антенна, усилитель мощности, рация, модем, контроллер пакетирования и телеметрического управления) практически у всех производителей жаргонно называемых «радиомодемов» очень высока и находиться в рамках трех номиналов: Мощность до 500 милливатт до 150$. Мощность до 5 ватт до 400$ на скорость 1200Бит/с. Мощность 25 ватт до 1500$ на скорость 9600Бит/с. И такой стоимости виновата описка Найквиста в названии теорем о МСИ.
| п/п | Частота (МГц) | Передатчик (dBm, милливатт) | Усиление Антенн (dB) |
| 10, 10 | |||
| 28, 700 | |||
| 20, 100 | |||
| 30, 1000 | |||
| 30, 1000 | |||
| 30, 1000 | |||
| 37, 5000 |
Обратите внимание и на то, что модернизация широко известных цифровых каналов передачи данных и создание новых ранее неизвестных с улучшенными характеристиками связи (помехоустойчивость и спектральная эффективность) является пустой и нейтральной (!) нишей рынка сбыта на планете. Общий вид радиоканала без сетевого контроллера пакетирования любого производителя микросхем радиокристаллов имеет такой вид:
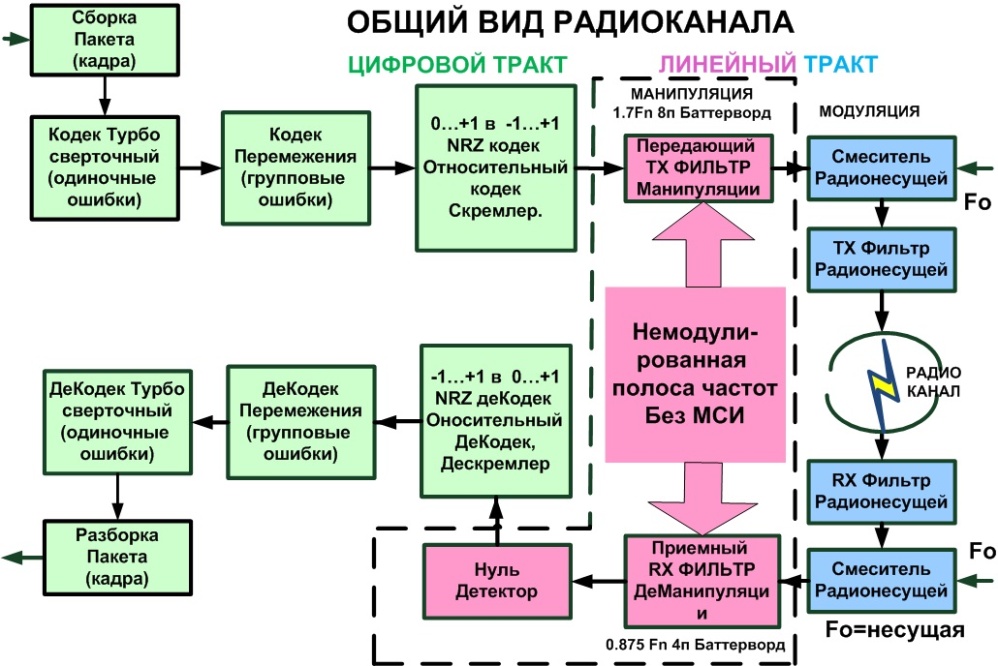
Зеленые блоки (турбосверточный кодек, кодек перемежения и кодек NRZ со скремблером) это чисто цифровые блоки, которые легко реализуются программно в микропроцессорах любой платформы. Цифровые блоки подают сигнал на фильтр низких частот (красные блоки) перед манипулятором, чтобы сгладить (окатать) фронты меандроподобных синхронных цифровых сигналов данных в проводных каналах связи. Затем идут синие блоки модуляторов (АМ, ЧМ, ФМ и т.д.). Аналогично фильтр низких частот есть на приемной стороне после демодулятора как проводных, так и беспроводных каналах. Эти фильтры низких частот на передаче и приеме являются фундаментальными преобразователями между миром цифровой техники и миром аналоговой синусоподобной волн как в физической духпроводной линии (оптике), так на радио частотах.
Примениение новых теорем о МСИ позволит выполнить модернизацию имеющихся средств проводной и беспроводной связи путем замены (перепрошивки) только передающих и приемных фильтров низких частот для устранения ошибки Найквиста в теореме о межсимвольной интерференции при цифровой передаче данных. Любая система связи любого производителя проводных и беспроводных модемов не подвергается при этом ни каким иным изменениям по типу манипуляции, модуляции и протоколу пакетирования. Изменяются только фильтры перед модулятором в передатчиках и после детектора в приемниках (красные блоки). Выигрыш после такой замены по помехоустойчивости на 6-10dB, что эквивалентно в 4-10 раз по мощности сигнала. Как распорядиться этим выигрышем, уменьшить усиление антенн, расширить зону покрытия, или обеспечить большую дальность по проводу будете решать сами производители.
ВЫВОД.
Инженерам связи планеты мешает межсимвольная интерференция, как элементарная ошибка проектирования аппаратуры связи. И собственно все усилия борьбы цифровых методов с групповыми и одиночными ошибками в канале связи сегодня тратятся не на уничтожение реальных эфирных (проводных) помех (затухания), а на тривиальную аппаратную ошибку в аппаратуре связи в основной немодулированной полосе частот.
Дата добавления: 2015-12-26; просмотров: 6180;
