Формула Хартли. Количество информации

Попытки количественного измерения информации предпринимались неоднократно. Первые отчетливые предложения об общих способах измерения количества информации были сделаны Р. Фишером (1921 г.) в процессе решения вопросов математической статистики. Проблемами хранения информации, передачи ее по каналам связи и задачами определения количества информации занимались Р. Хартли (1928 г.) и X. Найквист (1924 г.). Р. Хартли заложил основы теории информации, определив меру количества информации для некоторых задач. Наиболее убедительно эти вопросы были разработаны и обобщены американским инженером Клодом Шенноном в 1948 г. С этого времени началось интенсивное развитие теории информации вообще и углубленное исследование вопроса об измерении ее количества в частности.

Для того чтобы применить математические средства для изучения информации, потребовалось отвлечься от смысла, содержания информации. Этот подход был общим для упомянутых нами исследователей, так как чистая математика оперирует с количественными соотношениями, не вдаваясь в физическую природу тех объектов, за которыми стоят соотношения. Например, если находится сумма двух чисел 5 и 10, то она в равной мере будет справедлива для любых объектов, определяемых этими числами. Поэтому, если смысл выхолощен из сообщений, то отправной точкой для информационной оценки события остается только множество отличных друг от друга событий и соответственно сообщений о них.

Предположим, нас интересует следующая информация о состоянии некоторых объектов: в каком из четырех возможных состояний (твердое, жидкое, газообразное, плазма) находится некоторое вещество? на каком из четырех курсов техникума учится студент?

Во всех этих случаях имеет место неопределенность интересующего нас события, характеризующаяся наличием выбора одной из четырех возможностей. Если в ответах на приведенные вопросы отвлечься от их смысла, то оба ответа будут нести одинаковое количество информации, так как каждый из них выделяет одно из четырех возможных состояний объекта и, следовательно, снимает одну и ту же неопределенность сообщения.
Неопределенность неотъемлема от понятия вероятности. Уменьшение неопределенности всегда связано с выбором (отбором) одного или нескольких элементов (альтернатив) из некоторой их совокупности. Такая взаимная обратимость понятий вероятности и неопределенности послужила основой для использования понятия вероятности при измерении степени неопределенности в теории информации. Если предположить, что любой из четырех ответов на вопросы равновероятен, то его вероятность во всех вопросах равна 1/4. Одинаковая вероятность ответов в этом примере обусловливает и равную неопределенность, снимаемую ответом в каждом из двух вопросов, и, следовательно, каждый ответ несет одинаковую информацию.

Теперь попробуем сравнить следующие два вопроса: на каком из четырех курсов техникума учится студент? Как упадет монета при подбрасывании: вверх «гербом» или «цифрой»? В первом случае возможны четыре равновероятных ответа, во втором – два. Следовательно, вероятность какого-то ответа во втором случае больше, чем в первом (1/2 > 1/4), в то время как неопределенность, снимаемая ответами, больше в первом случае. Любой из возможных ответов на первый вопрос снимает большую неопределенность, чем любой ответ на второй вопрос. Поэтому ответ на первый вопрос несет больше информации! Следовательно, чем меньше вероятность какого-либо события, тем большую неопределенность снимает сообщение о его появлении и, следовательно, тем большую информацию оно несет.

Предположим, что какое-то событие имеет m равновероятных исходов. Таким событием может быть, например, появление любого символа из алфавита, содержащего m таких символов. Как измерить количество информации, которое может быть передано при помощи такого алфавита? Это можно сделать, определив число N возможных сообщений, которые могут быть переданы при помощи этого алфавита. Если сообщение формируется из одного символа, то N = m, если из двух, то N = m · m = m2. Если сообщение содержит n символов (n – длина сообщения), то N = mn. Казалось бы, искомая мера количества информации найдена. Ее можно понимать как меру неопределенности исхода опыта, если под опытом подразумевать случайный выбор какого-либо сообщения из некоторого числа возможных. Однако эта мера не совсем удобна. При наличии алфавита, состоящего из одного символа, т.е. когда m = 1, возможно появление только этого символа. Следовательно, неопределенности в этом случае не существует, и появление этого символа не несет никакой информации. Между тем, значение N при m= 1 не обращается в нуль. Для двух независимых источников сообщений (или алфавита) с N1 и N2 числом возможных сообщений общее число возможных сообщений N = N1N2, в то время как логичнее было бы считать, что количество информации, получаемое от двух независимых источников, должно быть не произведением, а суммой составляющих величин.
Выход из положения был найден Р. Хартли, который предложил информацию I, приходящуюся на одно сообщение, определять логарифмом общего числа возможных сообщений N:

Если же все множество возможных сообщений состоит из одного (N = m = 1), то I (N) = log 1 = 0, что соответствует отсутствию информации в этом случае. При наличии независимых источников информации с N1 и N2 числом возможных сообщений

I (N) = log N = log N1N2 = log N1 + log N2,

т.е. количество информации, приходящееся на одно сообщение, равно сумме количеств информации, которые были бы получены от двух независимых источников, взятых порознь. Формула, предложенная Хартли, удовлетворяет предъявленным требованиям. Поэтому ее можно использовать для измерения количества информации.
Если возможность появления любого символа алфавита равновероятна (а мы до сих пор предполагали, что это именно так), то эта вероятность р = 1/m. Полагая, что N = m,

I = log N = log m = log (1/p) = – log p, (2)

т.е. количество информации на каждый равновероятный сигнал равно минус логарифму вероятности отдельного сигнала. Полученная формула позволяет для некоторых случаев определить количество информации. Однако для практических целей необходимо задаться единицей его измерения. Для этого предположим, что информация – это устраненная неопределенность. Тогда в простейшем случае неопределенности выбор будет производиться между двумя взаимоисключающими друг друга равновероятными сообщениями, например между двумя качественными признаками: положительным и отрицательным импульсами, импульсом и паузой и т.п. Количество информации, переданное в этом простейшем случае, наиболее удобно принять за единицу количества информации. Именно такое количество информации может быть получено, если применить формулу (2) и взять логарифм по основанию 2.

Тогда

I = – log2 p = – log2 1/2 = log2 2 = 1.

Полученная единица количества информации, представляющая собой выбор из двух равновероятных событий, получила название двоичной единицы, или бита. Название bit образовано из двух начальных и последней букв английского выражения binary digit, что значит двоичная единица. Бит является не только единицей количества информации, но и единицей измерения степени неопределенности. При этом имеется в виду неопределенность, которая содержится в одном опыте, имеющем два равновероятных исхода.

На количество информации, получаемой из сообщения, влияет фактор неожиданности его для получателя, который зависит от вероятности получения того или иного сообщения. Чем меньше эта вероятность, тем сообщение более неожиданно и, следовательно, более информативно. Сообщение, вероятность которого высока и, соответственно, низка степень неожиданности, несет немного информации.

Р. Хартли понимал, что сообщения имеют различную вероятность и, следовательно, неожиданность их появления для получателя неодинакова. Но, определяя количество информации, он пытался полностью исключить фактор «неожиданности». Поэтому формула Хартли позволяет определить количество информации в сообщении только для случая, когда появление символов равновероятно и они статистически независимы. На практике эти условия выполняются редко. При определении количества информации необходимо учитывать не только количество разнообразных сообщений, которые можно получить от источника, но и вероятность их получения.

Формула Шеннона

Наиболее широкое распространение при определении среднего количества информации, которое содержится в сообщениях от источников самой разной природы, получил подход. К Шеннона. Рассмотрим следующую ситуацию.
Источник передает элементарные сигналы k различных типов. Проследим за достаточно длинным отрезком сообщения. Пусть в нем имеется N1 сигналов первого типа, N2 сигналов второго типа, ..., Nk сигналов k-го типа, причем N1 + N2 + ... + Nk = N – общее число сигналов в наблюдаемом отрезке, f1, f2, ..., fk – частоты соответствующих сигналов. При возрастании длины отрезка сообщения каждая из частот стремится к фиксированному пределу, т.е.

lim fi = pi, (i = 1, 2, ..., k),

где рi можно считать вероятностью сигнала. Предположим, получен сигнал i-го типа с вероятностью рi, содержащий – log pi единиц информации. В рассматриваемом отрезке i-й сигнал встретится примерно Npi раз (будем считать, что N достаточно велико), и общая информация, доставленная сигналами этого типа, будет равна произведению Npi log рi. То же относится к сигналам любого другого типа, поэтому полное количество информации, доставленное отрезком из Nсигналов, будет примерно равно

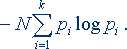
Чтобы определить среднее количество информации, приходящееся на один сигнал, т.е. удельную информативность источника, нужно это число разделить на N. При неограниченном росте приблизительное равенство перейдет в точное. В результате будет получено асимптотическое соотношение – формула Шеннона

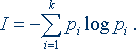
В последнее время она стала не менее распространенной, чем знаменитая формула Эйнштейна Е = mc2. Оказалось, что формула, предложенная Хартли, представляет собой частный случай более общей формулы Шеннона. Если в формуле Шеннона принять, что
р1 = p2 = ... = рi = ... =pN = 1/N, то

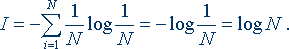
Знак минус в формуле Шеннона не означает, что количество информации в сообщении – отрицательная величина. Объясняется это тем, что вероятность р, согласно определению, меньше единицы, но больше нуля. Так как логарифм числа, меньшего единицы, т.е. log pi – величина отрицательная, то произведение вероятности на логарифм числа будет положительным.

Кроме этой формулы, Шенноном была предложена абстрактная схема связи, состоящая из пяти элементов (источника информации, передатчика, линии связи, приемника и адресата), и сформулированы теоремы о пропускной способности, помехоустойчивости, кодировании и т.д.

В результате развития теории информации и ее приложений идеи Шеннона быстро распространяли свое влияние на самые различные области знаний. Было замечено, что формула Шеннона очень похожа на используемую в физике формулу энтропии, выведенную Больцманом. Энтропия обозначает степень неупорядоченности статистических форм движения молекул. Энтропия максимальна при равновероятном распределении параметров движения молекул (направлении, скорости и пространственном положении). Значение энтропии уменьшается, если движение молекул упорядочить. По мере увеличения упорядоченности движения энтропия стремится к нулю (например, когда возможно только одно значение и направление скорости). При составлении какого-либо сообщения (текста) с помощью энтропии можно характеризовать степень неупорядоченности движения (чередования) символов. Текст с максимальной энтропией – это текст с равновероятным распределением всех букв алфавита, т.е. с бессмысленным чередованием букв, например: ЙХЗЦЗЦЩУЩУШК ШГЕНЕЭФЖЫЫДВЛВЛОАРАПАЯЕЯЮЧБ СБСЬМ. Если при составлении текста учтена реальная вероятность букв, то в получаемых таким образом «фразах» будет наблюдаться определенная упорядоченность движения букв, регламентируемая частотой их появления: ЕЫТ ЦИЯЬА ОКРВ ОДНТ ЬЧЕ МЛОЦК ЗЬЯ ЕНВ ТША.
При учете вероятностей четырехбуквенных сочетаний текст становится настолько упорядоченным, что по некоторым формальным признакам приближается к осмысленному: ВЕСЕЛ ВРАТЬСЯ НЕ СУХОМ И НЕПО И КОРКО.

Причиной такой упорядоченности в данном случае является информация о статистических закономерностях текстов. В осмысленных текстах упорядоченность, естественно, еще выше. Так, в фразе ПРИШЛ... ВЕСНА мы имеем еще больше информации о движении (чередовании) букв. Таким образом, от текста к тексту увеличиваются упорядоченность и информация, которой мы располагаем о тексте, а энтропия (мера неупорядоченности) уменьшается.

Используя различие формул количества информации Шеннона и энтропии Больцмана (разные знаки), Л. Бриллюэн охарактеризовал информацию как отрицательную энтропию, или негэнтропию. Так как энтропия является мерой неупорядоченности, то информация может быть определена как мера упорядоченности материальных систем.
В связи с тем, что внешний вид формул совпадает, можно предположить, что понятие информация ничего не добавляет к понятию энтропии. Однако это не так. Если понятие энтропии применялось ранее только для систем, стремящихся к термодинамическому равновесию, т.е. к максимальному беспорядку в движении ее составляющих, к увеличению энтропии, то понятие информации обратило внимание и на те системы, которые не увеличивают энтропию, а наоборот, находясь в состоянии с небольшими значениями энтропии, стремятся к ее дальнейшему уменьшению.

Трудно переоценить значение идей теории информации в развитии самых разнообразных научных областей.

Однако, по мнению К. Шеннона, все нерешенные проблемы не могут быть решены при помощи таких магических слов, как «информация», «энтропия», «избыточность».
Теория информации основана на вероятностных, статистических закономерностях явлений. Она дает полезный, но не универсальный аппарат. Поэтому множество ситуаций не укладываются в информационную модель Шеннона. Не всегда представляется возможным заранее установить перечень всех состояний системы и вычислить их вероятности. Кроме того, в теории информации рассматривается только формальная сторона сообщения, в то время как смысл его остается в стороне. Например, система радиолокационных станций ведет наблюдение за воздушным пространством с целью обнаружения самолета противника Система S, за которой ведется наблюдение, может быть в одном из двух состояний x1 – противник есть, x2 – противника нет. Важность первого сообщения нельзя оценить с помощью вероятностного подхода. Этот подход и основанная на нем мера количества информации выражают, прежде всего, «структурно-синтаксическую» сторону ее передачи, т.е. выражают отношения сигналов. Однако понятия «вероятность», «неопределенность», с которыми связано понятие информации, предполагают процесс выбора. Этот процесс может быть осуществлен только при наличии множества возможностей. Без этого условия, как можно предположить, передача информации невозможна.