III.2.1. Диэлектрическая поляризация полимеров: физический (молекулярно-кинетический) подход

Поведение полимеров, помещенных в постоянное или переменное электрическое поле (при отсутствии остаточной поляризации), обусловлены процессами поляризации и активной ионной проводимости в них, которые и характеризуют их диэлектрические свойства. Связь этих свойств со структурой и молекулярным движением базируется на обобщении феноменологических и молекулярно-кинетических представлений о поведении диэлектриков в электрическом поле. Такой подход реализуется в методах молекулярной физики. С другой стороны, подход технической физики (теории электрических цепей) базируется на эквивалентных электрических моделях и позволяет связать параметры, характеризующие электрическую цепь и ее элементы и измеряемые непосредственно в экспериментах, с диэлектрическими характеристиками исследуемых объектов.

Различия в терминах, подходах и методах, используемых в молекулярной и технической физике для описания многообразных и сложных процессов, протекающих в исследуемых объектах и измерительных системах при определении и анализе диэлектрических свойств, затрудняют интерпретацию получаемых результатов и требуют тщательного анализа терминологии и основных теоретических представлений, используемых в методах диэлектрической релаксации при исследовании полимеров и полимерных композиций.

а) Мгновенная деформационная и равновесная ориентационная поляризация и параметры диэлектрических свойств полимеров

Электронная и ядерная поляризация, обусловленная обратимым деформированием электронных облаков и смещением ядер атомов в электрическом поле, возможна во всех полимерах и полимерных композициях, в том числе неполярных и протекает практически мгновенно по сравнению с ориентационной поляризацией. Она не связана с молекулярным тепловым движением, т.е является нерелаксационным процессом, аналогичным мгновенно-упругой деформации в процессах механической релаксации. Ориентационная поляризация обусловлена протеканием обратимых, сравнительно медленных процессов ориентации постоянных диполей (полярных групп или звеньев и молекул полярных примесей), образованных атомами с различной электроотрицательностью. Ориентационная поляризация и обратный ей процесс деполяризации связаны с основными активационными формами молекулярного, главным образом внутримолекулярного (сегментального и группового) теплового движения, и формально имеют определенную аналогию с замедленной энтропийной упругостью цепей и связанной с ней вязко-упругостью и упруго-вязкостью. Однако, в отличие от процессов механической релаксации, протекающих в любых полимерах, диэлектрическая ориентационная, или дипольная поляризация отражают внутримолекулярное тепловое движение только в полярных полимерах, содержащих хотя бы один полярный компонент, примесь или специальную добавку (зонд). Необратимый перенос ионов в электрическом поле обусловливает активную проводимость в полимерах и оказывает существенное влияние на процесс диэлектрической релаксации, особенно при низких частотах или в постоянном поле Формально он аналогичен вязкому течению в процессах механической релаксации. Накопление электрических зарядов на границах раздела фаз (внутренних в гетерофазных полимерах) и внешних (на электродах), которое называется межфазной и электродной поляризацией соответственно, также оказывает существенное и трудно контролируемое влияние на процессы диэлектрической релаксации. Эти явления не имеют аналогов в процессах механического деформирования.

В настоящее время отсутствует достаточно строгая обобщеннаямолекулярно-кинетическая теория диэлектрической поляризации полимеров, поэтому к ним применяются, в первом приближении, теории, разработанные для жидкостей и кристаллических твердых тел. В полимере, в котором суммарный электрический момент при отсутствии электрического поля равен нулю (отсутствует сегнетоэлектрический или электретный эффект), при приложении постоянного электрического поля происходит так называемая деформационная поляризация групп и звеньев - электронные облака атомов и связей, образующих группы и звенья полимерных цепей, практически мгновенно сместятся (деформируются) в сторону положительного заряда поля, а ядра атомов сместятся в противоположную сторону с образованием наведенного (индуцированного) электрического момента (диполя). Предполагается, что вектор возникающего при этом электрического момента группы или звенаmпропорционален вектору внутренней силы (напряженности) поля F,причем коэффициент пропорциональностиα₀ характеризует деформационную поляризуемость группы или звена:

m=α_дF (2.1)

В конденсированных молекулярных системах, в том числе в полимерах, F не идентична внешней силе (напряженности) поля Е, измеряемой на пластинах проводников, на которые подается напряжение (пластинах, или обкладках конденсатора). Кроме Евнутренняя сила Fвключаетдополнительную силу F₁ (напряженность поля, создаваемую окружением группы или звена, находящимся на достаточно большом расстоянии между пластинами конденсатора, и силу F₂ (напряженность поля, обусловленную собственно группой или звеном и их ближайшими соседями). Величину F₂нельзя определить в общей форме. Если принять ее равной нулю, что допустимо в первом приближении, то в международной системе единиц (СИ) при сферической форме групп или звеньев можно записать:

F= ε₀Е + F₁=ε₀E+P/3,(2.2)

где Р – вектор электрического момента (поляризации) единицы объема вещества; ε₀ – диэлектрическая постоянная вакуума (e₀= 8,85∙10^-12 Ф/м).

Если n – число групп или звеньев в единице объема, то:

Р=nm= nα_д(ε₀E+P/3) (2.3)

С другой стороны, согласно формальной классической теории поведения диэлектрика, помещенного между пластинами конденсатора в постоянное электрическое поле, равновесное смещение зарядов, или электрическая индукция D связана с напряженностью поля материальным уравнением Максвелла. В СИ это уравнение имеет вид:

D= ε₀E+P , (2.4)

где P– наведенная обратимая поляризация, обусловленная возникновением электрического момента, индуцированного внешним полем, пропорциональная напряженности поля:

Р =χε₀E (2.6)

где: c-коэффициент пропорциональности, или диэлектрическая восприимчивость вещества.

Объединение уравнений 2.4 и 2.6 дает:

D= ε₀(1+χ)E= ε₀_sE; P=(_s-1) ε₀E (2.7)

где: _s- относительная диэлектрическая проницаемость вещества, которая характеризует его поляризуемость под действием поля по отношению к вакууму:

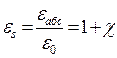(2.8).

а _абс – абсолютная диэлектрическая проницаемость среды.

Комбинация уравнений 2.3 и 2.7 позволяет связать равновесную поляризацию единицы объема с относительной диэлектрической проницаемостью вещества уравнением Лоренца-Лоренца и с поляризуемостью групп или звеньев сферической формы уравнением Клаузиуса-Мосотти соответственно :

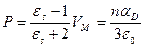(2.9)

Пересчет поляризации в единице объема на объем одного моля V_М групп или звеньев, равный частному от деления молекулярной массы М на плотность ρ, или на число Авогадро N_А, равное 6,06∙10²³, дает аналогичные соотношения для мольной поляризации Р_М, равной, при отсутствии постоянных диполей, мольной рефракции R_М:

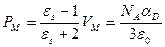(2.10)

Из соотношений 2.9 и 2.10 следует, что чисто феноменологическая постоянная, введенная в закон Максвелла (Р в выражении 2.7) имеет четкий молекулярный смысл и непосредственно связана с поляризацией молекул.

Если группы или звенья являются полярными и обладают постоянным электрическим моментом, т.е. центры положительных и отрицательных зарядов в них не совпадают, то в электрическом поле они подвергаются действию крутящего момента m:

m= - μFsinφ (2.11)

где: μ – дипольный момент группы или звена, равный произведению заряда на расстояние между центрами; F –напряженность внутреннего поля; φ – угол между направлениями момента диполя и электрического поля.

С учетом хаотического теплового движения полярных групп или звеньев препятствующего их повороту под действием электрического поля (ориентации по полю), возникающий средний электрический момент равен:

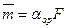, (2.12)

Коэффициент пропорциональности, или ориентационная составляющая поляризуемости, рассчитанная Дебаем, равна: α_ор= 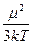, где: k – постоянная Больцмана, Т – абсолютная температура.

С учетом деформационной и ориентационной составляющих поляризуемости выражение для обобщенной мольной поляризации (уравнение Клаузиуса-Мосотти-Дебая) в системе СИ принимает вид:

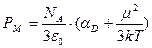(2.13)

Таким образом, в соответствие с атомно-молекулярными представлениями, поляризация полимерных диэлектриков в электрическом поле в решающей степени определяется природой электронных облаков в них, типом, количеством и тепловой подвижностью полярных групп или звеньев (диполей). В идеальном случае неполярнго полимера, в котором отсутствуют полярные группы и примеси, свободные ионы и другие заряды, а также границы раздела фаз, должна иметь место только деформационная поляризация (электронная и ядерная), причем вклад последней в общую поляризацию незначителен. Процессы поляризации при этом протекают практически мгновенно и не носят релаксационного характера, т.е. должны отсутствовать температурно-временные или частотные зависимости параметров диэлектрических свойств. Относительная диэлектрическая проницаемость таких полимеров 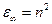, где n – коэффициент преломления света. Величина e_¥ связана с мольной рефракцией полимеров R_M, которая может быть рассчитана методом групповых вкладов или другими методами с использованием соотношений:

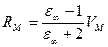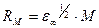; , (2.14)

где V_M, R_M – мольный объем и молекулярная масса повторяющегося звена полимера.

В идеальном случае полярного полимера, имеющего постоянные диполи (полярные группы и звенья) при отсутствии свободных носителей зарядов и границ раздела, наряду с деформационной поляризацией, которая является определяющей при высоких частотах, при сравнительно низких частотах проявляется также дипольная, или ориентационная поляризация (Р_op), обусловленная ориентацией диполей в электрическом поле. При наличии нескольких типов диполей в полимерах дипольная поляризация в них подразделяется на дипольно-сегментальную, обусловленную ориентацией диполей главной цепи, и дипольно-групповую, обусловленную ориентацией диполей боковых или концевых групп или звеньев, а также полярных молекул низкомолекулярных компонентов и примесей.

Если к идеальному полярному диэлектрику, не имеющему остаточной поляризации, не содержащему свободных носителей зарядов (ионов и электронов) и дипольная поляризация которого является линейной функцией напряженности поля, мгновенно приложить постоянное поле напряженностью Е₀, то электрическое смещение D в любой момент времени t равно:

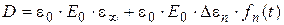(1.10)

Первый член этого уравнения соответствует мгновенному отклику диэлектрика на приложенное поле, т.е. деформационной поляризации, мерой которой является e_¥, а второй – медленному вкладу от дипольной поляризации, где 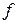_n(t) – кинетическая функция отклика, а 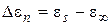- предельный вклад дипольной поляризации в относительную диэлектрическую проницаемость. Для линейных процессов дипольной поляризации скорость, с которой достигается ее предельное равновесное значение, пропорциональна степени ее отклонения от равновесия, что соответствует процессам линейной релаксации:

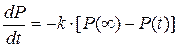(1.11)

где: k – коэффициент пропорциональности, или константа скорости, обратная величина которой 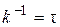называется временем релаксации данного процесса. Макроскопическое время релаксации (t_м) в общем случае не равно времени релаксации дипольной ориентации t: 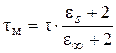(по Дебаю – … – Лоренцу) или 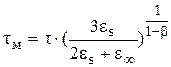(Формула Коулу-Коулу). P(¥) – предельная (равновесная) наведенная поляризация, равная .

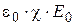Интегрирование уравнения (1.11) по времени дает интегральное выражение для кинетики дипольной поляризации:

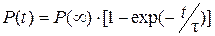(1.12)

Таким образом, кинетическая функция диэлектрического отклика от дипольной поляризации:

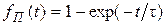(1.13)

При t®0 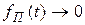, при t®¥ 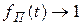, а при t=t функция 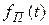претерпевает перегиб и в этой области изменяется наиболее резко. При мгновенном отключении постоянного поля от идеального полярного диэлектрика кинетическая функция спада поляризации (деполяризации):

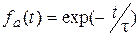(1.14)

а кинетика дипольной деполяризации описывается уравнением:

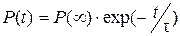(1.15)

Время релаксации дипольной поляризации t равно времени в течение которого предельная ориентационная поляризация после отключения тока уменьшается в e раз. Величина t характеризует кинетику процессов поляризации и деполяризации, и для конкретного процесса, протекающего в идеальном полярном полимере зависит только от температуры. Эта зависимость описывается уравнением Аррениуса (вдаль от области стеклования):

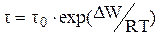(1.16)

где: t₀ – предэкспоненциальный множитель, DW – энергия активации процесса дипольной поляризации, R – газовая постоянная, Т – абсолютная температура,

или уравнением ВЛФ (вблизи области стеклования):

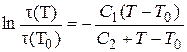(1.17)

где: (Т), (Т₀) - время релаксации при некоторой температуре Т и при стандартной температуре (температуре приведения) Т₀ соответственно; С₁, С₂ – константы, зависящие от выбора Т_{0 (}если Т₀=Т_С, то С₁=17,44; С₂=54,4 К; t(T_C)=10¹³c).

Поскольку наведенная поляризация диэлектрика характеризует накопление в нем результирующего заряда Q (P=Q), то производная 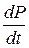соответствует поляризационному (емкостному или зарядному) току i, который в начальный момент приложения напряженности поля имеет максимальное значение, а затем спадает во времени в соответствии с уравнениями 1.11 и 1.12:

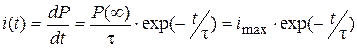(1.18)

При мгновенном отключении напряженности поля возникающий в процессе деполяризации разрядный ток будет изменяться по этому же закону.

Если к идеальному полярному диэлектрику прикладывать ступенчато возрастающую напряженность поля Е_i через заданные периоды времени t_i, то в соответствии с принципом суперпозиции Больцмана происходит суммирование электрических смещений:

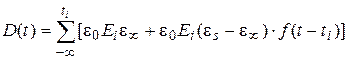(1.19)

Если напряженность поля изменяется непрерывно во времени, то общее дифференциальное уравнение для электрического смещения в идеальном полярном диэлектрике имеет вид [Лущ. C.66]:

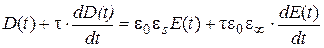(1.20)

Из этого уравнения для напряженности поля, изменяющейся по синусоидальному закону:

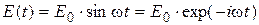(1.21)

где: w - круговая частота (периодическая частота 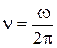); E₀ – амплитудное значение напряженности поля; .

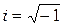Дебаем впервые были получены выражения для комплексной диэлектрической проницаемости e* и ее реальной и мнимой компонент (e¢ и e²) как функций круговой частоты приложения напряженности поля:

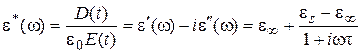(1.22)

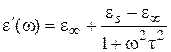(1.23)

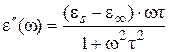(1.24)

При этом e¢ как действительная часть комплексной диэлектрической проницаемости характеризует соответственно поляризацию диэлектрика и запасенную энергию электрического поля и соответствует относительной диэлектрической проницаемости, а e² как мнимая часть комплексной диэлектрической проницаемости характеризует рассеивание энергии электрического поля в процессе поляризации в виде тепла, и называется коэффициентом, или фактором диэлектрических потерь; e_s и e_¥ - наибольшее и наименьшие значения e¢, определяемые способностью полимеров к деформационной и ориентационной поляризации и только к деформационной поляризации при частоте w®0 и w® соответственно.

В общем случае e*(w) является комплексным Фурье–преобразованием кинетической функции диэлектрического отклика 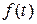. По Дебаю 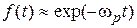, где 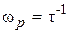. В реальных полимерных системах возможен степенной вид функции отклика:

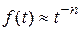(t<t) или 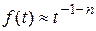(t>t)/

При этом e*(w) [ ].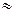

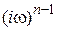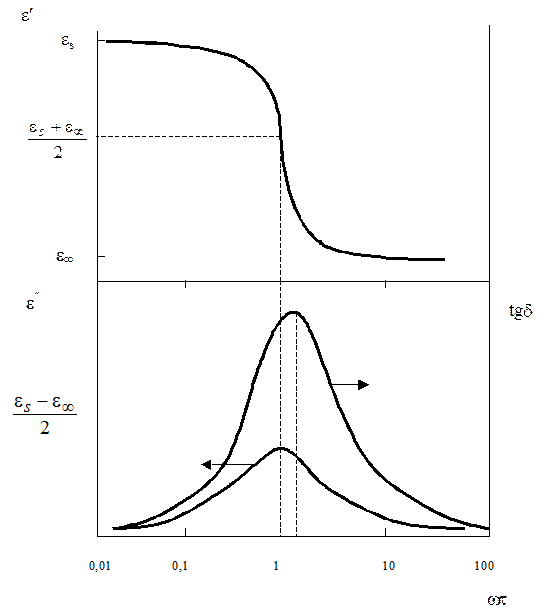
В дебаевской модели область частот, в которой wt®1, соответствует дисперсии e¢ (резко выраженной зависимости e¢ от w) и пику потерь (резко выраженной зависимости e² от w). При этом в характерной точке, соответствующей wt=1, т.е. в точке перегиба e¢ и в точке максимума e² их

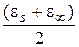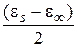величины равны и соответственно (Рис. 1.1).

Рис. 1.1. Зависимости ε¢, ε²и tg d от wt для дебаевской модели дипольной поляризации с одним временем релаксации

Возникающий между векторами электрического смещения D и напряженности поля Е при дипольной поляризации в гармоническом поле сдвиг по фазе ( 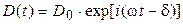) характеризуется углом d, тангенс которого 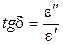и характеризует величину диссипации (рассеяния) энергии поля в процессе поляризации. Зависимость tgd от произведения wt имеет вид:

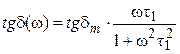(1.25)

где: tgd_m – максимальное значение tgd, равное:

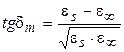(1.26)

Время релаксации t₁ в уравнении 1.25 отличается от времени релаксации t, входящего в формулы 1.23 и 1.24 и связано с ним соотношением:

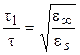(1.27)

Удобным способом изображения частотных зависимостей e¢ и e² в области дисперсии пика потерь является использование круговой диаграммы Коула-Коула [ ], уравнение которой, связывающее e¢ и e², получается объединением соотношений для их частотных зависимостей. При использовании соотношений Дебая (уравнения 1.23 – 1.24) диаграмма Коула-Коула для идеального полярного диэлектрика представляет собой полуокружность, центр которой расположен на оси e¢ с координатой 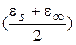, а радиус равен 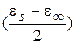(Рис. 1.2).

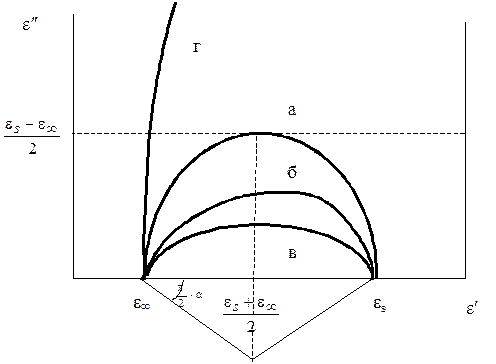
Рис. 1.2. Круговые диаграммы в области дисперсии e¢ и пика e² при отсутствии (а) и наличии спектра времен релаксации (б, в), описываемого соотношением Вильямса-Чатта (б) и Коула-Коула (в); г- диаграмма при значительном вкладе потерь от проводимости

Уравнение этой окружности имеет вид:

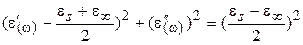(1.28)

Процессы дипольной поляризации реальных полярных полимеров в переменном электрическом поле и, следовательно, параметры их диэлектрических свойств, как правило, не подчиняются идеализированным уравнениям Дебая (1.23, 1.24, 1.28) из-за мультиплетности, т.е. наличии нескольких типов дипольно-сегментального и дипольно-групповых процессов дипольной ориентации и набора (спектра) времен релаксации для каждого из этих процессов со своим распределением времен релаксации. Мультиплетность релаксационных процессов дипольной поляризации и наличие спектров времен релаксации обусловлены многообразием типов диполей в полимерах и различием в их окружении и взаимодействием с соседями, влияющим на их тепловую подвижность.

Для описания поведения реальных полярных полимеров в электрическом поле предложено несколько эмпирических соотношений, позволяющих учитывать наличие и характер спектров времен релаксации. Так, для случая одного типа релаксационного процесса и одного спектра времен релаксации предложено соотношение Коула-Коула:

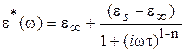(1.29)

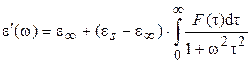(1.30)

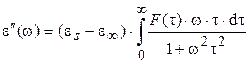(1.31)

где: n – коэффициент, учитывающий ширину распределения времен релаксации и лежащий в интервале от 0 до 1 (при n=1 эти соотношения превращаются в уравнение Дебая с одним временем релаксации;

F(t) - функция распределения времен релаксации .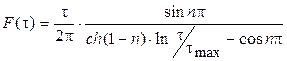

Диаграмма Коула-Коула для этого случая сохраняет симметричность полуокружности, но координаты центра смещены с оси e¢ (см. рис. 12 в), окружность имеет центр в точке с координатам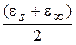и и

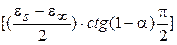, а ее радиус равен: 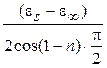. Максимальное значение e² при этом равно:

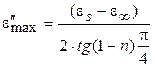(1.32)

Фуосс и Кирквуд предложили для этого случая другую функцию распределения F(t) [ ]:

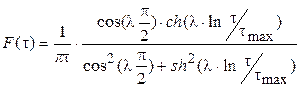(1.33)

где: l - параметр распределения, связанный с параметром 1-n соотношением:

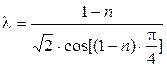(1.34)

Частотная зависимость e² при этом описывается простым соотношением:

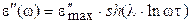(1.35)

причем 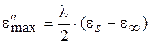(1.36)

Асимметричная форма диаграммы Коула-Коула (см. рис. 1.2 б) описывается с помощью соотношения Вильямса-Уотта, основанного на использовании функции спада поляризации в виде 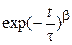, где b - параметр распределения времен релаксации, изменяющийся от 0 до 1. При b=1 это выражение превращается в функцию Дебая с одним временем релаксации.

Универсальным соотношением, используемым для описания поведения реальных полимеров, является формула Гаврильяка-Негами, представляющая собой комбинацию вышеприведенных соотношений и имеет вид для e(w) [ ]:

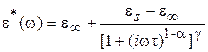(1.37)

где: g - параметр, характеризующий асимметричность F(t).

При сверхвысоких частотах ( 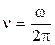>1,0 ГГц) возможно проявление резко выраженных частотных зависимостей деформационной (электронной и ядерной) поляризации и потерь вследствие эффекта резонанса, проявляющегося в колебательных системах, которыми являются атомы и связи (атомные ядра и электронные облака). При частоте внешнего поля, равной собственной частоте колебаний такой системы (n=n_р), она переходи в резонансное состояние (Рис. 1.3).

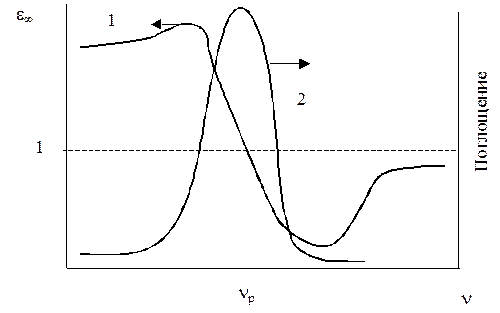
Рис. 1.3. Частотные зависимости e¥(1) и поглощения (2) в области электронно-ядерного резонанса при сверхвысоких частотах (n>1,0 ГГц)

При приближении к n_р наведенный момент и, следовательно, e_¥ возрастает. При n>n_р e_¥ резко падает до величины меньше 1, вследствие проявления индуктивности в колебательной системе, а затем проходит через минимум , приближаясь к 1. В области резонанса наблюдается узкий и высокий пик поглощения энергии.

При сверхвысоких частотах длина волны электрического поля меньше размеров образцов и напряженность поля в материале неоднородна по объему, что затрудняет прямое определение показателей их диэлектрических свойств. Поэтому для исследования электронно-ядерных резонансных эффектов в диэлектриках обычно используют методы оптической (инфракрасной и ультрафиолетовой) спектроскопии, а диэлектрическую спектроскопию применяют для исследования сравнительно медленных (релаксационных) процессов ориентационной поляризации при значительно более низких частотах. Кинетические параметры этих процессов, в первую очередь времени релаксации процессов дипольно-ориентационной поляризации, определяются температурой.

Если температурные зависимости времени дипольной релаксации в заданном температурном интервале подчиняются уравнениям Аррениуса (1.16) или ВЛФ (1.17), то введенные в вышеприведенные частотные зависимости параметров диэлектрических свойств этих уравнений дает зависимости этих параметров от температуры. При этом процессы дипольной релаксации в полимерах подчиняются принципу температурно-временной или частотной аналогии.

На рис. 1.4 а,б схематически обобщены частотные (при двух различных температурах) и температурные (при двух различных частотах) зависимости e¢ и e² идеального полярного диэлектрика с одним типом дипольной релаксации при заданном распределении времен релаксации.

Рис. 1.4. Зависимости e¢ и e² от частоты (а) при двух различных температурах (Т2>Т1) и от температуры (б) при двух различных частотах (w2>w1) для идеального полярного диэлектрика

Частоты (w_m1, w_m2) и температуры (Т_m1, Т_m2), соответствующие максимуму показателя потерь e² и точке перегиба на кривых e¢, характеризуют частоты (при заданной температуре) и температуры (при заданной частоте) релаксационного перехода для данного типа процесса дипольно-ориентационной поляризации, соответствующего условию: 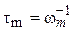. 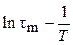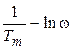По температурным зависимостям w_m и частотным зависимостям Т_m в координатах и , соответственно, может быть рассчитана энергия активации DE этого процесса, если температурная зависимость его времени релаксации описывается уравнением Аррениуса (уравнение 1.16), или константы С₁ и С₂ уравнения ВЛФ (уравнение 1.17), если оно описывает температурную зависимость времени релаксации.

Проявление в реальных полимерах мультиплетности релаксационных процессов дипольной поляризации: процесса дипольно-сегментальной поляризации, обозначаемого как a-процесс, и нескольких процессов дипольно-групповой поляризации, обозначаемых в порядке убыли их интенсивности как b-, g-, d- процессы, обусловливает проявление соответствующих релаксационных переходов (максимумов e² и перегибов на кривых e¢ на температурных зависимостях) при w-const (Рис. 1.5).

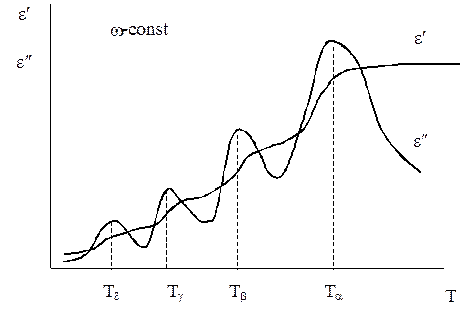
Рис. 1.5. Схематическая иллюстрация мультиплетности дипольных релаксационных переходов в полярных полимерах, содержащих несколько типов диполей, в т.ч. полярных примесей

Температуры дипольных релаксационных переходов в соответствии с принципом температурно-частотной аналогии при повышении частоты смещаются в сторону более высоких значений, накладываясь друг на друга вследствие различия в величинах энергий активации различных процессов. На частотных зависимостях e¢ и e² полярных полимеров области релаксационных (дисперсий e¢ и пиков e²), соответствующие мультиплетным процессам дипольной ориентации, проявляются только при температуре, при которой разморожена тепловая подвижность данный диполей, но заморожена подвижность более крупномасштабных диполей, т.е. область a-перехода проявляется только при Т>Т_a, b-перехода – при Т_b>Т>Т_ab и т.д.

Таким образом, определив методами диэлектрической спектроскопии Т - w или Т – t зависимости компонентов комплексной диэлектрической проницаемости (e¢, e², tgd) полярных полимеров, можно получить полную информацию о характеристиках диполей и процессах дипольной поляризации, а в более широком смысле – о молекулярном тепловом движении в полимерах: интенсивности релаксационного процесса (e_s - e_¥), времени релаксации (t), функции и параметров его распределения [F(t), a, b, g, d], областях дисперсии и диэлектрических потерь, температур дипольных релаксационных переходов, энергии активации процессов. Кроме того, контроль, в том числе дистанционный, за этими показателями, чувствительными к молекулярной, надмолекулярной и фазовой структуре полимеров и полимерных композиций позволяет использовать диэлектрическую спектроскопию как эффективный метод контроля за химическими и физическими превращениями в них под воздействием факторов окружающей среды и определения самих этих факторов.

Очевидно, что эти возможности диэлектрической спектроскопии могут быть эффективно и корректно использованы только в том случае, если будут учтены другие процессы, протекающие в исследуемых материалах, ячейках или датчиках и влияющие на получаемые результаты, их обработку и интерпретацию. К таким процессам относится движение носителей свободных зарядов (электронов и ионов), определяющее активную проводимость диэлектрика, а также различные поверхностные и электрохимические эффекты в них, в частности, образование ионных слоев на границе раздела фаз в материале и вблизи поверхности электродов.

Перенос электронов в полимерах и их электронно-дырочная проводимость может проявляться только при наличии сопряжений p-электронов, образовании донорно-акцепторных комплексов или комплексов с переносом зарядов [ ]. Большинство реальных полимеров содержат только подвижные ионы, концентрация которых определяется содержанием ионогенных групп и примесей и способностью их к диссоциации на ионы. Перенос ионов определяет активную электрическую проводимость полимеров, характеризуемую удельной объемной проводимостью g_v, обратной удельному объемному сопротивлению r_v, а также все поверхностные и электрохимические эффекты в них.

При напряженности электрического поля Е, количестве ионов i-го типа N_i в единице объема полимера и величине их зарядов q_i:

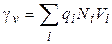(1.37)

где: V_i – скорость движения i-тых ионов в поле Е.

Для линейных сред V_i пропорционально Е:

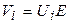(1.38)

Коэффициент пропорциональности U_i, характеризующий подвижность ионов зависит, главным образом, от плотности упаковки цепей и молекулярной (сегментальной и групповой) подвижности (внутренней вязкости)полимеров, т.е. от их фазового и реологического состояния, определяемого природой полимера и температурой. В первом приближении зависимость подвижности ионов от внутренней вязкости может быть описана законом Стокса для движения сферической частицы радиусом r_i под действием силы q_iE в среде с вязкостью h:

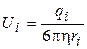(1.39)

Комбинируя уравнения 1.37 – 1.39 с уравнением Эйнштейна-Стокса для зависимости коэффициента диффузии ионов D_i от внутренней вязкости 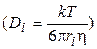дает уравнение Эйнштейна-Нернста:

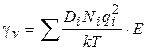(1.40)

Т.к. температурные зависимости h и D_i для полимеров описываются обычно уравнениями Аррениуса или ВЛФ (см. уравнения 1.16-1.17), то эти же уравнения применимы для описания температурных зависимостей g_v в заданном состоянии полимерного диэлектрика. В области релаксационных переходов зависимости g_v (Т) претерпевают характерные изменения.

Активная электрическая проводимость полимеров обусловливает возникновение дополнительных диэлектрических (омических) потерь в них, вклад которых в e¢¢ и tg d обратно пропорционален частоте и может быть рассчитан по соотношениям:

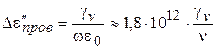(1.41)

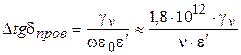(1.42)

С увеличением вклада активной проводимости в показатели диэлектрических потерь резко изменяется характер их частотной зависимости (Рис. 1.6), и при 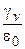>3e_s величина e² полностью определяется g_v.

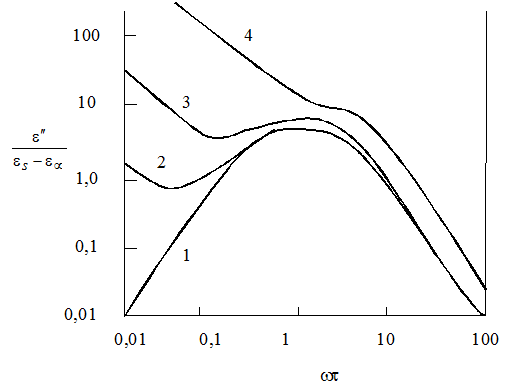
Рис. 1.6. Влияние удельной проводимости gv на частотную зависимость e² при 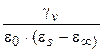равном: 0 (кривая1); 0,1 (2); 1(3); 10 (4)

С увеличением g_v диаграмма Коула-Коула превращается практически в вертикальную линию, пересекающую ось e¢ в точке e_¥ (см. рис. 1.2., кривая 2).

Подвижность ионов может не только вызывать увеличение показателей диэлектрических потерь за счет вклада проводимости, но и влиять на величину e¢ за счет эффекта поляризации на границе раздела фаз в гетерофазных системах (эффекта Максвелла-Вагнера). Вклад этого эффекта в e зависит от геометрической формы фаз 1 и 2 и разности произведений их диэлектрической проницаемости и удельной проводимости 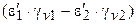. Он учитывается в различных моделях, используемых для расчета диэлектрической проницаемости гетерогенных сред по свойствам фаз, их объемному соотношению, характеру распределения и взаимодействия по границе раздела фаз [ ].