III.1.3. Электрическая емкость

В случае электростатического равновесия потенциал проводника одинаков на всем его протяжении. Это, в частности, следует из того факта, что внутри проводника поле равно нулю и, в соответствии с (1.16), разность потенциалов между его отдельными точками отсутствует.

Емкостью уединенного проводника называется величина заряда, необходимая для сообщения этому проводнику потенциала, равного единице, и обычно обозначается буквой C. В случае металлического шара радиуса a с зарядом q, потенциал которого, описываемый соотношением φ=q/a, становится равным единице при единичных значениях q и a. Тогда, в соответствии с определением емкости, C=a, т . е . емкость шара равна его радиусу. Отсюда следует, что емкость определяется, в первую очередь, геометрическими размерами и формой проводника, и в абсолютных единицах измерения емкость должна иметь размерность длины, причем емкость уединенного шара диаметром 1 см равна 1 см . Поскольку в СИ емкость равна отношению заряда к потенциалу, единица заряда (кулон ) в 3∙10 ⁹раз больше, а единица потенциала (вольт ) в 300 раз меньше, чем в абсолютной системе, то единица емкости в СИ (фарада, Ф ) в 9∙10 ¹¹ раз больше, чем в абсолютной системе, т.е. 1Ф=9∙10¹¹ см, 1 мкФ = 9∙10⁵ см , 1 пФ =0,9 см .

Рассмотренный случай уединенного проводника является предельным для его формы при отсутствии влияния соседних тел. Если вблизи заряженного проводника находятся другие проводящие тела, даже не имеющие вначале заряда, распределение заряда в заряженном теле будет другим, а в соседних телах за счет электростатической индукции возбудятся разноименные заряды. В неподвижной системе таких проводников распределение зарядов и потенциала будет равновесным, и соответствовать уравнению Лапласа (1.22). Понятие емкости при этом расширяется, и ее расчет становится достаточно сложным.

Наиболее распространен и изучен вопрос о емкости конденсаторов, представляющих собой системы, состоящие из двух проводников, или обкладок, разделенных в пространстве. Под емкостью конденсатора понимается отношение заряда q на проводниках к их разности потенциалов (φ₂-φ₁):

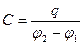. (1.25)

При этом под зарядом конденсатора q понимается абсолютная величина равных по величине и противоположных по знаку зарядов, расположенных на обращенных друг другу поверхностях проводников.

Оценим емкость плоского конденсатора, представляющего собой систему двух параллельных проводящих обкладок (пластин), разделенных зазором d. Если размеры обкладок существенно превышают зазор d, поле между ними можно считать равномерным и пренебречь краевыми эффектами вследствие неоднородности электрического поля на краях пластин. Заряд такого конденсатора q при плотности заряда на поверхности обкладок σ=q/S, где S – ее площадь, равен: q= σS. В соответствии с выражением (1.9) напряженность поля между двумя заряженными плоскостями определяется как 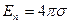, тогда разность потенциалов между пластинами в соответствие с уравнение (1.16) равна:

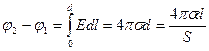, откуда: 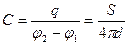(1.26)

В приведенных выражениях знак минус опушен, поскольку он определяется только знаком заряда, который может быть любым.

Аналогично, емкость цилиндрического конденсатора, образованного двумя соосными цилиндрами длиной l и радиусами внутренней и внешней обкладок r₁и r₂ соответственно, равна:

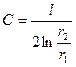(1.27)

Емкость шарового конденсатора, имеющего радиус внутренней и внешней шаровой поверхности, соответственно, R₁ и R₂, равна:

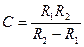(1.28)