III.1.4.Силы, действующие на проводники в электрическом поле и энергия электрического поля.

По определению, напряженность статического электрического поля E,в которое помещен заряд произвольной величины, равна силе, действующей на заряд, причем под Eпонимается напряженность поля, создаваемого всеми зарядами системы, кроме помещенного заряда q. Поскольку проводящие тела являются носителями заряда, создающего статическое электрическое поле, то между ними также будут возникать силы взаимодействия.

Рассмотрим силы, действующие на поверхностные заряды в уединенном проводнике, в котором взаимодействие зарядов сводится к их взаимному отталкиванию. В результате заряд распределяется на поверхности проводника и возникающие силы стремятся его растянуть. Действующая на единицу поверхности проводника сила f, направленная нормально к его поверхности, определяется следующими соотношениями, в которых где E определяется с помощью выражения (1.10):

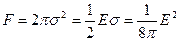, (1.29)

На практике наиболее важное значение имеют силы взаимодействия двух противоположно заряженных и расположенных параллельно плоских проводящих пластин (электродов). Для определения силы взаимодействия таких электродов необходимо установить основные представления об энергии электрически заряженных тел. При перенесении заряда в электрическом поле совершается работа A (см. соотношения 1.13-1.14). Это приводит к изменению потенциальной энергии системы зарядов dW, причем эти изменения одинаковы с совершаемой работой, связанной с измененим потенциала по величине и противоположны по знаку , т.е. dA=-qdφ=- dW. Следовательно, потенциальная энергия заряда в электрическом поле равна: W=qφ (1.30).

В частности, при взаимодействии двух точечных зарядов q₁ и q₂, находящихся на расстоянии R друг от друга, потенциал, создаваемый зарядом q₂ в точке, где находится заряд q₁, определяется выражением: φ₁=q₂/R, а потенциальная энергия заряда q1 в этой точке равна: 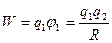(1.30)

Очевидно, что тот же результат получится для заряда q₂, т.е. выражение (1.30) определяет потенциальную энергию двух точечных зарядов, часто записывается в симметричной форме : 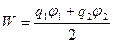и легко распространяется на случаи произвольного числа зарядов.

Определим энергию, которую запасает заряженный плоский конденсатор, разность потенциалов между пластинами которого в исходном состоянии равна 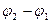. Если за счет внешнего источника конденсатор получит дополнительный заряд dq, то совершаемая при этом внешним источником работа в соответствии с выражением (1.30) будет равна:

dA=dq( 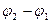). С учетом емкости конденсатора (см. соотношение1.25), последнее выражение можно записать в виде: 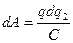. (1.31)

Полученную при заряде конденсатора энергию W можно получить интегрированием выражения (1.31), так как W=A: 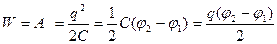. (1.32)

Для определения сил взаимного притяжения пластин заряженного конденсатора выражение (1.32) с помощью (1.26) представляется в виде: 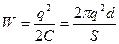. Для увеличения расстояния между пластинами заряженного конденсатора на малую величину δ необходимо совершить работу dA, приводящую к изменению энергии конденсатора на величину dW: 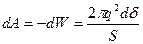.Эта работа может быть выражена через силу F, которую надо преодолеть при изменении расстояния между пластинами на величину δ: dA=-Fδd=fSδd, где f – сила притяжения, испытываемая единицей поверхности пластины конденсатора. Приравнивая два последних выражения, получаем:

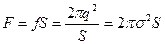, (1.33)

где σ – плотность заряда на поверхности пластин конденсатора. С учетом (1.25) и (1.26) можно выразить силу притяжения формулой: 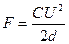(1.34), где U – напряжение.