А) Вращающие моменты, действующие на ротор синхронной машины при ее качаниях.

Вначале рассмотрим параллельную работу синхронного генератора с сетью бесконечно большой мощности при периодически изменяющемся моменте на его валу.

Предположим, что генератор приводится во вращение каким-нибудь поршневым двигателем, например одноцилиндровым четырехтактным дизелем. Кривая зависимости вращающего момента такого двигателя от угла поворота в геометрических (механических) градусах показана на рис 4-91.

Рис. 4-91. Кривая вращающего момента одноцилиндрового четырехтактного дизеля.

Как видно, вращающий момент во времени периодически изменяется (период изменения равен времени, в течение которого двигатель сделает два оборота) Его можно представить в виде среднего момента М₀, определяющего нагрузку синхронного генератора, и накладывающегося на него переменного момента М_к:

М = М₀ + М_к.

Момент М_к будем называть "избыточным" или "качательным".

Избыточный момент обусловливает вынужденные колебания синхронной машины. Он представляет собой периодическую функцию времени, среднее значение которой равно нулю. Разложим его в гармонический ряд и представим в следующем виде:

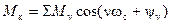, (4-90)

где М_ν — амплитуда ν-й гармоники избыточного момента;

ψ_ν — ее фазный угол;

v — порядок гармоники или число импульсов вращающего момента за один оборот;

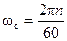— средняя (синхронная) механическая угловая частота.

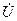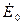Постоянный момент М₀ соответствует постоянной мощности ω_сМ₀, а следовательно, постоянному углу θ₀ между векторами и . Переменный момент М_к создает механические колебания ротора (и его полюсов), которые вызовут колебания вектора 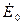относительно вектора 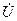напряжения сети (рис. 4-92), что в свою очередь вызовет колебания тока и мощности синхронного генератора.

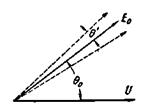
Рис. 4-92. Колебания вектора 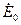относительно вектора .

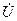Если в частном случае принять, что вращающий момент, приложенный к валу генератора со стороны первичного двигателя, постоянен и равен М₀, т е среднему значению рассмотренного ранее момента, то, очевидно, частота вращения ротора будет постоянной и никаких колебаний ее не будет В этом случае вращающий момент первичного двигателя будет уравновешиваться, если пренебречь потерями, только электромагнитным моментом генератора;

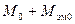
или

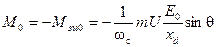. (4-91)

При колебаниях угловой частоты ротора, вызванных периодически изменяющимся вращающим моментом первичного двигателя, на вал генератора будут действовать следующие вращающие моменты.

1. Момент со стороны первичного двигателя

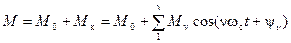. (4-92)

2. Электромагнитный момент

.

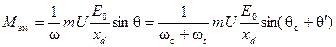Так как угловая частота колебания ω_t мала по сравнению с синхронной угловой частотой ω_с, то можем написать:

.

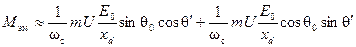Имея в виду малые колебания, т. е малое значение угла колебания или отклонения θ'. можно принять, что cos θ' 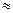1 и sin θ' 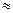θ', и считать приближенно электромагнитный момент, кГ·м,

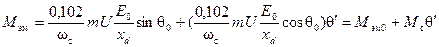, (4-93)

где М_с — удельный, а М_cθ' — полный синхронизирующие моменты

3. Момент сил инерции всех вращающихся частей агрегата (первичного двигателя и генератора) может быть найден следующим образом.

Обозначим через J момент инерции вращающихся частей агрегата, тогда кинетическая энергия, запасенная этими частями, будет равна:

.

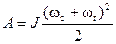Взяв первую производную энергии А по времени и разделив ее на угловую частоту ω_с + ω_t, найдем искомый момент сил инерции

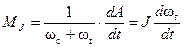. (4-94)

Механическая угловая частота колебания при р парах полюсов машины равна:

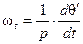. (4-95)

Из (4-94) и (4-95) получаем:

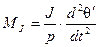. (4-96)

4. Успокоительный момент, создаваемый в результате взаимодействия поля и токов, наведенных им в успокоительной обмотке, уменьшает механические колебания ротора, что и дало повод назвать короткозамкнутую обмотку на роторе успокоительной. Она при качаниях вместе с ротором вращается то быстрее, то медленнее поля, следовательно, относительно поля имеет то отрицательное, то положительное скольжение. Это переменное скольжение

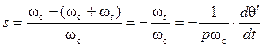. (4-97)

Успокоительный момент, называемый также асинхронным, при малых скольжениях приближенно можно считать пропорциональным скольжению:

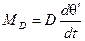, (4-98)

где D — коэффициент пропорциональности, кг_·м_·с.

Таким образом, уравнение вращающих моментов, действующих на ротор синхронной машины при ее качаниях, получается в следующем виде:

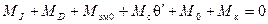. (4-99)

Так как в этом уравнении М_эм0 = -M₀, то, подставляя в него найденные выражения для отдельных моментов, получим:

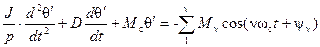. (4-100)

Решение полученного линейного дифференциального уравнения, коэффициенты которого принимаются постоянными, как известно, не представляет затруднений. С формальной стороны оно ничем не отличается от дифференциального уравнения колебательного процесса чисто механической системы, в которой роль синхронизирующего момента играет момент упругой силы какой-либо пружины, а роль момента успокоительной обмотки — момент сил трения, или, например, процесса в электрическом колебательном контуре, состоящем из индуктивности, емкости и сопротивления.

Если известна кривая избыточного момента, которая находится по индикаторной диаграмме поршневого двигателя, то можно определить ее гармоники. Решая уравнение (4-100), можно найти углы отклонения при качаниях, обусловленные каждой из этих гармоник, а затем, просуммировав их, найти результирующий угол отклонения.