III.1.1. Напряженность электрического поля .
ЭЛЕКТРИЧЕСКИЕ СВОЙСТВА ПОЛИМЕРОВ: ПОВЕДЕНИЕ ПОЛИМЕРОВ В ЭЛЕКТРИЧЕСКОМ ПОЛЕ
III.1. ОСНОВНЫЕ СВОЙСТВА ЭЛЕКТРИЧЕСКОГО ПОЛЯ
III.1.1. Напряженность электрического поля .
Электрическое поле является одним из компонентов единого электромагнитного поля и представляет собой силовое векторное поле, определяющее взаимодействие электрических зарядов, носителями которых являются электроны (отрицательно заряженные частицы), протоны (положительно заряженные частицы) и ионы - атомы или группы атомов, содержащие избыток электронов (анионы) или избыток протонов (катионы), а также тела, содержащие вышеуказанные заряженные частицы. Неподвижные заряды создают статическое электрическое поле, свойства которого описываются электростатикой. Первичные электрические заряды образуют также основу материального мира, являясь важнейшей составной частью атомов (атомных ядер и электронных оболочек) всех элементов. Поэтому каждое вещество представляет собой сложное внутреннее электрическое поле, взаимодействие которого с внешним электрическим полем определяет его электрические свойства.
Электрически заряженные тела или отдельные частицы (электроны, протоны, ионы), создающие отрицательно или положительно заряженное электрическое поле, взаимодействуют через него между собой и воздействуют на другие, даже электрически нейтральные тела или вещества. Между одноименно заряженными частицами или телами возникают силы отталкивания, а между разноименно заряженными – силы притяжения . Заряженные тела через электрическое поле (электростатическую индукцию, или наведение) возбуждают в исходно нейтральных (незаряженных ) телах противоположные заряды, вызывая силы притяжения незаряженных тел к заряженным.
Впервые количественно взаимодействие зарядов описал в 1785 г. Кулон, сформулировавший на основе экспериментальных исследований закон, согласно которому сила электростатического взаимодействия F между двумя точечными электрическими зарядами q1 и q2 прямо пропорциональна произведению величин зарядов и обратно пропорциональна квадрату расстояния r между ними:
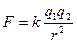(1.1)
где k – коэффициент пропорциональности, зависящий от выбора системы измерений и свойств среды, в которой происходит взаимодействие .
Силу электрического взаимодействия удобно использовать для характеристики электрического поля, создаваемого зарядами. Так, напряженность электрического поля в некоторой точке пространства может быть определена как вектор E, численно равный силе F, с которой это поле действует на единичный заряд q, помещенный в эту точку и направленный в сторону действия силы:
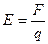(1.2)
С другой стороны, на единичный заряд q, помещенный в электрическое поле напряженностью Е, действует механическая сила:
F=Eq (1.3)
Поэтому электрическое поле считается силовым. Для наглядного представления картины электрического поля Фарадей предложил использовать силовые линии (линии напряженности) поля - кривые, касательные к которым в любой точке совпадают с направлением вектора напряженности поля E. Принято считать, что силовые линии электрического поля начинаются на положительном заряде и оканчиваются на отрицательном. Электрическое поля является незамкнутым, и его силовые линии могут уходить в бесконечность. Напряженность электрического поля подчиняется принципу суперпозиции, или наложения т.е. напряженность поля, создаваемого системой точечных зарядов, равна векторной сумме напряженностей, создаваемых каждым из зарядов в отдельности.
Как следует из закона Кулона (1.1), напряженность поля, создаваемого точечным зарядом q на расстоянии R от этого заряда, равна:
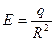(1.4)
Понимание физических процессов, протекающих на заряженных поверхностях тел и решение практических задач электростатики значительно упрощается при использовании фундаментальной теоремы Гаусса, которая утверждает, что в произвольном электростатическом поле в вакууме поток N вектора напряженности Eчерез произвольную замкнутую поверхность S равен:
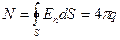(1.5)
Теорема Гаусса позволяет сравнительно просто рассчитывать напряженность электрического поля вблизи заряженных поверхностей с использование понятия плотности поверхностного заряда σ как заряда, приходящегося на единицу площади поверхности q/S. Если заряд распределен по поверхности неравномерно, то под его плотностью в данной точке понимают предельное соотношение :
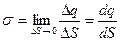(1.6)
где Δq,dq – заряд элемента поверхности ΔS, dS.
В общем случае для заряженной поверхности нормальные составляющие Еn1 и En2 вектора Eв двух смежных точках, разделенных поверхностью с плотностью заряда σ, разнятся друг от друга на следующую величину:
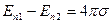, (1.7)
В частности, если поверхность плоская, и поле создается только поверхностным зарядом с плотностью σ, то оно будет иметь нормальные составляющие Еn1 и En2, одинаковые по величине и противоположные по направлению. Тогда выражение (1.7) примет следующий вид:
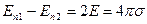, (1.8)
т.е. численное значение напряженности поля En по направлению нормали поверхностис обеих сторон заряженной плоскости равно:
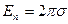(1.9)
Слагающие напряженности поля, касательные к произвольной поверхности в любой ее точке, Еt также имеют по обеим сторонам поверхности одинаковое значение, т.е. Еt1 =. Еt2.
Представление о поверхностном заряде объясняет электростатические явления, происходящие на поверхности заряженных проводников. Если сообщить проводнику заряд электронов, то, благодаря взаимному отталкиванию, они сосредоточатся на поверхности проводника в тонком приповерхностном слое, и в случае электростатического равновесия поле внутри проводников равно нулю. При этом тангенциальная составляющая напряженности поля также равна нулю. Это значит, что у проводников вектор напряженности электрического поля всегда направлен по нормали к его поверхности, а величина напряженности поля вблизи поверхности проводников любой геометрии, таких как шар или цилиндр, в соответствии с (1.7) равна:
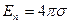(1.10)
Подобные рассуждения приводят к аналогичному результату для напряженности электрического поля между заряженными пластинами (электродами, обкладками) бесконечного плоского конденсатора. Поле в такой системе однородно, т.е. вектор Eпостоянен по величине и направлению во всех точках этого поля. Его величина должна подчиняться формуле, аналогичной (1.10):
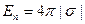, (1.11)
где |σ |– cредняя плотность поверхностного заряда обкладок конденсатора.
Дата добавления: 2015-11-26; просмотров: 2008;