Полимерные и композиционные пьезоэлектрики и электреты.
Из кристаллизующихся органических полимеров наилучшими пьезоэлектрическими и электрострикционными свойствами обладают полимеры винилиденфторида - ПВДФ (повторяющиеся звенья –CF2-CH2- обладают высоким дипольным моментом) и его сополимеры с другими сильно полярными, в первую очередь, фторсодержащими мономерами. Для получения максимального пьезоэффекта кристаллическую структуру таких полимеров подвергают ориентационной вытяжке при воздействии сильного электрического поля. Образующаяся при этом кристаллическая β-фаза обладает сегнетоэлектрическими свойствами. Сравнение пьезоэлектрических свойств мягкой и жесткой пьезокерамик типа ТЦС и ПВДФ приведены в таблице 1. Из приведенных данных видно, что полимерный пьезоэлектрик оюладает более низкими пьезоэлектрическими свойствами по сравнению с пьезокерамиками.
Таблица 1
Пьезоконстанты пьезокерамик тип ТЦС и ПВДФ
| Пьезоэлектрик | d33(х10-12м/В) | d31(х10-12м/В) |
| ТЦС-4 (жесткая) | -123 | |
| ТЦС-5Н (мягкая) | -274 | |
| ПВДФ | -33 | 2-14 |
Однако низкая плотность, малая диэлектрическая проницаемость и низкий модуль упругости пьезополимеров, и, следовательно, сравнительно высокие значения коэффициентов пьезочувствительности и электромеханической связи, а также легкость формирования из них тонких пленок и хорошая акустическая связь с любой поверхностью делает их эффективными для создания эластичных электромеханических преобразователей сенсорного типа.
Сравнительно высокие электрострикционные свойства полимеров и сополимеров, в том числе блок и привитых сополимеров винилиденфторида с другими сильно полярными мономерами обусловлены содержанием в них полярной кристаллической или стеклообразной аморфной фазы и гибких эластичных цепей, связывающих элементы полярной фазы в единую сетку. Под действием электрического поля элементы полярной фазы ориентируются определенным образом, вызывая натяжение гибких цепей и изменяя размеры образца, Так, при напряжении 20 МВ/м деформация вследствие эффекта электрострикции в таких полимерах достигает 3-4%, С увеличением напряжения до 100 МВ/м деформация возрастает до 11 % вероятнее всего за счет дополнительного эффекта диэлектрической деформации под действием электростатических сил (см. Эффект 1.5). Так как при этом требуется высокое напряжение, лимитирующим фактором получения высокого электромеханического эффекта является электрическая прочность полимеров.
В качестве пьезоэлектриков применяются также полимерные электреты – полярные полимеры со сформированным электрическим моментом за счет замороженной ориентации полярных групп или звеньев (диполей) в результате охлаждения, химических реакций (отверждения) или ориентационной вытяжки в сочетании с воздействием внешнего электрического поля или инжектирования зарядов при облучении потоками заряженных частиц (электронов или ионов). Электреты первой группы обладают разными и разноименными по отношению к электродам зарядами на противоположных сторонах и называются гетероэлектретами, а электреты второй группы – равными и одноименными зарядами и называются гомоэлектретами. В гетероэлектретах диполи ориентированы по всему объему, и исчезновение электретного эффекта обусловлено скоростью дипольной релаксации, резко зависящей от температуры. В гомоэлектретах заряды сосредоточены вблизи поверхности и могут диффундировать в объем или стекать за счет проводимости, поэтому скорость изменения плотности зарядов пропорциональна удельной электропроводности полимера, увеличивающейся с повышением температуры, и напряженности поля электрета.
Наиболее перспективным путем получения пьезоэлектриков, сочетающих свойства полимеров с повышенными пьезоконстантами керамик, является создание полимерных композиционных пьезоэлектрических материалов (ПКПМ), обычно в виде полимерных пленок, содержащих неорганический пьезонаполнитель (пьезопорошок) и подвергнутые воздействию сильного электрического поля в процессе формирования и ориентационной вытяжки композиций при охлаждении. При оценочных расчетах пьезоэлектрических свойств ПКПМ по свойствам компонентов, или фаз - неорганической пьезоэлектрической фазы (наполнителя) с индексом 1 и полимерной фазы с индексом 2 (параметры без индекса относятся к ПКПМ в целом), объемному соотношению фаз (объемным долям φ1 и φ2 соответственно) и характеру их взаимного распределения (фазовой морфологии) в простейших случаях можно воспользоваться тремя типами модельных структур:
· непрерывным полимерным слоем со статистическим распределением сферических частиц пьезопорошка (дисперсной фазы) в слое - матрице (структура матричной дисперсии 0-3, где 0 соответствует нульмерности частиц, а 3 – трехмерности матрицы);
· полимерным слоем с одноосно-ориентированными перпендикулярно плоскости слоя стержнями пьезофазы (последовательная слоистая структура 1-3, где 1 соответствует одномерности стержней, а 3 – трехмерности полимерного слоя);
· полимерным слоем с ориентированными параллельно плоскости слоя стержнями или слоями пьезофазы (параллельная слоистая структура 2-3, где 2 соответствует двумерности слоев, а 3 – трехмерности полимерного слоя).
Для определения электрических свойств таких моделей ПКПМ предполагается, что электрическое поля прилагается перпендикулярно слою (в направлении 33 или zz). Тогда напряженность поля Е и общее электрическое смещение (индукция) D в ПКПМ в соответствие с простым правилом смеси будут равны соответственно: Е=φ1Е1 + φ2Е2 и D=ε0εЕ+Р0= φ1D1+φ2D2, где Р0 – остаточная поляризация, Е1, Е2 и D1, D2 – напряженность поля и индукция в отдельной полимерной и пьезоэлектрической фазах соответственно, причем D1=ε0ε1Е1+Р01, а D2=ε0ε2Е2+Р02. Отношение напряженности поля в частицах пьезонаполнителя и в ПКПМ в целом находят из предположения, что Р0=Р01=Р02=0 и исключения Е2 из получаемого при этом уравнения εЕ=φ1ε1Е1+φ2ε2Е2: 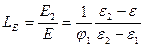 . Для нахождения отношения остаточной поляризации в ПКПМ в целом к остаточной поляризации в частицах пьезонаполнителя предполагается, что остаточная поляризация наблюдается только в наполнителе, т.е. Р02=0, и напряженность внешнего электрического поля в пьезонаполнителе компенсируется внутренним полем, т.е. Е1=0. Тогда Е=Е2 и D1=D2 =D=ε0ε2Е2 , а Р0=ε0 (ε2 – ε) Е, откуда
. Для нахождения отношения остаточной поляризации в ПКПМ в целом к остаточной поляризации в частицах пьезонаполнителя предполагается, что остаточная поляризация наблюдается только в наполнителе, т.е. Р02=0, и напряженность внешнего электрического поля в пьезонаполнителе компенсируется внутренним полем, т.е. Е1=0. Тогда Е=Е2 и D1=D2 =D=ε0ε2Е2 , а Р0=ε0 (ε2 – ε) Е, откуда 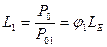 .
.
Аналогичным образом определяются механические упругие свойства ПКПМ по свойствам компонентов и их объемным долям. Обозначим напряжение, относительную деформацию и модуль Юнга при растяжении или сжатии через σ, δ и М соответственно с индексами 1 и 2 для пьезонаполнителя и полимера и без индексов для ПКПМ в целом. При отсутствие остаточных напряжений и использовании простого правила аддитивности: σ=φ1σ1+φ2σ2; δ=φ1δ1+φ2δ2, где σ=Мδ; σ1=М1δ1 ; σ2=М2δ2. Тогда, отношение напряжения в наполнителе к напряжению в ПКПМ в целом и деформации наполнителя к деформации ПКПМ в целом при этом будут равны: 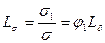 и
и 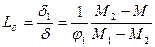 .
.
Выводы обобщенных соотношений между пьезоэлектрическими свойствами наполнителя и ПКПМ с учетом объемной доли и характера распределения частиц или слоев пьезонаполнителя производятся при следующих допущениях:
· внешнее электрическое поле и индукция, механическое напряжение и деформация, остаточная поляризация в ПКПМ в целом и в пьезонаполнителе направлены по оси, перпендикулярной плоскости материала; сжимаемость полимера и наполнителя равна нулю, а механические свойства композита в заданной оси изотропны;
· диэлектрические константы компонентов и ПКПМ в целом не зависят от механических напряжений, а их механические характеристики – от напряженности электрического поля.
В случае прямого пьезоэффекта в ПКПМ протекают три последовательных процесса: деформация δ композита вызывает деформацию пьезонаполнителя δ1, которая в свою очередь приводит к возрастанию его остаточной поляризации Р01 вследствие пьезоэффекта с пьезоконстантой деформации наполнителя е1, а Р01 вызывает увеличение остаточной поляризации Р0 образца в целом. При этом пьезоэлектрическая константа деформации ПКПМ 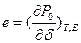 будет равна:
будет равна: 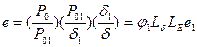 . Обратный пьезоэффект в ПКПМ также обусловлен тремя последовательными процессами: электрическое поле, приложенное к композиту, создает напряженность Е1 в пьезонаполнителе, которая приводит к возрастанию механического напряжения в образце вследствие пьезоэффекта с пьезомодулем наполнителя d1, и, соответственно, к его деформированию. При этом для пьезомодуля ПКПМ
. Обратный пьезоэффект в ПКПМ также обусловлен тремя последовательными процессами: электрическое поле, приложенное к композиту, создает напряженность Е1 в пьезонаполнителе, которая приводит к возрастанию механического напряжения в образце вследствие пьезоэффекта с пьезомодулем наполнителя d1, и, соответственно, к его деформированию. При этом для пьезомодуля ПКПМ 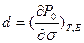 получается следующее выражение:
получается следующее выражение: 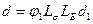 .
.
Для конкретного расчета е и d ПКПМ необходимо знать или рассчитать по свойствам компонентов, их объемным долям и характеру распределения относительную диэлектрическую проницаемость ε и модуль упругости М композита. Для таких расчетов имеется большое количество различных соотношений. В частности, при условии, что относительная диэлектрическая проницаемость и модуль упругости пьезокерамики значительно больше соответствующих значений для полимеров, то для композита в целом со структурой матричной дисперсии (0-3) ε и М можно примерно рассчитать по формулам: 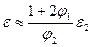 и
и 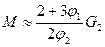 . Тогда расчетные формулы для пьезокоэффициентов е и d ПКПМ имеют вид:
. Тогда расчетные формулы для пьезокоэффициентов е и d ПКПМ имеют вид: 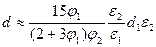 и
и 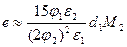 .
.
Для композитов типа 1-3 и 2-3 при таких же условиях все эти формулы существенно упрощаются и имеют вид соответственно: 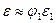 ,
, 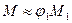 ,
, 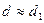 и
и 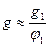 ;
; 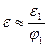 ;
; 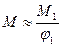 ;
; 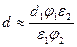 и
и 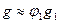 . Из этих соотношений следует, что наибольшей пьезочувствительностью должны обладать композиты типа 1-3, причем коэффициент пьезочувствительности g резко уменьшается при увеличении содержания пьезонаполнителя. ПКПМ тип 0-3 имеют максимальное g при объемной доле пьезонаполнителя порядка 0,6.
. Из этих соотношений следует, что наибольшей пьезочувствительностью должны обладать композиты типа 1-3, причем коэффициент пьезочувствительности g резко уменьшается при увеличении содержания пьезонаполнителя. ПКПМ тип 0-3 имеют максимальное g при объемной доле пьезонаполнителя порядка 0,6.
Дата добавления: 2015-11-26; просмотров: 4772;
