Функция распределения вероятностей случайной величины

Дискретная случайная величина может быть задана перечнем всех её возможных значений и их вероятностей. Такой способ задания не является общим: он не применим, например, для непрерывных случайных величин, так как в этом случае не предоставляется возможным перечислить все возможные значения. Поэтому вводят понятие функции распределения вероятностей случайной величины.

Пусть – действительное число. Вероятность события, состоящего в том, что Х примет значение, меньшее , т.е. вероятность события 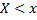, обозначим через .

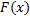Функцией распределения называется функция 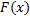, определяющая вероятность того, что случайная величин 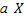в результате испытания примет значение, меньшее , т.е.

.

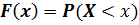Функция распределения обладает следующими свойствами:

1. .

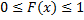2. Если 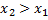, то .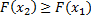

В самом деле, пусть 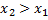. Событие, состоящее в том, что 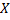примет значение, меньшее 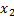, можно подразделить на два несовместных события: 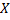примет значение, меньшее 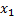и 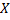примет значение, удовлетворяющее неравенству 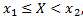т.е. 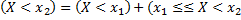). По теореме сложения имеем: 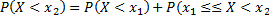), откуда

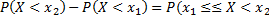) или 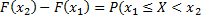. Т.к. любая вероятность есть число неотрицательное, то 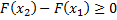или .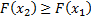

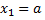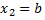Если и , то 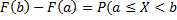. Таким образом, вероятность того, что случайная величина примет значение, заключённое в интервале 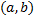, равна приращению функции распределения на этом интервале:

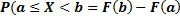
3. Если возможные значения случайной величины принадлежат интервалу 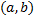, то

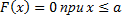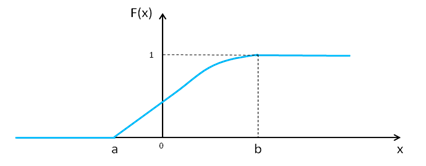
а) , б) 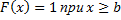. График функции распределения непрерывной случайной величины имеет вид: