Нормальное распределение

Нормальным называется распределение вероятностей непрерывной случайной величины, которое описывается плотностью

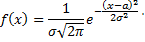
Заметим, что для определения нормального распределения необходимо знать параметры: 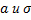. Выясним вероятностный смысл этих параметров. Найдём математическое ожидание непрерывной случайной величины

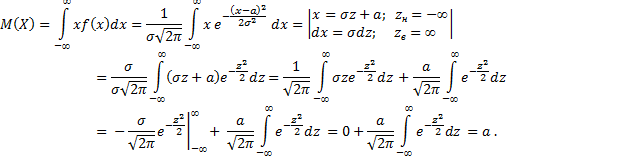
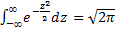- интеграл Пуассона. Итак, математическое ожидание нормального распределения равно параметру 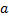, т.е. .

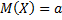Определим дисперсию, учитывая, что .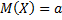

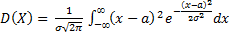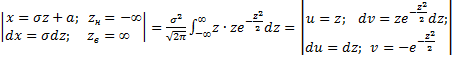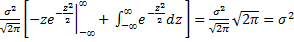= = , т.к. 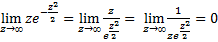. Итак, 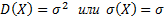. Таким образом второй параметр 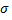равен среднему квадратическому отклонению.

Вычислим вероятность попадания в заданный интервал нормальной случайной величины.

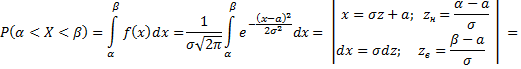
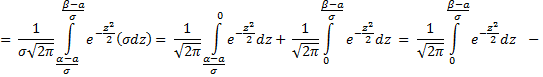
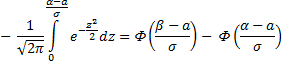
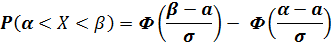
Часто требуется вычислить вероятность того, что отклонение нормально распределённой величины 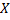по абсолютной величине меньше заданного положительного числа , т.е. требуется найти вероятность осуществления неравенства .

.

.

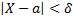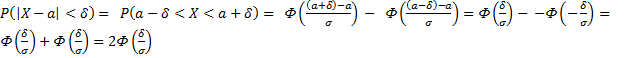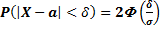Правило трёх сигм

Преобразуем формулу 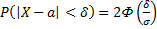, полагая 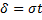. В итоге получим .

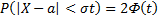Если t=3 и, следовательн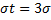о, , то 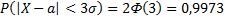, т.е. вероятность того, что отклонение по абсолютной величине будет меньше утроенного среднего квадратического отклонения, равна 0,9973. Другими словами, вероятность того, что абсолютная величина отклонения превысит утроенное среднее квадратическое отклонение, очень мала, а именно равна 0,0027. Это означает, что лишь в 0,27% случаев так может произойти. Такие события практически считаются невозможными. В этом и состоит сущность правила трёх сигм: если случайная величина распределена нормально, то абсолютная величина её отклонения от математического ожидания не превосходит утроенного среднего квадратического отклонения.

На практике правило трёх сигм применяют так: если распределение изучаемой случайной величины неизвестно, но условие, указанное в приведённом правиле, выполняется, то есть основание предполагать, что изучаемая величина распределена нормально; в противном случае она не распределена нормально.