Статистическое распределение выборки. Полигон и гистограмма
Пусть из генеральной совокупности извлечена выборка, причём 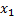 наблюдалось
наблюдалось 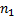 раз,
раз, 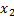 -
- 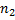 раз, и т.д.
раз, и т.д. 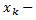
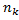 раз и
раз и  - объём выборки.
- объём выборки.
Наблюдаемые значения  называют вариантами, а последовательность вариант, записанных в возрастающем порядке, - вариационным рядом. Числа наблюдений называют частотами, а их отношения к объёму выборки
называют вариантами, а последовательность вариант, записанных в возрастающем порядке, - вариационным рядом. Числа наблюдений называют частотами, а их отношения к объёму выборки 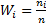 - относительными частотами.
- относительными частотами.
Статистическим распределением выборки называется перечень вариант и соответствующих им частот или относительных частот. Следует отметить, что в теории вероятностей под распределением понимают соответствие между возможными значениями случайной величины и их вероятностями, а в математической статистике – соответствие между наблюдаемыми вариантами и их частотами.
Пусть 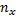 - число наблюдений, при которых наблюдалось значение признака, меньшее
- число наблюдений, при которых наблюдалось значение признака, меньшее 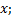
 - объём выборки. Относительная частота события
- объём выборки. Относительная частота события 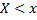 равна
равна 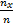 . Если
. Если  изменяется, то, вообще говоря, изменяется и относительная частота, т.е. относительная частота
изменяется, то, вообще говоря, изменяется и относительная частота, т.е. относительная частота 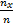 есть функция от
есть функция от  . Так как эта функция находится опытным путём, то её называют эмпирической.
. Так как эта функция находится опытным путём, то её называют эмпирической.
Эмпирической функцией распределения называется функция 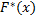 , определяющая для каждого значения
, определяющая для каждого значения  относительную частоту события
относительную частоту события 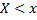 . Итак
. Итак
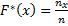 .
.
В отличие от эмпирической функции распределения выборки функцию распределения 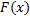 генеральной совокупности называют теоретической функцией распределения. Различие между эмпирической и теоретической функциями состоит в том, что теоретическая функция
генеральной совокупности называют теоретической функцией распределения. Различие между эмпирической и теоретической функциями состоит в том, что теоретическая функция 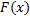 определяет вероятность события
определяет вероятность события 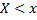 , а эмпирическая функция
, а эмпирическая функция 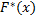 определяет относительную частоту этого же события.
определяет относительную частоту этого же события.
Функция 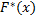 обладает следующими свойствами:
обладает следующими свойствами:
1) значения функции принадлежат отрезку 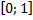 ;
;
2) 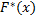 - неубывающая функция;
- неубывающая функция;
3) если 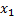 - наименьшая варианта, то
- наименьшая варианта, то 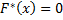 при
при 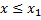 ; если
; если 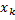 - наибольшая варианта, то
- наибольшая варианта, то 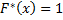 при
при 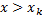 .
.
Пример 1. Найти эмпирическую функцию по данному распределению выборки:
 1 4 6
1 4 6
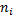 10 15 25
10 15 25
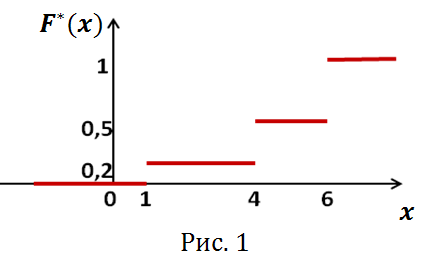 Р е ш е н и е.
Р е ш е н и е. 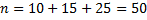 . Наименьшая варианта равна 1, поэтому
. Наименьшая варианта равна 1, поэтому 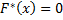 при
при 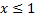 . Значение
. Значение 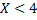 , а именно
, а именно 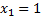 , наблюдалось 10 раз, значит,
, наблюдалось 10 раз, значит, 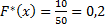 при
при 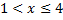 . Значение
. Значение 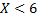 , а именно:
, а именно: 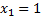 и
и 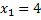 , наблюдалось 10+15=25 раз; следовательно,
, наблюдалось 10+15=25 раз; следовательно,  при
при 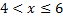 . Так как
. Так как 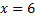 - наибольшая варианта, то
- наибольшая варианта, то 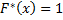 при
при 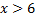 .
.
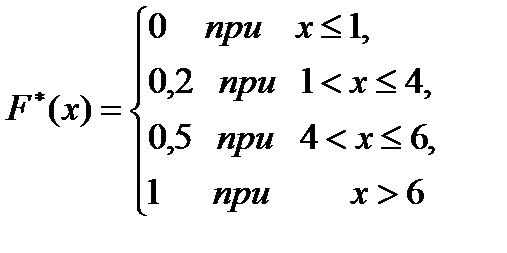
Для наглядности строят различные графики статистического распределения и, в частности, полигон и гистограмму.
 Полигоном частот называют ломаную линию, отрезки которой соединяют
Полигоном частот называют ломаную линию, отрезки которой соединяют
Полигоном относительных частот называют ломаную, отрезки которой соединяют точки 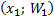 ,
, 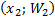 , . . . ,
, . . . , 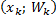 .
.
При непрерывном распределении признака весь интервал, в котором заключены все наблюдаемые значения признака, разбивают на ряд частичных интервалов длиной 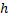 и находят
и находят 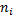 - сумму частот вариант, попавших в i-ый интервал.
- сумму частот вариант, попавших в i-ый интервал.
Гистограммой частот называют ступенчатую фигуру, состоящую из прямоугольников, основаниями которых служат частичные интервалы длины 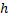 , а высоты равны отношению
, а высоты равны отношению 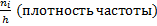 . Площадь частичного -го прямоугольника равна
. Площадь частичного -го прямоугольника равна  - сумме частот вариант, попавших в
- сумме частот вариант, попавших в 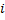 -ый интервал. Площадь гистограммы частот равна сумме всех частот, т.е. объёму выборки
-ый интервал. Площадь гистограммы частот равна сумме всех частот, т.е. объёму выборки  . Гистограммой относительных частот называют ступенчатую фигуру, состоящую из прямоугольников, основаниями которых служат частичные интервалы длиною
. Гистограммой относительных частот называют ступенчатую фигуру, состоящую из прямоугольников, основаниями которых служат частичные интервалы длиною 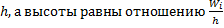 (плотность относительной частоты).
(плотность относительной частоты).
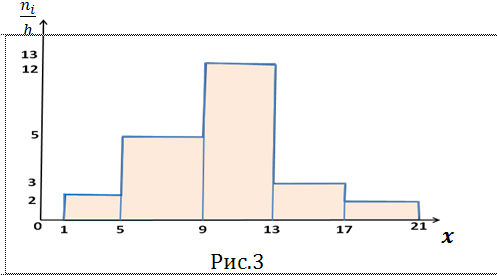 На рис. 3 изображена гистограмма частот по данному распределению выборки объёма
На рис. 3 изображена гистограмма частот по данному распределению выборки объёма 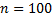 .
.
Частичный интервал
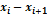
| Сумма частот
вариант интервала
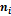
| Плотность
частоты
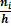
|
| 1 – 5 | 2,5 | |
| 5 – 9 | ||
| 9 – 13 | 12,5 | |
| 13 – 17 | ||
| 17 – 21 |
Дата добавления: 2015-12-29; просмотров: 1961;
