Оценка генеральной дисперсии по исправленной выборочной
Пусть из генеральной совокупности в результате  независимых наблюдений над количественным признаком
независимых наблюдений над количественным признаком 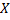 извлечена повторная выборка объёма
извлечена повторная выборка объёма  :
:

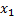
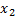 …
… 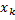
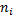
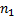
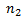 …
… 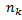
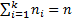
Требуется по данным выборки оценить неизвестную генеральную дисперсию  . Если в качестве оценки генеральной дисперсии принять выборочную дисперсию, то эта оценка будет приводить к систематическим ошибкам, давая заниженное значение генеральной дисперсии. Объясняется это тем, что выборочная дисперсия является смещённой оценкой
. Если в качестве оценки генеральной дисперсии принять выборочную дисперсию, то эта оценка будет приводить к систематическим ошибкам, давая заниженное значение генеральной дисперсии. Объясняется это тем, что выборочная дисперсия является смещённой оценкой  , другими словами, математическое ожидание выборочной дисперсии не равно оцениваемой генеральной дисперсии, а равно
, другими словами, математическое ожидание выборочной дисперсии не равно оцениваемой генеральной дисперсии, а равно
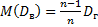 .
.
Легко «исправить» выборочную дисперсию так, чтобы её математическое ожидание было равно генеральной дисперсии. Достаточно для этого умножить 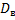 на дробь
на дробь 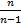 , после чего получим исправленную дисперсию, которую обозначают через
, после чего получим исправленную дисперсию, которую обозначают через 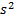 :
:
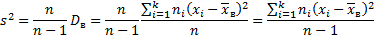
Исправленная дисперсия является, конечно, несмещённой оценкой генеральной дисперсии, а именно:
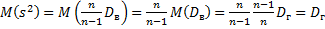 .
.
Итак, в качестве оценки генеральной дисперсии принимают исправленную дисперсию
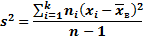
Дата добавления: 2015-12-29; просмотров: 1503;
