Метод произведений для вычисления выборочных средней и дисперсии
Метод произведений даёт удобный способ вычисления условных моментов различных порядков вариационного ряда с равноотстоящими вариантами. Зная условные моменты, можно найти начальные и центральные эмпирические моменты. Методом произведений удобно вычислять выборочную среднюю и выборочную дисперсию. Покажем применение этого метода на конкретном примере.
Пример 3. Найти методом произведений выборочную среднюю и выборочную дисперсию по заданному распределению выборки объёма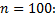 
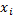12 14 16 18 20 22
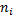5 15 50 16 10 4
Составим расчётную таблицу
| 
| 
| 
| 
| 
|
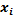
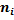
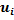
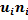
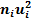
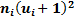
| -2 | -10 | ||||
| -1 | -15 | ||||
| 
| 
| 
|
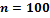
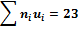
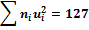
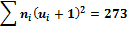
Для контроля вычислений пользуются тождеством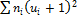 
= 
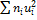+2 
+ 
.
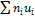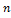К о н т р о л ь :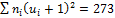 
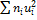+2 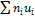+ 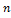=127+2 
23+100=273
Совпадение контрольных сумм свидетельствует о правильности вычислений.
Вычислим условные моменты первого и второго порядков:
.
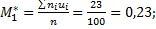
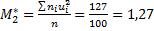Найдём шаг: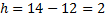 
. В нашем случае ложный нуль 
.
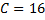Вычислим выборочные среднюю и дисперсию:
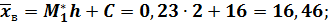
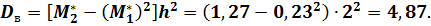
Сведение первоначальных вариант к равноотстоящим
Рассмотренный метод был применим для равноотстоящих вариант. Однако на практике, как правило, данные наблюдений не являются равноотстоящими числами. Поэтому предварительно вариационный ряд приводят к равноотстоящим. Для этого интервал, в котором заключены все наблюдаемые значения признака (первоначальные варианты), делят на несколько равных частичных интервалов. Практически в каждый частичный интервал должно попасть не менее 8 – 10 первоначальных вариант. Затем находят середины частичных интервалов, которые и образуют последовательность равноотстоящих вариант. В качестве частоты каждой «новой» варианты (середины частичного интервала) принимают общее число первоначальных вариант, попавших в соответствующий частичный интервал.
Дата добавления: 2015-12-29; просмотров: 3156;