Элементы теории корреляции
Изучение разнообразных явлений сопровождается выяснением закономерностей, которым подчиняются характерные для данных явлений количественные соотношения или связи. При этом оказывается, что только для тех явлений, происхождение которых связывается с чётко учтёнными факторами, количественные соотношения или связи имеют вполне точный и определённый характер. В этом случае говорят, что количественные соотношения или связи связаны функциональной зависимостью. Строгая функциональная зависимость реализуется редко, так как изменение одного показателя определяется не только изменением другого основного показателя, но и влиянием ряда сопутствующих второстепенных факторов. Так, при установлении взаимосвязи между показателями использования основных средств и уровня производительности труда на заводе выясняется, что на уровень производительности труда, помимо объёма затрачиваемых основных средств, влияют ещё и другие факторы - рационализация производственного процесса, организация труда и др. В отличие от функциональной зависимости связь такого характера между двумя величинами называется статистической.
Статистической называют зависимость, при которой изменение одной из величин влечёт изменение распределения другой.
Степень рассеяния возможных значений 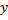 , соответствующих каждому значению
, соответствующих каждому значению  , характеризует большую или меньшую тесноту связи между этими величинами. Это значит, что если влияние неучтённых факторов на изучаемую связь между величинами
, характеризует большую или меньшую тесноту связи между этими величинами. Это значит, что если влияние неучтённых факторов на изучаемую связь между величинами  и
и 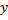 незначительно, то степень рассеяния значений
незначительно, то степень рассеяния значений 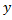 мала, а связь между
мала, а связь между  и
и 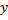 имеет большую тесноту.
имеет большую тесноту.
В частности, статистическая зависимость проявляется в том, что при изменении одной из величин изменяется среднее значение другой. В этом случае статистическую зависимость называют корреляционной. Например, с одинаковых по площади участков земли при равных количествах внесённых удобрений снимают различный урожай. Это объясняется влиянием случайных факторов – осадки, температура воздуха и др. Вместе с тем, как показывает опыт, средний урожай является функцией от количества удобрений, т.е. эти признаки связаны корреляционной зависимостью.
Результаты эксперимента, данные наблюдений или измерений дают совокупность значений между переменными величинами в виде таблицы. Требуется выразить эту зависимость между переменными аналитически, т.е. в виде формулы. Такая формула очень облегчает анализ изучаемой зависимости. Формулы, служащие для аналитического представления опытных данных, принято называть эмпирическими формулами. Во многих случаях характер зависимости между переменными величинами предполагается известным из каких-либо теоретических соображений и задача подбора эмпирической формулы сводится к тому, чтобы определить числовые значения параметров, входящих в формулу данного вида.
Чаще всего при подборе эмпирических формул пользуются так называемым принципом наименьших квадратов. Он основан на том, что из данного множества формул вида 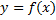 наилучшим образом изображающей данные значения считается та, для которой сумма квадратов отклонений наблюдаемых значений от вычисленных является наименьшей. Подбор параметров функции
наилучшим образом изображающей данные значения считается та, для которой сумма квадратов отклонений наблюдаемых значений от вычисленных является наименьшей. Подбор параметров функции 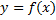 , основанный на этом принципе, называется способом наименьших квадратов.
, основанный на этом принципе, называется способом наименьших квадратов.
Необходимо помнить, что способ наименьших квадратов применяется для подбора параметров после того, как вид функции 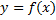 определён. Если из теоретических соображений нельзя сделать никаких выводов о том, какой должна быть эмпирическая формула, то приходится руководствоваться наглядными представлениями, прежде всего графическим изображением наблюдаемых данных. Вид функции
определён. Если из теоретических соображений нельзя сделать никаких выводов о том, какой должна быть эмпирическая формула, то приходится руководствоваться наглядными представлениями, прежде всего графическим изображением наблюдаемых данных. Вид функции 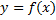 выбирается таким образом, чтобы график этой функции по возможности близко напоминал расположение на графике данных наблюдений.
выбирается таким образом, чтобы график этой функции по возможности близко напоминал расположение на графике данных наблюдений.
Покажем, как практически подбираются по способу наименьших квадратов коэффициенты для функции простейшего вида 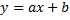 . Пусть изучается система количественных признаков
. Пусть изучается система количественных признаков 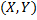 . В результате
. В результате  независимых опытов получены
независимых опытов получены  пар чисел
пар чисел 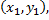
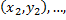
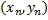 . Найдём по данным наблюдений выборочное уравнение прямой линии регрессии
. Найдём по данным наблюдений выборочное уравнение прямой линии регрессии 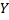 на
на 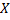 :
: 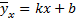 .Поскольку различные значения
.Поскольку различные значения  признака
признака 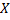 и соответствующие им значения
и соответствующие им значения 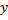 признака
признака 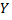 наблюдались по одному разу, то группировать данные нет необходимости и нет надобности использовать понятие условной средней, поэтому искомое уравнение можно записать так:
наблюдались по одному разу, то группировать данные нет необходимости и нет надобности использовать понятие условной средней, поэтому искомое уравнение можно записать так:
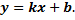
Угловой коэффициент прямой линии регрессии 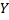 на
на 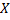 называют выборочным коэффициентом регрессии
называют выборочным коэффициентом регрессии 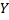 на
на 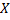 и обозначают через
и обозначают через 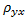 .
.
Итак, будем искать выборочное уравнение прямой линии регрессии 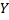 на
на 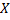 вида
вида
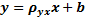 . (1)
. (1)
Подберём параметры 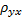 и
и 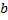 так, чтобы точки
так, чтобы точки 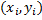 ,
, 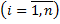 построенные по данным наблюдений, на плоскости
построенные по данным наблюдений, на плоскости 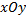 лежали как можно ближе к прямой (1). Уточним смысл этого требования. Назовём отклонением разность
лежали как можно ближе к прямой (1). Уточним смысл этого требования. Назовём отклонением разность 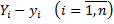 , где
, где 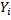 - вычисленная по уравнению (1) ордината, соответствующая наблюдаемому значению
- вычисленная по уравнению (1) ордината, соответствующая наблюдаемому значению  ;
; 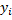 - наблюдаемая ордината, соответствующая
- наблюдаемая ордината, соответствующая  .
.
Подберём параметры 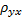 и
и 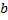 так, чтобы сумма квадратов отклонений была минимальной. Так как каждое отклонение зависит от отыскиваемых параметров, то и сумма квадратов отклонений есть функция этих параметров
так, чтобы сумма квадратов отклонений была минимальной. Так как каждое отклонение зависит от отыскиваемых параметров, то и сумма квадратов отклонений есть функция этих параметров
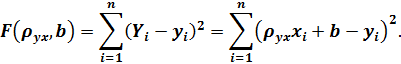
Для отыскания минимума приравняем нулю соответствующие частные производные:
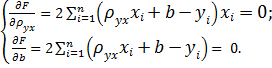 (2)
(2)
Выполнив элементарные преобразования, получим систему двух линейных уравнений относительно 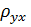 и
и 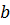 :
:
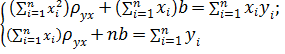 (3)
(3)
Решив эту систему, найдём искомые параметры:
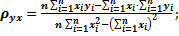 (4)
(4)
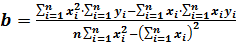 . (5)
. (5)
Корреляционная таблица
При большом числе наблюдений одно и то же значение  может встретиться
может встретиться 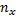 раз, одно и то же значение
раз, одно и то же значение 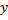 -
- 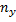 раз, одна и та же пара чисел
раз, одна и та же пара чисел 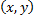 может наблюдаться
может наблюдаться 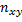 раз. Поэтому данные наблюдений группируют, т.е. подсчитывают частоты
раз. Поэтому данные наблюдений группируют, т.е. подсчитывают частоты 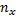 ,
, 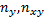 . Все сгруппированные данные записывают в виде таблицы, которая называется корреляционной.
. Все сгруппированные данные записывают в виде таблицы, которая называется корреляционной.
| Y | X | 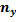
| |||
| 0,4 | - | ||||
| 0,6 | - | ||||
| 0,8 | - | - | |||
| 
|
Дата добавления: 2015-12-29; просмотров: 891;
