Методика вычисления выборочного коэффициента корреляции
Найти выборочное уравнение прямой линии регрессии Y на X по данным, приведённым в корреляционной табл.1.
Таблица 1
| Y | X | 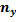
| ||||
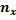
| 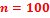
|
При определении выборочного уравнения прямой линии регрессии основная задача сводится к определению 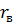 . Для упрощения расчётов на практике переходят к условным вариантам
. Для упрощения расчётов на практике переходят к условным вариантам 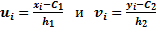 .
.
Составим корреляционную табл. 2 в условных вариантах, выбрав в качестве ложных нулей 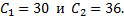
Таблица 2
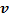
| 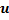
| 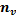
| ||||
| -2 | -1 | |||||
| -2 | ||||||
| -1 | ||||||
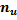
| 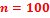
|
В этом случае выборочный коэффициент корреляции вычисляют по формуле (при этом величина 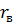 не изменится)
не изменится)
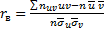 .
.
Величины 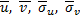 можно найти методом произведений или вычислить непосредственно исходя из определений этих величин:
можно найти методом произведений или вычислить непосредственно исходя из определений этих величин:
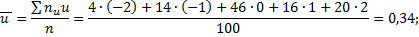
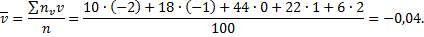
Для определения 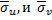 найдём предварительно
найдём предварительно 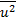 и
и 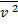 :
:
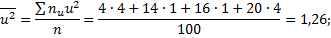
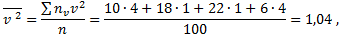
тогда 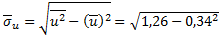 =1,07;
=1,07; 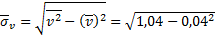 =1,02.
=1,02.
Остаётся указать способ вычисления 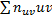 , где
, где 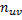 - частота пары условных вариант
- частота пары условных вариант 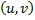 . Можно доказать, что справедливы формулы:
. Можно доказать, что справедливы формулы:
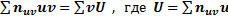 ,
,
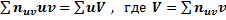 .
.
Для контроля целесообразно выполнить расчёты по обеим формулам и сравнить результаты; их совпадение свидетельствует о правильности вычислений.
Для вычисления 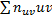 составим расчётную табл. 3.
составим расчётную табл. 3.
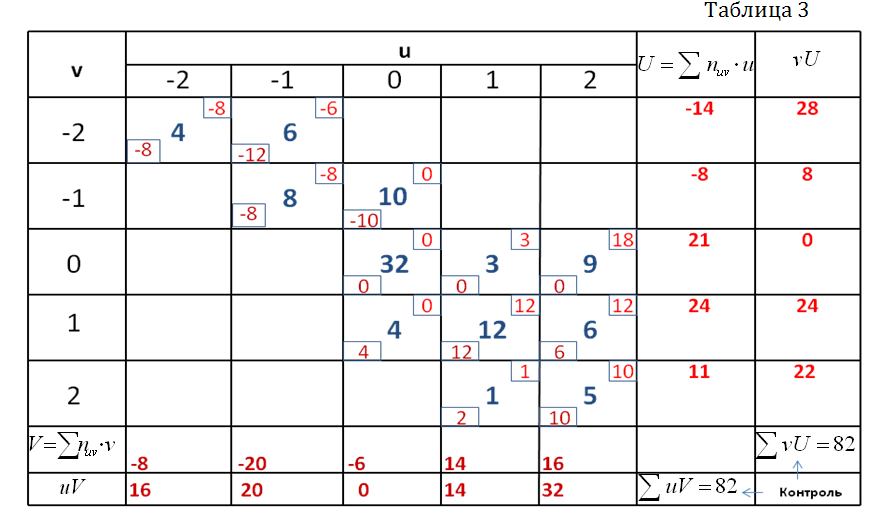
Пояснения к составлению табл.3:
В каждой клетке, в которой частота 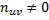 , записывают в правом верхнем углу произведение частоты
, записывают в правом верхнем углу произведение частоты 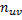 на варианту
на варианту 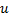 . Например, в правых верхних углах клеток первой строки записаны произведения: 4
. Например, в правых верхних углах клеток первой строки записаны произведения: 4 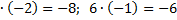 .
.
Складывают все числа, помещённые в правых верхних углах клеток одной строки и их сумму записывают в клетку этой же строки столба 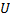 . Например, для первой строки
. Например, для первой строки 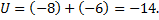
Умножают варианту 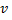 на
на 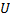 и полученное произведение записывают в последнюю клетку той же строки
и полученное произведение записывают в последнюю клетку той же строки 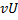 . Например, в первой строке таблицы
. Например, в первой строке таблицы 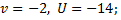 следовательно
следовательно 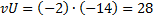 .
.
Сложив все числа столбца 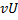 , получают сумму
, получают сумму 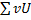 , которая равна искомой сумме
, которая равна искомой сумме 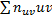 . Например, в нашем случае
. Например, в нашем случае 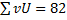 , следовательно
, следовательно 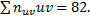
Для контроля аналогичные вычисления производят по столбцам: произведения 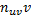 записывают в левый нижний угол клетки, содержащей частоту
записывают в левый нижний угол клетки, содержащей частоту 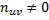 ; все числа, помещённые в левых нижних углах клеток одного столбца, складывают и их сумму записывают в строке V; далее умножают каждую варианту
; все числа, помещённые в левых нижних углах клеток одного столбца, складывают и их сумму записывают в строке V; далее умножают каждую варианту 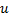 на V и результат записывают в клетках последней строки.
на V и результат записывают в клетках последней строки.
Сложив все числа последней строки, получают сумму 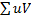 , которая также равна
, которая также равна 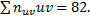
Найдём выборочный коэффициент корреляции:
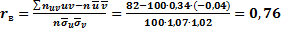 .
.
Найдём шаги 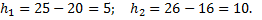
Найдём 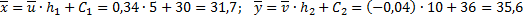
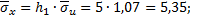
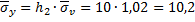 .
.
Подставив найденные величины в уравнение 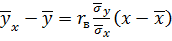 , получим искомое уравнение прямой линии регрессии Y на X:
, получим искомое уравнение прямой линии регрессии Y на X:
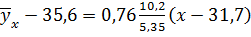 или
или
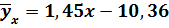 .
.
Дата добавления: 2015-12-29; просмотров: 1309;
