Стандартная (каноническая) форма задачи линейного программирования

В практических задачах формы линейных условий, определяющих многогранник решений ЗЛП, могут быть очень разнообразны. Часть условий может быть задана в виде равенств, причем на некоторые переменные могут не налагаться требования неотрицательности. Это затрудняет исследование ЗЛП и главное – требует разработки специальных методов для решения каждого варианта задачи. Поэтому возникает необходимость ввести понятие стандартной формы ЗЛП.

При стандартной форме линейной модели

а) все ограничения записываются в виде равенств с неотрицательной правой частью;

б) значения всех переменных модели неотрицательны;

в) целевая функция подлежит максимизации или минимизации.

Покажем, каким образом любую линейную модель можно привести к стандартной.

Ограничения

1. Исходное ограничение, записанное в виде неравенства типа 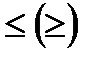, можно представить в виде равенства, прибавляя остаточнуюпеременную к левой части ограничения (вычитаяизбыточнуюпеременную из левой части).

Например, в левую часть исходного ограничения 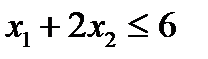вводится остаточная переменная 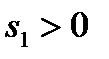, в результате чего исходное неравенство обращается в равенство .

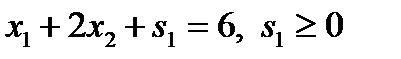2. Рассмотрим исходное ограничение другого типа: 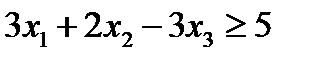. Для обращения исходного неравенства в равенство, вычтем из его левой части избыточную переменную 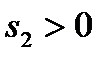. В результате получим .

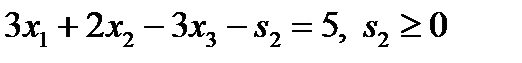3. Правую часть равенства всегда можно сделать неотрицательной, умножая обе части на -1. Например, неравенство 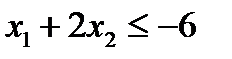заменить .

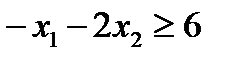Переменные

Любую переменную 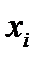, не имеющую ограничения в знаке, можно представить как разность двух неотрицательных переменных: .

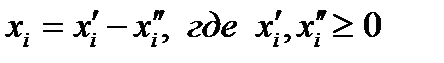Целевая функция

Целевая функция линейной оптимизационной модели, представленной в стандартной форме, может подлежать как максимизации, так и минимизации. В некоторых случаях оказывается полезным изменить исходную целевую функцию. Максимизация некоторой функции эквивалентна минимизации той же функции, взятой с противоположным знаком, и наоборот. Например, максимизация функции 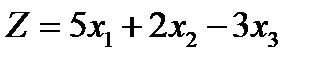эквивалентна минимизации функции 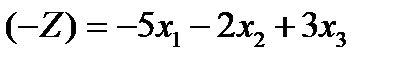. Эквивалентность означает, что при одной и той же совокупности ограничений оптимальные значения переменных 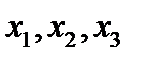в обоих случаях будут одинаковы. Отличие заключается только в том, что при одинаковых числовых значениях целевых функций их знаки будут противоположны.