Построение математической модели
Процесс построения математической модели для решения поставленной задачи можно начать с ответов на три следующие вопроса:
1. Для определения каких величин должна быть построена модель? Другими словами, надо ввести переменные для решения задачи.
2. Какие ограничения должны быть наложены на переменные, чтобы выполнялись условия, характерные для моделируемой системы?
3. В чем состоит цель, для достижения которой из всех допустимых значений переменных нужно выбрать те, которые будут соответствовать оптимальному решению задачи?
| Исходный продукт | Расход исходных продуктов (в тоннах) на тонну краски | Максимально возможный запас, т | |
| Краска Н | Краска В | ||
| А | |||
| С |
Задача 1. Фабрика изготовляет два вида красок: для внутренних (В) и наружных (Н) работ. Продукция обоих видов поступает в оптовую продажу. Для производства красок используются два исходных продукта – А и С. Максимально возможные суточные запасы этих продуктов составляют 6 и 8 т соответственно. Расходы А и С на 1 т соответствующих красок приведены в таблице. Изучение рынка сбыта показало, что суточный спрос на краску (В) никогда не превышает спроса на краске (Н) более чем на 1 т. Кроме того, установлено, что спрос на краску (В) никогда не превышает 2 т в сутки. Оптовые цены одной тонны красок равны: 3 тыс. руб. для краски (Н), 2 тыс. руб. для краски (В). Какое количество краски каждого вида должна производить фабрика, чтобы доход от реализации продукции был максимальным?
Переменные:
Целевая функция:
Ограничения: 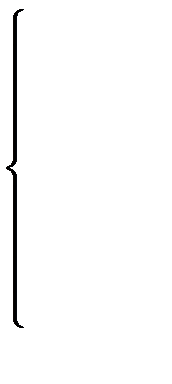
Неявное ограничение заключается в том, что объёмы производства продукции не могут принимать отрицательных значений. Чтобы предотвратить получение таких недопустимых решений, потребуем выполнения условия неотрицательности переменных, т.е. введем ограничения на их знак:
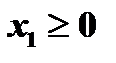 (объём производства краски (Н)),
(объём производства краски (Н)),
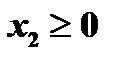 (объём производства краски (В)).
(объём производства краски (В)).
Математическая модель данной задачи будет иметь вид:
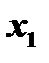 - суточный объём производства краски (Н)
- суточный объём производства краски (Н)
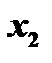 - суточный объём производства краски (В)
- суточный объём производства краски (В)
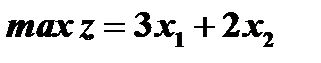
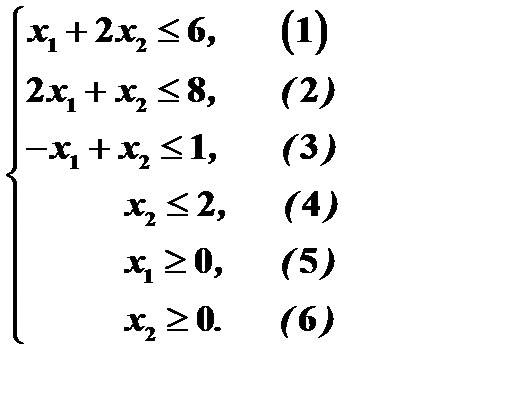
Презентация построения математической модели задачи 1
Дата добавления: 2015-12-29; просмотров: 869;
