Задача о назначениях

Требуется распределить 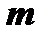работ по 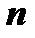станкам. Работа 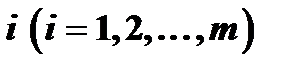, выполнимая на станке 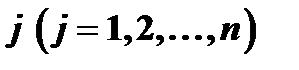, связана с затратами 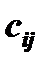. Задача состоит в таком распределении работ по станкам ( одна работа выполняется одним станком ), которое соответствует минимуму суммарных затрат. Такая задача известна как задача о назначениях.

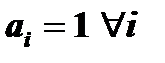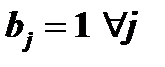Эту задачу можно рассматривать как частный случай транспортной задачи. Здесь работы представляют «исходные пункты», а станки – «пункты назначения». Предложение в каждом исходном пункте равно 1, т.е. . Аналогично спрос в каждом пункте назначения равен 1, т.е. . Стоимость «перевозки» (прикрепления) работы 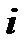к станку 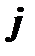равна 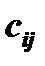. Если какую-либо работу нельзя выполнить на некотором станке, то соответствующая стоимость 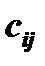берётся равной очень большому числу .

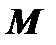Общая структура задачи о назначениях имеет вид:

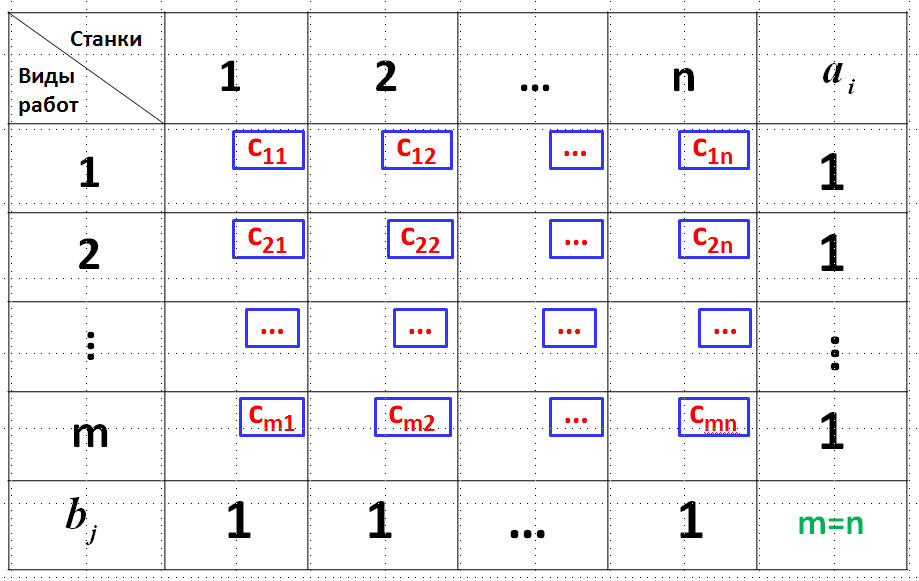
В случае существования дисбаланса, добавив фиктивные работы или станки в зависимости от начальных условий, можно его ликвидировать. Поэтому без потери общности можно положить .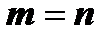

Задачу о назначениях можно представить следующим образом. Пусть

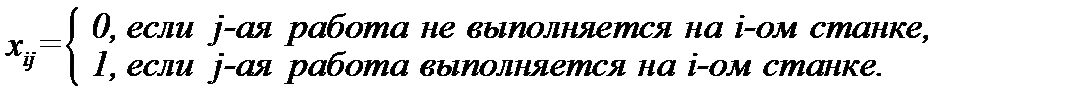
Теперь задача будет формулироваться как

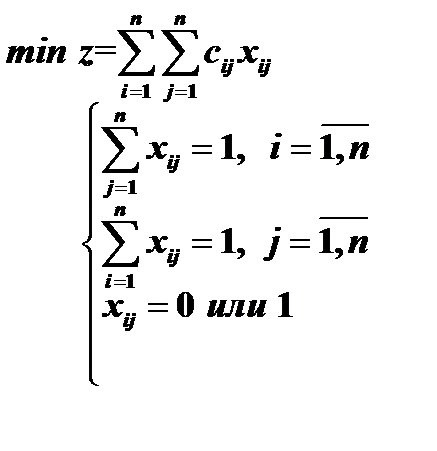
Заметим, что оптимальное решение задачи о назначениях не изменится, если к любой строке или столбцу матрицы стоимостей прибавить (или вычесть) постоянную величину. В самом деле, есл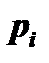и и 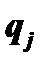вычитаются из 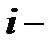ой строки и 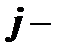го столбца, то новые стоимости имеют вид 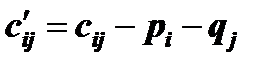. Отсюда получается новая целевая функция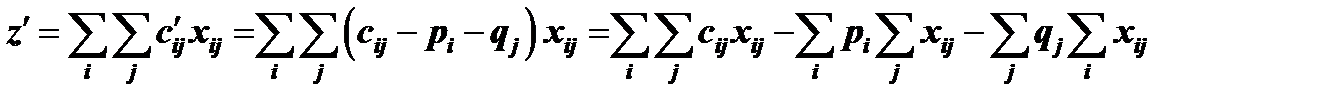

Поскольку 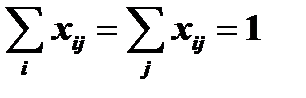, то 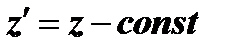. Следовательно, минимизация исходной целевой функции 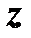приводит к такому же решению, как минимизация 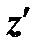. Приведённое соображение показывает, что если можно построить новую 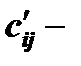матрицу с нулевыми элементами и эти нулевые элементы соответствуют допустимому решению, то такое решение будет оптимальным, поскольку стоимость не может быть отрицательной.

Специфическая структура задачи о назначениях позволяет разработать эффективный метод её решения. Покажем, как реализуется этот метод на примере.