Вероятностные эффекты в потоковых динамических задачах
При изменении интенсивности входного потока и переброске пропускной способности может меняться загрузка некоторых каналов. При этом будет изменяться очередь в ожидании обслуживания единиц потока, которые
рассматриваются в модели. МОДУС предназначен для отображения макроструктурной динамики, где критическими точками являются моменты перехода системы в другой структурно-функциональный режим. Динамика оперативного характера (задержка конкретного поезда, мгновенное состояние очереди и т.п.) отражается потом в контрольной имитационной модели. В модели, построенной на базе МОДУС, необходимо уловить динамику средней очереди Μ04(φ(t)) в зависимости от изменения загрузки ψ(t) канала. МОДУС — аппарат детерминированного моделирования, однако динамические свойства модели позволяют отображать главные вероятностные эффекты.
Рассмотрим элементарную часть системы, в которой проявляются вероятностные эффекты — некоторый канал и перед ним бункер. Несовпадения колебания ритмов поступления заявок и ритмов обслуживания приводит к возникновению очереди, средняя величина которой зависит от разброса колебаний прибытия, обслуживания и коэффициента загрузки.
Изменения пропускной способности существенно влияет лишь на
последний параметр ψ(t) (здесь t отображает макродинамику). Среднее время (при данной структуре системы) простоя вагонов в очереди t04(φ) зависит от
Моч(ф) и от загрузки канала φ(t). Вагоночасы простоя,
которые должны учитываться при оценке структурно-функционального режима, равны
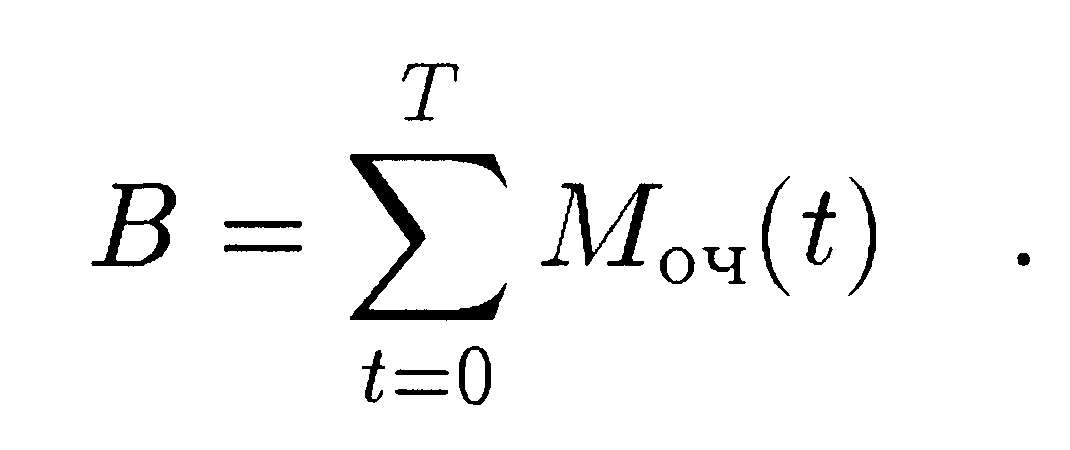
Для отображения изменения вагоночасов простоя в очереди при изменении загрузки канала предлагается структурный блок – сетевой бункер.
На выбор структуры сети и структуры потоков во времени будут влиять два фактора — величина средней очереди и среднее время простоя в очереди. Эти факторы, в свою очередь, зависят от загрузки системы, которая изменяется при изменении интенсивности входного потока или в случае переброски пропускной способности. Изменение загрузки системы при заданной стоимости простоя вызывает изменение значения функционала.
Оптимизация работы транспортной системы по натуральным показателям.
1. Способы сведения некоторых критериев системы к одному («свертка» критериев).
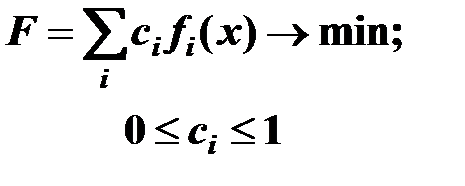
где 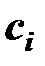 - весовой коэффициент;
- весовой коэффициент;
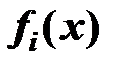 - показатель работы системы.
- показатель работы системы.
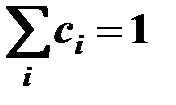 .
.
Данный способ возможен, когда показатели идентичны, т.е. имеют одну основу, например, стоимостную.
Для транспортной системы такой способ представляется малопригодным.
2. Оптимизация производства по одному из критериев, все остальные переводятся в ограничения.
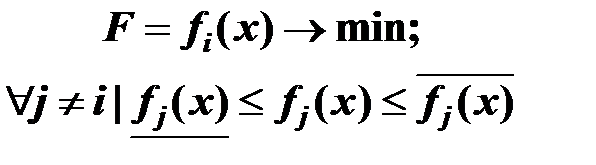
Различные стороны функционирования транспортной системы отображаются в разных показателях. Например, диспетчеру необходимо одновременно следить за своевременной подачей порожних и груженых вагонов на предприятия с соблюдением графика формирования составов, выполнением оборота вагонов и т.д. Недостаточная изученность экономического содержания показателей не позволяет легко сопоставить положительный эффект от улучшения одних и ущерб от ухудшения других.
Практический опыт позволяет обычно определить наилучшие значения каждого показателя в данной ситуации. В подавляющем большинстве случаев при отклонении значения параметра от оптимальной величины затраты возрастают не линейно. Оптимизация заключается в минимизации отклонения параметров от номинальных значений, причем отклонения берутся квадратично, чтобы отобразить нелинейность затрат.
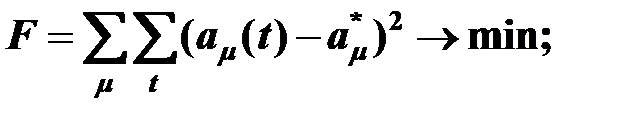
где 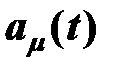 - текущее значение параметра;
- текущее значение параметра;
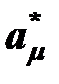 - номинальное или наилучшее значение параметра.
- номинальное или наилучшее значение параметра.
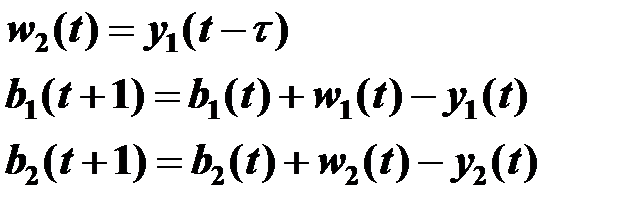
Классы задач, которые можно решать данным методом
1). Минимизация оборота вагонов.
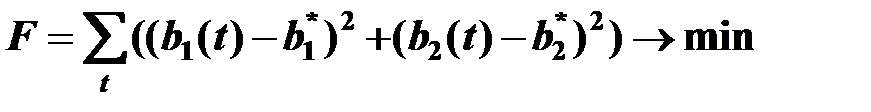
Для каждой станции существует такое рациональное заполнение вагонами, когда она работает наиболее эффективно – хорошо идет процесс накопления, загружены локомотивы, обеспечивается пропуск поездов и т.д. Такое значения и выбираются в качестве номинальных 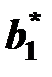 и
и 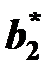 .
.
2). Обеспечение ритмичной подачи вагонов предприятиям.

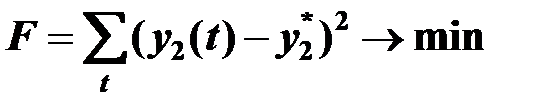
3). Обеспечение выполнения плана погрузки-выгрузки.
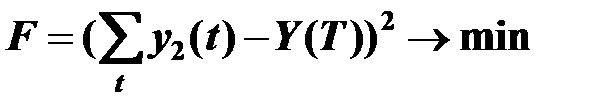
где Y(T) – план погрузки-выгрузки за период Т.
Ставится задача одновременно обеспечить выполнение плана погрузки-выгрузки, ритмичного снабжения вагонами предприятий и минимизации оборота вагонов в системе.
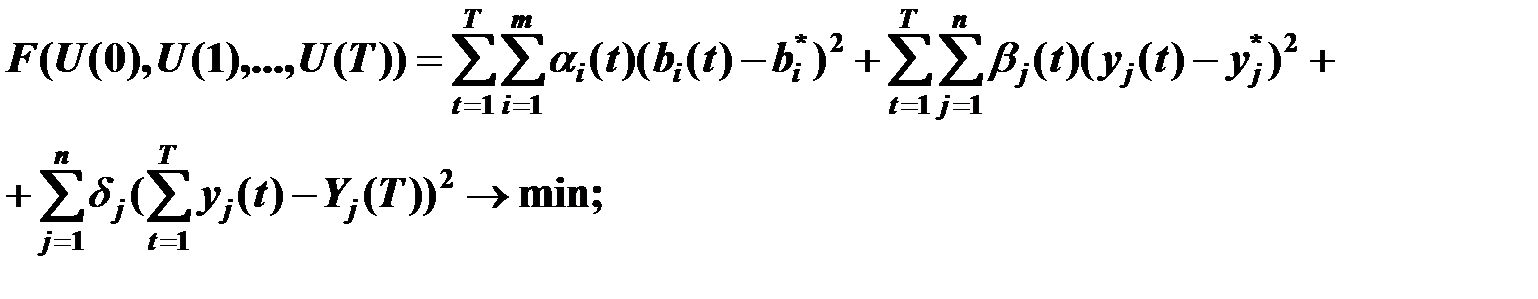
где m – количество бункеров;
n – количество выходных потоков в системе;
Т – период оптимизации;
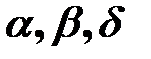 - весовые коэффициенты.
- весовые коэффициенты.
Весовые коэффициенты играют роль своеобразного управления. Проводя последовательный направленный перебор весовых коэффициентов, можно обеспечить удовлетворения всех параметров.
Чем выше значение весового коэффициента, тем труднее поддерживать в системе значение соответствующего параметра в требуемых пределах. Это, с другой стороны, позволяет судить об узких местах в технологии работы исследуемой системы.
Краткий алгоритм решения задачи.
На 1 этапе состояние бункеров в каждый момент времени 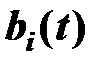 выражаются через состояние бункеров в 0-й момент времени, суммы входящих и выходящих потоков.
выражаются через состояние бункеров в 0-й момент времени, суммы входящих и выходящих потоков.
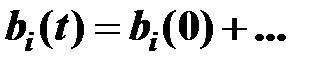
На 2 этапе берутся частные производные 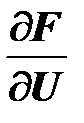 , вследствие чего получается система (Т+1) линейных уравнений с (Т+1) неизвестными.
, вследствие чего получается система (Т+1) линейных уравнений с (Т+1) неизвестными.
На 3 этапе решается система (Т+1) уравнений методами решения задач линейного программирования.
Дата добавления: 2015-12-22; просмотров: 1221;
