Анализ динамических рядов
Динамический рядпредставляет собой хронологическую последовательность числовых значений статистических показателей.
Виды рядов динамики (РД):
1) моментные (моментальные) РД;
2) интервальные РД;
3) РД с нарастающими итогами;
4) производные РД.
Моментные ряды динамики отображают состояние изучаемых явлений на определенные даты (моменты) времени. Особенностью моментного ряда динамики является то, что в его уровни могут входить одни и те же единицы изучаемой совокупности. Пример моментного ряда динамики:
| Дата | 1.01.2001 | 1.04.2001 | 1.07.2001 | 1.10.2001 | 1.01.2002 |
| Число работников, чел. |
Интервальные ряды динамики отображают итоги развития (функционирования) изучаемых явлений за отдельные периоды (интервалы) времени. Каждый уровень интервального ряда складывается из данных за более короткие интервалы. Пример интервального ряда динамики:
| Год | |||||
| Объем розничного товарооборота, тыс. руб. | 885,7 | 932,6 | 980,1 | 1028,7 | 1088,4 |
Статистическое отображение развития изучаемого явления во времени может быть представлено рядами динамики с нарастающими итогами. Их применение обусловлено потребностями в результатах развития изучаемых показателей не только за данный отчетный период, но и с учетом предшествующих периодов. При составлении таких рядов производится последовательное суммирование смежных уровней. Этим достигается суммарное обобщение результата развития изучаемого показателя с начала отчетного периода (месяца, квартала, года и т.д.).
Производные ряды – ряды, уровни которых представляют собой не непосредственно наблюдаемые значения, а производные величины: средние или относительные.
Основные направления изучения закономерностей развития социально-экономических явлений с помощью рядов динамики:
- характеристика уровней развития изучаемых явлений во времени;
- измерение динамики изучаемых явлений посредством системы статистических показателей;
- выявление и количественная оценка основной тенденции развития (тренда);
- изучение периодических колебаний;
- экстраполяция и прогнозирование.
Таблица 8.1 Уровни (показатели) ряда динамики
| Показатель | Формула | |
| Базисные | Абсолютный прирост | Δ 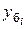 = yi – у0 (6.1) = yi – у0 (6.1)
|
| Темп роста | 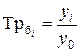 (6.2) (6.2)
| |
| Темп прироста | 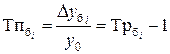 (6.3) (6.3)
| |
| Цепные | Абсолютный прирост | Δ 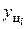 = yi – yi-1 (6.4) = yi – yi-1 (6.4)
|
| Темп роста | 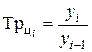 (6.5) (6.5)
| |
| Темп прироста | 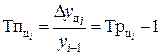 (6.6) (6.6)
| |
| Темп наращивания | 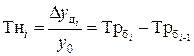 (6.7) (6.7)
| |
| Абсолютное значение 1% прироста | 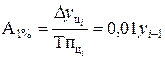 (6.8) (6.8)
| |
| Средние | Абсолютный прирост | 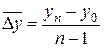 = = 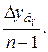 (6.9) (6.9)
|
| Темп роста | 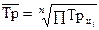  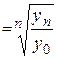 (6.10) (6.10)
| |
| Темп прироста | 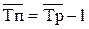 (6.11) (6.11)
|
Средний уровень ряда динамики характеризует типическую величину абсолютных уровней.
Средний уровень интервального ряда определяется по формуле средней арифметической простой:
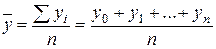 , (6.12)
, (6.12)
где n – число уровней.
В моментном ряду динамики с равностоящими датами средний уровень определяется по формуле средней хронологической простой:
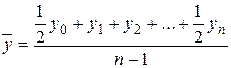 . (6.13)
. (6.13)
В моментном ряду динамики с неравноотстоящими датами средний уровень определяется по формуле средней хронологической взвешенной:
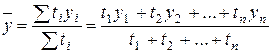 , (6.14)
, (6.14)
где уi – уровни ряда динамики, сохранившиеся без изменения в течение промежутка времени ti.
Между базисными и цепными темпами роста имеется взаимосвязь: произведение последовательных цепных темпов роста равно базисному темпу роста, а частное от деления последующего базисного темпа роста на предыдущий равно соответствующему цепному темпу роста.
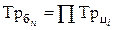 ;
; 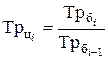 . (6.15)
. (6.15)
Дата добавления: 2015-11-28; просмотров: 1731;
