Регрессионный анализ. Для оценки параметров уравнений регрессии наиболее часто используется метод наименьших квадратов (МНК)

Для оценки параметров уравнений регрессии наиболее часто используется метод наименьших квадратов (МНК), суть которого заключается в следующем требовании: искомые теоретические значения результативного признака 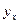должны быть такими, при которых бы обеспечивалась минимальная сумма квадратов их отклонений от эмпирических (фактических) значений, т.е.

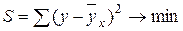. (5.1)

При изучении связей показателей применяются различного вида уравнения прямолинейной и криволинейной связи. Так, при анализе прямолинейной зависимости применяется уравнение:

(5.2)

Это наиболее часто используемая форма связи между коррелируемыми признаками, при парной корреляции она выражается уравнением (6.2), где а₀ – среднее значение в точке x=0, поэтому экономической интерпретации коэффициента нет; а₁ – коэффициент регрессии, показывает, на сколько изменяется в среднем значение результативного признака при увеличении факторного на единицу собственного измерения.

При криволинейной зависимости применяется ряд математических функций:

полулогарифмическая 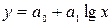(5.3)

показательная 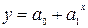(5.4)

степенная 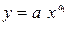(5.5)

параболическая 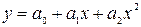(5.6)

гиперболическая 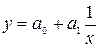(5.7)

Система нормальных уравнений МНК для линейной парной регрессии имеет следующий вид:

(5.8)

Отсюда можно выразить коэффициенты регрессии:

;

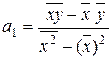. (5.9)

При численности объектов анализа до 30 единиц возникает необходимость проверить, насколько вычисленные параметры типичны для отображаемого комплекса условий, не являются ли полученные значения параметров результатом действия случайных причин. Значимость коэффициентов регрессии применительно к совокупности n<30 определяется с помощью t-критерия Стьюдента. При этом вычисляются фактические значения t-критерия:

для параметра а₀: 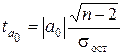, (5.10)

для параметра а₁: . (5.11)

В формулах (6.10) и (6.11):

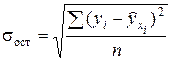– среднее квадратическое отклонение результативного признака от выровненных значений 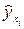. (5.12)

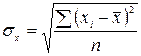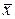– среднее квадратическое отклонение факторного признака от общей средней . (5.13)

Полученные по формулам (5.10) и (5.11) фактические значения и 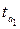сравниваются с критическим 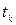, который получают по таблице Стьюдента с учетом принятого уровня значимости 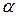и числа степеней свободы ν(ν=n-k-1, где n – число наблюдений, k – число факторов, включенных в уравнение регрессии). Рассчитанные параметры а₀ и а₁ уравнения регрессии признаются типичными, если t фактическое больше t критического.

На практике часто приходится исследовать зависимость результативного признака от нескольких факторных признаков. Аналитическая форма связи результативного признака от ряда факторных признаков выражается и называется многофакторным (множественным) уравнением регрессии.

Линейное уравнение множественной регрессии

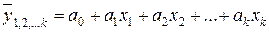. (5.14)

Система нормальных линейных уравнений МНК для оценки коэффициентов двухфакторной регрессии 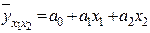имеет вид:

(5.15)