Закон больших чисел и предельные теоремы
Под законом больших чисел в широком смысле понимается общий принцип, согласно которому, по формулировке академика Колмогорова, совокупное действие большого числа случайных факторов приводит к результату, почти не зависящему от случая. Или иначе: При большом числе случайных величин их средней результат перестает быть случайным и может быть предсказан с большой степенью определенности.
Под законом больших чисел в узком смысле понимается ряд математических теорем, в каждой из которых для тех или иных условий устанавливается факт приближения средних характеристик большого числа испытаний к некоторым определенным постоянным.
Неравенство Чебышева: для любой случайной величины, имеющей математическое ожидание M(X) и дисперсию D(X) справедливо:
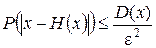 ,(4.1)
,(4.1)
или
 ,(4.2)
,(4.2)
Если формула (6.1) устанавливает верхнюю границу рассматриваемого события, то (4.2) – нижнюю границу вероятности события, состоящего в том, что отклонения значения случайной величины от математического ожидания не превысит (не будет менее) величины  , где
, где 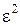 – достаточно малая величина.
– достаточно малая величина.
В приложении к выборочному методу неравенство Чебышева может быть сформулировано так: при неограниченном увеличении числа наблюдений ( 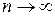 ) в генеральной совокупности с ограниченной дисперсией с вероятностью близкой к единице можно ожидать, что отклонение выборочной средней (
) в генеральной совокупности с ограниченной дисперсией с вероятностью близкой к единице можно ожидать, что отклонение выборочной средней ( 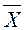 ) от генеральной средней
) от генеральной средней 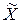 будет сколь угодно мало:
будет сколь угодно мало: 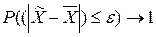 при
при 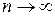 . Эту вероятность в теореме А.М. Ляпунова (1901г.) используют для определения ошибки наблюдений.
. Эту вероятность в теореме А.М. Ляпунова (1901г.) используют для определения ошибки наблюдений.
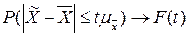 , (4.3)
, (4.3)
где  - нормированная формула Лапласса.
- нормированная формула Лапласса.
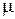 – средняя квадратическая или стандартная ошибка выборки.
– средняя квадратическая или стандартная ошибка выборки.
 . (4.4)
. (4.4)
Пусть надо измерить некоторою величину, истинное значение которой равно a. Пусть результат каждого измерения – случайная величина Xi(i=1,2,…,n). Если при измерениях отсутствует систематические погрешности, то M(Xi)=a при любом i. Тогда средняя арифметическая результатов и измерений сходится по вероятности к истинному значению a.
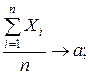 (4.5)
(4.5)
Дисперсия средней случайной величины Xi равна
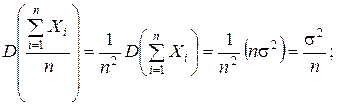 (4.6)
(4.6)
Среднее квадратическое отклонение ошибок выборки
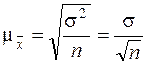 , (4.7)
, (4.7)
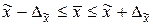 . (4.8).
. (4.8).
Зная выборочную среднюю 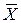 и предельную ошибку выборки
и предельную ошибку выборки 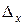 можно определить границы, в которых размещена генеральная средняя
можно определить границы, в которых размещена генеральная средняя 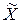 .
.
Величина средней квадратической ошибки простой случайной повторной выборки может быть определена по формуле:
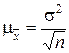 , (4.9)
, (4.9)
т.е. чем больше вариация признака в генеральной совокупности, тем больше ошибка выборки.
Величину 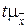 называют предельной ошибкой для определения значения вероятности. Если требуется оценить среднюю генеральной совокупности
называют предельной ошибкой для определения значения вероятности. Если требуется оценить среднюю генеральной совокупности 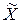 с вероятностью 0,9545, то надо получить значение выборочной средней из соотношения
с вероятностью 0,9545, то надо получить значение выборочной средней из соотношения 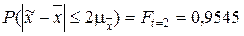 (функция Лапласа).
(функция Лапласа).
Для выборки объема  предельная ошибка
предельная ошибка 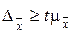 может быть определена из соотношения
может быть определена из соотношения 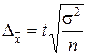 .
.
| t | 1,00 | 1,96 | 2,00 | 2,58 | 3,00 |
| F(t) | 0,683 | 0,9500 | 0,9545 | 0,9901 | 0,9973 |
 – это предел возможной ошибки (правило «трех сигм»).
– это предел возможной ошибки (правило «трех сигм»).
Формула предельной ошибки выборки используется не только для оценки пределов, в которых находится изучаемый признак в генеральной совокупности, но и для определения необходимого объема выборки при заданной ее ошибке. Третий тип задач, которые могут быть решены с использованием предельной ошибки выборки, – это определение вероятности, с которой можно гарантировать, что ошибка выборки не выйдет за заданные пределы.
Величина дисперсии генеральной совокупности  принципиально не известна и можно говорить лишь о ее оценке по результатам одной выборки.
принципиально не известна и можно говорить лишь о ее оценке по результатам одной выборки.
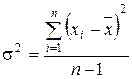 –для простой случайной выборки.
–для простой случайной выборки.
При 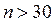 , поправка
, поправка 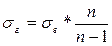 становится
становится 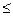 3,5% (30/(30-1)), поэтому ею можно пренебречь.
3,5% (30/(30-1)), поэтому ею можно пренебречь.
Дата добавления: 2015-11-28; просмотров: 1112;
