Адаптивные модели сезонных явлений

Несмотря на гибкость, с которой адаптивные модели временных рядов отражают изменения в характере динамики прогнозируемых показателей, однако возможности их применения ограничены. Прежде всего, это касается процессов, характеризующихся периодически повторяющимися сезонными эффектами. Для прогнозирования таких процессов разработан специальный класс моделей, отличительной особенностью которых является наличие в их структуре коэффициентов сезонности. В зависимости от способа включения этого коэффициента различают два типа этих моделей.

К первому типу относятся модели с мультипликативным коэффициентом сезонности

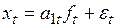, (6. 13)

где 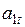– изменяющийся во времени коэффициент, динамика которого характеризует тенденцию развития процесса;

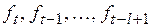– коэффициенты сезонности;

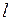– количество фаз в полном сезонном цикле (при месячных наблюдениях 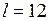, при квартальных – ).

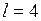Ко второму типу относятся модели с аддитивным коэффициентом сезонности

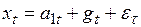, (6.14)

где 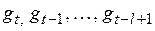– адаптивные коэффициенты сезонности.

Фактически модели этих типов представляют собой определенного рода комбинацию адаптивного полинома нулевой степени и соответствующего коэффициента сезонности. Если моделируемый процесс имеет тенденцию линейного роста, то в моделях (6.13), (6.14) член, соответствующий полиному нулевого порядка, заменяется полиномом первого порядка, и тогда модели записываются в следующем виде:

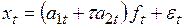, (6.15)

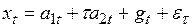. (6.16)

Расчет текущих оценок коэффициентов всех этих моделей осуществляется с использованием принципа экспоненциального сглаживания. Так, например, расчет прогнозного значения 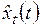с помощью мультипликативной модели осуществляется по рекуррентной схеме

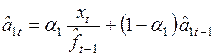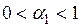, , (6.17)

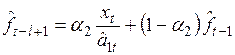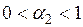, , (6.18)

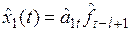. (6.19)

Величина 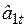определяется как взвешенная сумма текущего значения 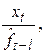полученного путем исключения сезонных колебаний из фактических данных 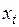и предшествующей оценки 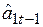. В этом случае в качестве коэффициента сезонности 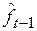берется его наиболее поздняя оценка, сделанная для аналогичной фазы цикла. Полученная по первому уравнению величина 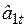используется впоследствии для определения новой оценки коэффициента сезонности во втором уравнении.

Для сезонной модели, учитывающей тенденцию линейного роста, можно записать аналогичную рекуррентную схему

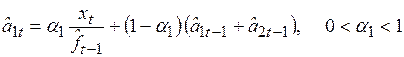, (6.20)

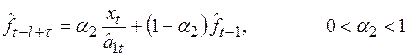, (6.21)

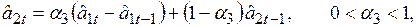(6.22)

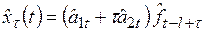. (6.23)

Добавление коэффициента 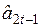несколько изменило расчетные формулы предыдущей схемы, но принцип их построения остался прежним: во всех формулах используется процедура экспоненциального сглаживания. Прогнозные значения, рассчитанные с помощью рекуррентной схемы (6.20)–(6.23), также как и с помощью (6.17)–(6.19), представляют собой некую функцию прошлых и текущих данных, параметров 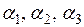и первоначальных значений 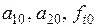. Точность прогноза зависит от начальных значений и параметров адаптации. Поэтому ниже специально будет рассмотрен вопрос о проблемах их оптимизации.

Существует интересное обобщение, учитывающее возможность построения сезонных моделей путем комбинирования различных типов тенденций с коэффициентами сезонности мультипликативного и аддитивного видов. В зависимости от характера динамики моделируемого процесса рекомендуется выбирать одну из девяти моделей, объединенных в три группы.

Первая группа включает модели, отражающие:

1) отсутствие закономерностей роста (модель без тренда)

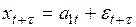; (6.24)

2) тенденцию линейного роста (модель с аддитивным линейным трендом)

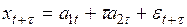; (6.25)

3) тенденцию экспоненциального роста (модель с мультипликативным трендом)

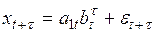. (6.26)

Во второй класс входят модели, получаемые из первого путем включения в их структуру аддитивных коэффициентов сезонности. Это включение трансформирует (6.24) – (6.26) в модели следующего вида:

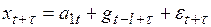, (6.27)

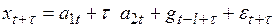, (6.28)

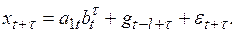(6.29)

Третий класс, в отличие от второго, в своей структуре содержит не аддитивный, а мультипликативный коэффициент сезонности

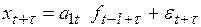, (6.30)

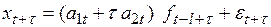, (6.31)

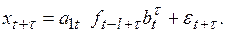(6.32)

Для каждой из этих моделей оценка параметра 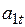осуществляется по формуле

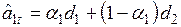, (6.33)

где 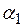– параметр сглаживания ;

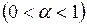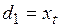– для моделей первой группы;

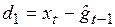– для моделей второй группы;

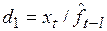– для моделей третьей группы;

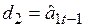– для моделей, не отражающих рост;

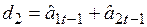– для моделей, отражающих тенденцию линейного роста;

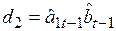– для моделей, отражающих тенденцию экспоненциального роста.

В свою очередь, оценка коэффициентов линейного роста 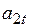осуществляется с помощью выражения

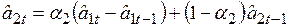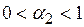, , (6.34)

а коэффициентов экспоненциального роста 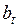по формуле

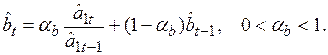(6.35)

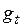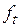Оценки коэффициентов сезонности и рассчитываются по формулам

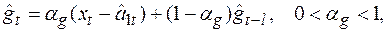(6.36)

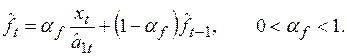(6.37)

Такое комбинирование позволяет строить адаптивные модели с целенаправленно выбранным набором свойств. Правильно выбранные свойства, гарантируя требуемую адекватность модели, обеспечивают тем самым повышение достоверности прогнозных расчетов. Однако автоматический выбор, например, в процессе настройки параметров адаптации, в рассматриваемой схеме не предусмотрен. Поэтому для выбора нужного типа модели в каждом конкретном случае требуется проведение дополнительных исследований по предварительному выяснению основных свойств прогнозируемых процессов или применение специальных процедур сравнения по формальным критериям и определения в некотором смысле «лучшей» прогнозной модели.

[1] Дуброва Т.М. Статистические методы прогнозирования: Учеб. пособие для вузов / Т.А. Дуброва. – М.: ЮНИТИ-ДАНА, 2003. – С. 116.