Адаптивные многошаговые модели

В моделях предыдущего параграфа используется одношаговый (по одному наблюдению) принцип обработки вновь поступающей информации. Это приводит к чрезмерному влиянию последнего наблюдения на формирование величины прогнозного значения. Как показывает опыт, эффект последнего наблюдения негативно (снижается уровень точности) проявляется в тех случаях, когда упреждение прогнозных расчетов 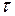превосходит единицу. Этот нежелательный факт объясняется тем, что в каждом отдельном наблюдении текущего момента, по которому осуществляется корректировка модели, доля полезной информации о будущем по мере роста упреждающего периода снижается. Любые усложнения адаптивного механизма хотя и могут привести к некоторому снижению этого эффекта, но полного решения этой проблемы обеспечить не могут. Очевидно, что одношаговый принцип является ограничивающим фактором в расширении круга прогнозных задач, решаемых в рамках адаптивного подхода. В связи с этим возникает необходимость рассмотрения моделей, в которых используются другие принципы обработки вновь поступающих наблюдений. Разумный шаг в решении этой проблемы заключается в том, чтобы построить алгоритмы, позволяющие для корректировки коэффициентов модели на каждом шаге использовать вместо одного несколько наблюдений.

Алгоритмы, в которых для корректировки коэффициентов модели используется более одного наблюдения, как отмечалось в предыдущем параграфе, в отличие от одношаговых, принято называть многошаговыми. Термин «многошаговый» может не совсем точно отражает суть обсуждаемой процедуры, так как на самом деле в одном шаге многошаговой процедуры одновременно реализуется несколько шагов одношаговой. И если многошаговый РМНК позволяет получить тот же самый результат, что и многократное применение процедуры одношагового РМНК, то для адаптивных моделей, что станет понятно из данного параграфа, это совсем не так.

Сначала познакомимся с особенностями построения адаптивной прогнозной модели на основе многошаговой рекуррентной схемы оценивания. В качестве базовой, будем использовать многошаговую рекуррентную схему МНК. Варианты конкретной реализации этой схемы могут отличаться с одной стороны количеством вновь поступающих на обработку наблюдений, а с другой – способом формирования этих наблюдений в группу, которая принимается за порцию одновременно обрабатываемой информации. Ситуации, когда порция состояла всего из одного наблюдения, были уже рассмотрены ранее, теперь нас будут интересовать порции из нескольких наблюдений. Учитывая, что в реальных ситуациях обновление динамических рядов, как правило, осуществляется периодическим добавлением одного наблюдения (годового, квартального, месячного и т.п.) построим вычислительную процедуру многошагового адаптивного алгоритма с использованием способа формирования порции из группы наблюдений по принципу скользящей замены. Обычно этот принцип применяют в процедуре вычисления скользящего среднего. Согласно этому принципу вновь поступившее наблюдение добавляется в конец группы, а хронологически самое раннее исключается из нее, т.е. группа из последовательности наблюдений 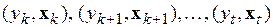заменяется соответственно на 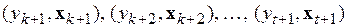. Такой способ формирования порции особенно удобен тогда, когда для получения прогнозных оценок используются короткие временные ряды. Число наблюдений в группе одновременно обрабатываемых может быть произвольным, но, как правило, его стремятся выбирать, исходя из объема выборки, периода упреждения и, как станет ясно из дальнейшего изложения, в зависимости от получаемой точности прогнозных расчетов.

Для случая, когда вектор поправок определяется по группе из 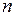наблюдений, сформированной по вышеописанному принципу, экстремальная задача вычисления оценок вектора коэффициентов модели с использованием экспоненциально взвешенного квадратичного критерия может быть записана следующим образом:

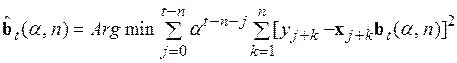. (5.55)

Как и в базовой задаче, здесь минимизируется экспоненциально взвешенная сумма квадратов отклонений, но в отличие от базовой, одно и то же значение весового коэффициента одновременно приписывается 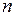различным отклонениям. Фактически взвешивается не отдельно каждое наблюдение, а сразу вся группа одновременно обрабатываемых наблюдений. Правда, если вспомнить принцип формирования такой группы, то станет ясно, что не все наблюдения одной и той же группы должны иметь равные весовые коэффициенты.

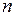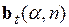Изменение размера группы (величины ) приводит к соответствующему перераспределению весовых коэффициентов между отдельными наблюдениями. А это значит, что коэффициенты регрессионной модели зависят еще от одного параметра, принимающего значения натурального ряда . Чтобы подчеркнуть это обстоятельство, в записи коэффициента присутствует параметр 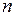, который также как и параметр 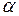можно настраивать

Дифференцирование функционала задачи (5.55) по 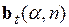приводит для получения оценок 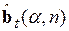к следующей системе уравнений:

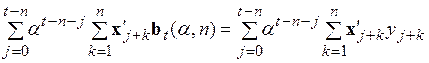. (5.56)

Если использовать весовую функцию (5.56), матрица весов которой, например, для случая 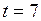, , 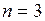имеет вид

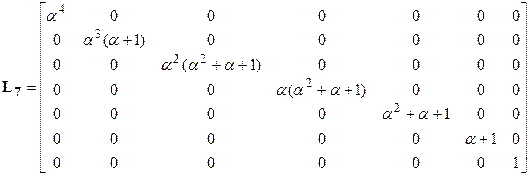
то систему (5.56) можно записать в более компактной матричной форме

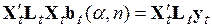. (5.57)

Разрешая систему (5.57) относительно 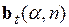, получаем выражение для вычисления оценки вектора коэффициентов

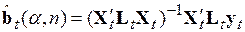. (5.58)

Чтобы (5.58) превратить в рекуррентную формулу для вычисления тех же самых оценок 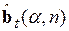, будем считать, что после того, как была рассчитана 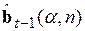, поступило 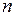новых наблюдений, в качестве которых рассматриваются последние наблюдения, известные к моменту 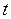. Основываясь на этом предположении, запишем систему (5.58) в виде

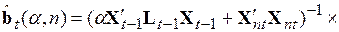
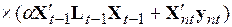, (5.59)

где первая круглая скобка представляет собой обратную матрицу суммы двух матриц, первая из которых есть матрица системы нормальных уравнений, полученной для 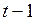наблюдения, а вторая – для 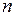последних; аналогично вторая круглая скобка представляет сумму соответствующих слагаемых правой части этой системы.

Используя обозначение

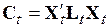
и рекуррентную формулу обращения матриц, преобразуем систему к следующему виду:

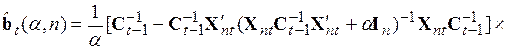
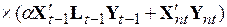. (5.60)

Затем, проведя почленное перемножение, можно записать выражение

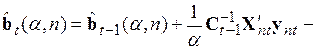
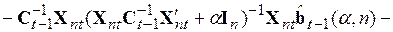
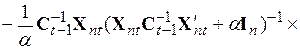
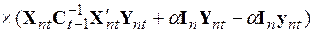, (5.61)

в котором к последнему сомножителю прибавили и отняли одну и ту же величину 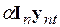. Вынесем в последнем сомножителе 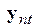за скобку и после почленного перемножения и перегруппировки запишем

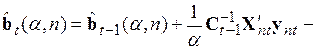
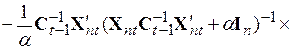
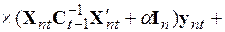
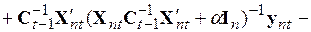
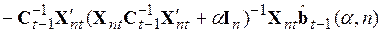. (5.62)

Перемножение матриц в третьем члене позволяет осуществить взаимное уничтожение второго и третьего члена в полученном выражении, а вынесение общего множителя из последних двух членов приводит к рекуррентной формуле

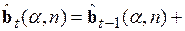
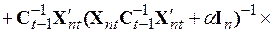
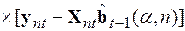, (5.63)

где 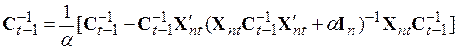. (5.64)

Полученные рекуррентные формулы позволяют записать многофакторную модель с многошаговым адаптивным механизмом в следующем виде:

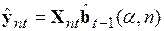, (5.65)

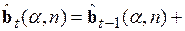
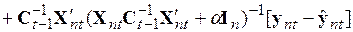, (5.66)

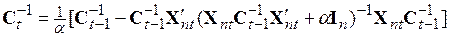. (5.67)