Эта запись получена с использованием тригонометрического тождества

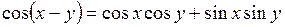. (6.4)

Обычно временной ряд представляет собой сумму многих периодических рядов. Согласно одной из самых распространенных моделей стационарный временной ряд представляет собой бесконечную сумму периодических рядов

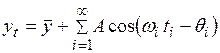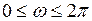, (7.5)

или

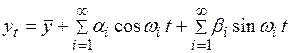. (7.6)

Теоретически можно показать, что любой стационарный временной ряд может быть с любой точностью аппроксимирован бесконечным рядом синусоид и косинусоид. Такое представление называют рядом Фурье. Разработан мощный математический аппарат исследования этих рядов. Однако временные ряды в экономике слишком коротки, чтобы можно было использовать этот аппарат. Поэтому рассматриваются другие модели.

Аддитивная и мультипликативная модели

Временного ряда

Построение аддитивной и мультипликативной моделей (6.1), (6.2) сводится к расчету значений трендовой ( 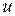), сезонной ( 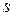), случайной ( 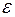) компонент для каждого уровня ряда и предполагает выполнение следующих шагов:

1. Выравнивание исходного ряда методом скользящей средней.

2. Расчет значений сезонной компоненты .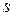

3. Устранение сезонной компоненты из исходных уровней ряда и получение выравненных данных ( 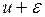) в аддитивной или ( 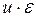) в мультипликативной модели.

4. Аналитическое выравнивание уровней ( 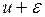) или ( 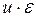) и расчет значений 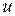с использованием полученного уравнение тренда.

5. Расчет полученных по модели значений ( 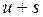) или ( ).

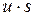6. Расчет абсолютных и/или относительных ошибок.