Агрегатные индексы. Построение взаимосвязанных агрегатных индексов

Общие индексы по форме построения могут быть агрегатными и средними.

Агрегатные индексы – это индексы, в которых числитель и знаменатель представляют собой сумму произведений показателей (т.е. агрегат). Как правило, перемножаются два показателя: один из них – индексируемая величина, а второй – ее вес.

Агрегатная форма индекса является основной, наиболее распространенной формой индекса в экономических исследованиях.

Агрегатный способ построения индексов позволяет с помощью определенных соизмерителей получить итоговое (суммарное) значение несопоставимых единиц сложной совокупности и в последующем сопоставить эти суммы в отчетном и базисном периодах (см. пример, таблица 9.1).

Наиболее типичные представители агрегатных индексов – индексы физического объема и цен, а также индекс стоимости. В тех случаях, когда имеются данные о производстве (о продаже) различных несоизмеримых в физических единицах продуктов в одной и той же совокупности за 2 периода и необходимо охарактеризовать изменение всего объема продуктов, они с помощью определенных соизмерителей (цены, себестоимости, трудоёмкости и т.п.) выражаются в одинаковых единицах измерения: например, q*p, q*z, q*t, и т.д. Это дает возможность соизмерить объемы продуктов в отчетном и базисном периодах:

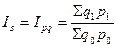агрегатный индекс стоимости, (9.9)

который показывает относительное изменение стоимости продуктов как за счет изменения цен, так и за счет изменения объема продуктов.

Абсолютное изменение стоимости продуктов может быть оценено как

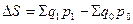. (9.10)

Индекс стоимости показывает, что изменение индексируемой величины обусловлено воздействием двух факторов: физического объема и цен. Для того, чтобы выявить влияние каждого из них, рассчитываются так называемые факторные индексы, которые по форме построения также являются агрегатными.

Агрегатный индекс физического объема получают путем сопоставления стоимости продукции отчетного и базисного периодов, исчисленной в неизменных ценах: ценах базисного периода:

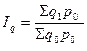, (9.11)

где 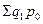– стоимость продукции отчетного периода в базисных ценах;

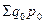– стоимость продукции базисного периода.

Вычитая из числителя знаменатель, можно определить на сколько в абсолютном выражении изменилась стоимость продукции за счет изменения физического объема:

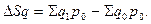(9.12)

По аналогии строится и агрегатный индекс цен. Только в данном случае индексируемая величина – p, а веса – физические объемы, т.е. .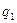

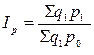, (9.13)

где 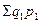– стоимость продукции отчетного периода;

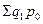– стоимость продукции отчетного периода в базисных ценах.

Изменение стоимости продукции за счет изменения цен в абсолютном выражении:

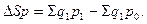(9.14)

В нашем примере (таблица 9.1):

Общее изменение товарооборота:

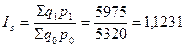(+12,31%)

или в абсолютном выражении:

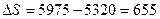тыс. р.

В т.ч.

1) за счет изменения количества проданных товаров:

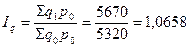(+6,58%)

или в абсолютном выражении:

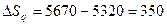тыс. р.

2) за счет изменения цен:

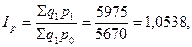
что в абсолютном выражении составит:

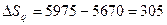тыс.р.

Вывод. Товарооборот в июне увеличился по сравнению с предыдущим месяцем на 12,31 %, или на 655 тыс. р. Это увеличение вызвано воздействием двух факторов: за счет роста физического объема проданных товаров – на 6,58 % (350 тыс. р.) и за счет роста цен – на 5,38 % (305 тыс. р.)

Взаимосвязь индексов 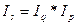носит название сопряженности индексов.

Построение системы взаимосвязанных индексов требует соблюдения следующих правил:

- веса сопряженных (факторных) индексов должны быть зафиксированы в факторных индексах на разных уровнях;

- при построении агрегатных индексов количественных величин веса (цены, себестоимость) фиксируются на базисном уровне;

- при построении агрегатных индексов качественных величин веса (физический объем) фиксируется на уровне отчетного периода.

Так, например, агрегатный индекс общих издержек:

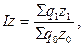(9.15)

в т.ч. 1) за счет физического объема:

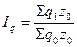; (9.16)

2) за счет себестоимости единицы продукции:

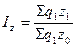. (9.17)

Тогда 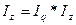– сопряженные индексы.

Свойство сопряженности используется:

а) для проверки правильности расчетов;

б) для нахождения неизвестного индекса по остальным известным, с которыми он связан как сопряженный. Например:

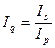или .

Однако на практике индексы цен и индексы физического объема могут рассчитываться и по-иному. У этого факта есть исторический аспект.

Впервые агрегатная форма индекса была предложена немецким ученым Э.Ласпейресом для измерения цен на товары. В качестве весов он предложил использовать физические объемы базисного периода.

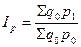«Индекс Ласпейреса» (9.18)

В 1874 г. другой немецкий ученый Г.Пааше предложил строить индекс цен по физическим объемам отчетного периода:

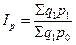«Индекс Пааше» (9.19)

На практике могут использоваться как один, так и другой. При этом индекс Ласпейреса показывает, во сколько бы раз товары базисного периода подорожали бы (или подешевели) из-за изменения цен на них в отчетном периоде (условная экономия или перерасход).

В нашем примере:

.

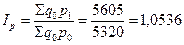В свою очередь индекс Пааше показывает во сколько раз товары в отчетном периоде стали дороже (дешевле), чем в базисном (фактическая экономия или перерасход):

.

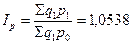В официальной статистике исчисление индекса цен осуществляется по индексу Пааше. Он нашел наибольшее распространение и на практике, т.к. наибольший интерес для исследователя представляет фактическое изменение цен, его фактическое влияние на стоимость, а не условное изменение товарооборота или стоимости продукции.

Впоследствии названия этих разных методов (с весами базисного периода и с весами отчетного периода) были механически распространены и на другие индексы, в т.ч. и на индекс физического объема. Т.е. он может исчисляться либо по формуле

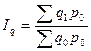(Ласпейреса) (9.20)

либо по формуле (Пааше). (9.21)

В первом случае I_q = 1,0658 ,

а во втором .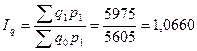

Общий подход: если в индексе использованы базисные веса – индекс построен по методу Ласпейреса;

Если в индексе использованы веса текущего периода – он построен по методу Пааше.

В начале 20 века американский экономист И.Фишер предложил в качестве формулы индекса цен среднюю геометрическую из произведения индексов Ласпейреса и Паше.

Индекс Фишера 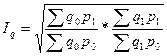. (9.22)

Его назвали идеальным. Однако он имеет недостаток: его трудно интерпретировать.