Средние индексы (средние арифметические и средние гармонические индексы)
Общие индексы могут быть вычислены не только как агрегатные, но и как средние из индивидуальных индексов. Для исчисления агрегатных индексов необходима информация об индексируемых[ величинах и весах в отчетном и базисном периодах. На практике часто приводится информация, в которой вместо этих данных приводятся данные об индивидуальных индексах. В этих случаях формой построения индекса становится средняя величина, причем в виде взвешенной, а рассчитанные индексы называют средними арифметическими или средними гармоническими.
Рассмотрим порядок их построения и условия применения.
1. Средний арифметический индекс физического объема.
Индекс физического объема в форме агрегатного:
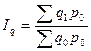 (9.23)
(9.23)
требует наличия информации о q1, q0, p0.
Если отсутствует информация о q1, но известны индивидуальные индексы физического объема iq, то построение среднего индекса основывается на рассуждениях:
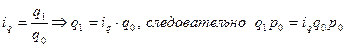 ,
,
а индекс физического объема:
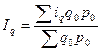 . (9.24)
. (9.24)
Проведём аналогию: iq = x; q0p0 = f.
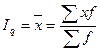 . (9.25)
. (9.25)
Следовательно, это средневзвешенная арифметическая величина из индивидуальных индексов физического объёма, в которой в качестве частот (весов) используются стоимости базисного периода.
Например, по имеющейся информации необходимо определить, как изменился выпуск (физический объём) продукции в целом по предприятию.
Таблица 9.2 – Расчет среднеарифметического индекса физического объема
| Изделие | Индивидуальный индекс объёма продукции | Стоимость продукции предыдущего периода | iqq0p0 |
| iq | q0p0 | ||
| А | 1,027 | ||
| Б | 1,065 | ||
| В | 1,112 | ||
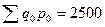
| 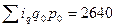
|
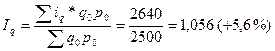
2. Средний гармонический индекс физического объёма.
Рассуждаем аналогично:
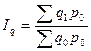 есть q1, p0, отсутствует q0, но есть и iq. (9.26)
есть q1, p0, отсутствует q0, но есть и iq. (9.26)
Тогда 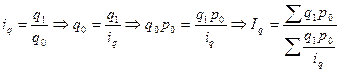 .
.
Если обозначить: iq = x, q1p0 = W, то
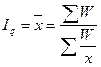 , то есть это средняя гармоническая величина.
, то есть это средняя гармоническая величина.
Таблица 9.3 – Расчет среднегармонического индекса физического объема
| Изделие | Индивидуальный индекс объёма продукции | Стоимость продукции отчетного периода в базисных ценах | 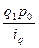
|
| iq = q1 / q0 | q1p0 | ||
| А | 1,027 | ||
| Б | 1,065 | ||
| В | 1,112 | ||
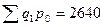
| 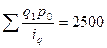
|
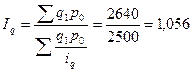
Аналогичным образом выводятся формулы средних индексов цен.
3. Средний арифметический индекс цен.
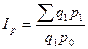 есть информация о q1, p0, отсутствует р1, но есть и ip,
есть информация о q1, p0, отсутствует р1, но есть и ip,
тогда 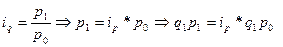 .
.
Индекс цен принимает вид:
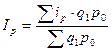 . (9.27)
. (9.27)
При обозначении 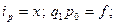 формула имеет вид:
формула имеет вид:
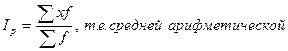 . (9.28)
. (9.28)
4. Средний гармонический индекс цен.
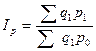 . (9.29)
. (9.29)
Имеется информация о q1, p1, iр, но отсутствует р0.
Тогда 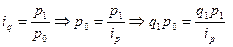 . (9.30)
. (9.30)
Формула индекса цен принимает вид : 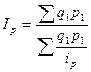 . При условии, что q1p1 = W, а ip = x, она трансформируется с формулу средней гармонической
. При условии, что q1p1 = W, а ip = x, она трансформируется с формулу средней гармонической 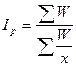 .
.
На практике по исходной информации важно правильно определить вид индекса, который необходимо исчислять для характеристики изменения показателя.
Например: по данным таблицы 9.4 необходимо определить, как в среднем изменились цены в отчётном периоде по сравнению с предыдущим и какова экономия (или перерасход) денежных средств у населения.
Таблица 9.4 – Расчет среднего индекса цен
| Вид товара | Товарооборот отчётного периода, млн. руб. | Индивидуальные индексы цен по группам товаров | 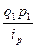
|
| q1p1 | 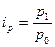
| ||
| А | 1,12 | ||
| Б | 1,05 | ||
| В | 0,98 | ||
| Г | 1,15 | ||
| Д | 1,08 | ||
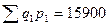
| 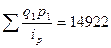
|
Введя условные обозначения, видим, что есть информация о q1p1 и ip. Следовательно, можно воспользоваться средним гармоническим индексом цен:
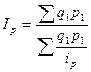 ; (9.31)
; (9.31)
т.е. 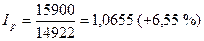
Перерасход денежных средств у населения:
15900 - 14992 = 978 млн. руб.
По форме средних индексов цен строятся известные во всём мире индексы ценных бумаг:
- индекс Доу-Джонса (Dow Jones Industrial Average Index). Это средний арифметический индекс значений курсов акций, котирующихся на Нью-Йоркской фондовой бирже. Один сводный и три групповых индекса рассчитываются через каждые три часа. Публикуются ежедневно их значения на момент закрытия биржи;
- индекс Стэндарда и Пура (Standart fnd Poor’s 500 Stock Index) − индекс рассчитываются по курсам акций 500 крупнейших компаний Нью-Йоркской фондовой биржи. Он рассчитывается как средне- взвешенный показатель, учитывающий общее количество выпущенных акций.
Дата добавления: 2016-01-16; просмотров: 2657;
