Арифметические и логические основы цифровой техники

Содержание лекции:введение основных понятий и определений цифровой техники, арифметика и кодирование двоичных чисел, основы алгебры логики.

Цели лекции:ознакомиться с основными понятиями и определениями цифровой техники, освоить правила перевода чисел из одной системы счисления в другую и двоичной арифметики, способы кодирования двоичных чисел, а также изучить аксиомы, основные законы и правила алгебры логики.

Информация, воплощенная в некоторой материальной форме, называется сообщением или сигналом. Сигналы могут носить аналоговый (непрерывный), либо дискретный (цифровой) характер, когда изменяемая величина (функция) может иметь место только при конкретных значениях времени. Цифровые сигналы состоят только из последовательности двух цифр 1 и 0, которые называют логическими, поскольку существует раздел математики, называемый алгеброй логики, задающей правила работы с такими двоичными сигналами. Методы обработки цифровых сигналов и соответствующие устройства и системы называются цифровыми или логическими. Существуют две формы представления цифровых сигналов: потенциальная и импульсная. В первом случае наибольшей физической величине, например, напряжению соответствует логическая 1, наименьшему – логический 0 (положительная логика), если все наоборот, то имеет место отрицательная логика. Во втором случае появление импульса в определенный момент времени соответствует логической 1, его отсутствие – логическому 0. Наибольшее распространение получили цифровые устройства, реализованные в виде цифровых микросхем, использующих потенциальную форму представления цифровых сигналов, в частности, положительную логику.

Цифровая техника использует двоичную систему счисления, так как обрабатывает числа, представленные только в двоичной форме. Однако, для сокращенной формы записи двоичных чисел в микропроцессорной технике применяют восьмеричную и шестнадцатеричную системы счисления.

Система счисления – это способ записи чисел цифровыми символами. Системы счисления делят на непозиционные и позиционные. В непозиционной системе счисления значение символа не зависит от его положения в числе, а в позиционных – зависит.

Любое число в любой системе счисления можно записать в виде следующего полинома

,

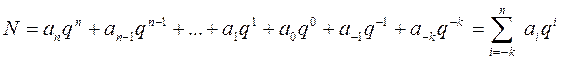где q – основание системы счисления; 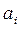- коэффициенты при степенях основания ( 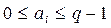); 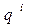- веса разрядов числа.

В двоичной системе счисления q = 2 и используются два коэффициента (1 и 0). Двоичное число 101101,101 можно представить в виде следующего полинома: .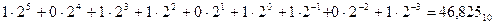

Двоичная арифметика очень проста. Основной арифметической операцией, которая используется в цифровых устройствах, является сложение, так как вычитание легко свести к сложению путем изменения на обратный знак вычитаемого, а умножение и деление - к операциям сложения и некоторых логических действий. Для арифметического сложения или вычитания двоичных чисел необходимо помнить, что две логические 1 не могут находиться в одном разряде, то есть они переходят в соседний старший разряд в качестве одной логической 1.

В восьмеричной системе счисления счисления q = 8 и используются восемь коэффициентов (0,1,2,3,4,5,6,7). Восьмеричное число 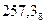можно представить в виде следующего полинома .

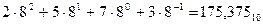В шестнадцатеричной системе счисления q = 16 и используются шестнадцать коэффициентов (цифры от 0 до 9 и буквы начала латинского алфавита A,B,C,D,E,F). Шестнадцатеричное число 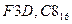можно представить полиномом .

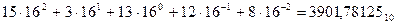Перевод дробного числа из десятичной в другую систему счисления осуществляется в два этапа:

1) переводится целая часть числа делением ее на основание системы счисления до остатка, меньшего этого основания, при этом полученное число записывается справа налево;

2) переводится дробная часть числа умножением ее на основание системы счисления до получения либо нулевого остатка после запятой, либо до заданной степени точности, при этом полученное число записывается слева от запятой сверху вниз. На рисунке 1 приведен пример перевода десятичного числа 45,75 в двоичное.

1) 45 2 2) 0,75

1 22 2 2

0112

1 5 2 1,50

1 2 2 2

0 1 1,00

Ответ:45,75₁₀ = 101101,11₂

Рисунок 1 – Пример перевода десятичного числа в двоичное

Для обратного перевода достаточно сложить веса единичных разрядов двоичного числа: .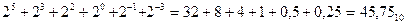

В таблице 1 представлен натуральный ряд десятичных чисел в порядке возрастания, которым соответствует свой двоичный эквивалент.

Т а б л и ц а 1

0

Продолжение таблицы 1

9								∙∙∙
								∙∙∙

Недостатки данного способа кодирования десятичных чисел:

а) для увеличения диапазона однозначности десятичных чисел нужно увеличивать разрядность устройств;

б) технически трудно реализовать переход от натурального кода к десятичной системе.

Этих недостатков лишена двоично-десятичная система кодирования, которая присваивает каждой десятичной цифре от 0 до 9 свой двоичный эквивалент в виде тетрады, то есть четырехразрядного двоичного числа. При таком способе кодирования, например, десятичное число 37 можно представить, согласно таблице 1, как 0011 0111. Таким образом, при двоично-десятичном кодировании сохраняется десятичная система счисления при двоичном форме представления десятичных чисел.

Математической базой для анализа и синтеза работы цифровых устройств служит алгебра логики, в основе которой лежат три логические функции: логическое сложение (дизъюнкция), логическое умножение (конъюнкция) и логическое отрицание (инверсия). На рисунке 2 представлены логические элементы ИЛИ,И,НЕ соответственно реализующие эти функции.

ИЛИ И НЕ

			х			Y

∙ ∙

∙ ∙

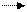
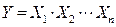
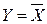
Рисунок 2 – Логические элементы основного базиса

При логическом сложении входных двоичных переменных выход всегда будет равен логической 1, если хотя бы на один вход логического элемента ИЛИ поступает логическая 1. На выходе будет логический 0, если на все входы поступают логические 0. При логическом умножении входных двоичных переменных выход всегда будет равен логическому 0, если хотя бы на один вход логического элемента И поступает логический 0. На выходе будет логическая 1, если на все входы поступают логические 1. При логическом отрицании выход логического элемента НЕ всегда инвертирует двоичное значение его входа. На практике большим применением пользуются комбинированные логические элементы ИЛИ-НЕ, И-НЕ, которые выполняют две логические функции: логическое сложение с отрицанием результата и логическое умножение с отрицанием результата соответственно. Логичесие элементы И,ИЛИ,НЕ составляют основной базис при построении логических устройств, а комбинированные логические элементы - универсальный базис.

Логическую функцию можно задать структурной формулой, то есть равенством, в левой части которого записана буква, обозначаюшая логическую функцию, а в правой – логическое выражение

Существуют две формы записи логических выражений: совершенная дизъюнктивная нормальная форма (СДНФ) и совершенная конъюнктивная нормальная форма (СКНФ).

СДНФ – это логическая сумма минтермов, на которых логическая функция равна единице. Минтерм – это логическое произведение входных переменных, преставленных с отрицанием или без него.

СКНФ – это логическое произведение макстермов, на которых логическая функция равна нулю. Макстерм – это логическая сумма входных преременных, представленных с отрицанием или без него.

При проектировании цифровых устройств часто требуется преобразовать структурные формулы. Для этого используют соотношения, вытекающие из аксиом и законов алгебры логики.

Рассмотрим аксиомы, справедливость которых можно подтвердить, используя правила логического сложения, умножения и инверсии.

Пусть 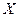- некоторая логическая переменная, тогда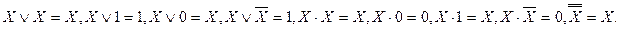

Для логических операций сложения и умножения справедливы переместительный и сочетательный законы. У распределительного закона только первая его часть ( правило раскрытия скобок) соответствует обычной алгебре, а вторая часть ( правило взятия в скобки) имеет место только в алгебре логики.

Рассмотрим некоторые правила алгебры логики, имеющие наибольшее практическое использование для преобразования структурных формул. Правило де Моргана 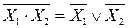и 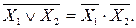Это правило позволяет заменить логическое умножение сложением и наоборот. Правило склеивания 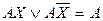и 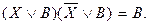На правиле склеивания основаны графические методы карт Карно или диаграмм Вейча для минимизации логических функций.